x-1-x-2-4x-5-2-dx-

Question Number 92055 by 675480065 last updated on 04/May/20

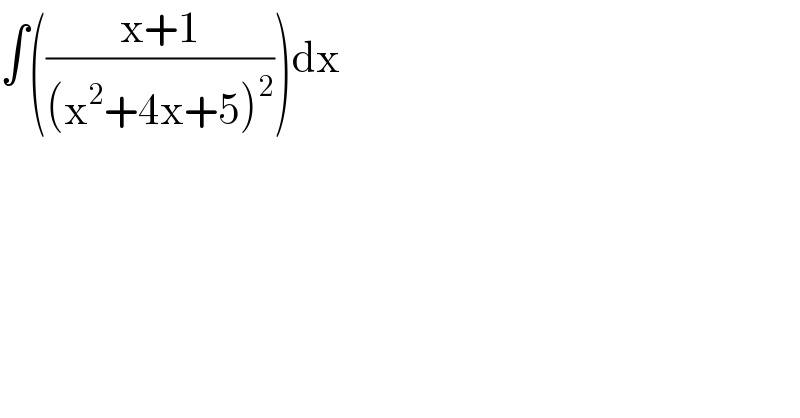
$$\int\left(\frac{\mathrm{x}+\mathrm{1}}{\left(\mathrm{x}^{\mathrm{2}} +\mathrm{4x}+\mathrm{5}\right)^{\mathrm{2}} }\right)\mathrm{dx} \\ $$

Commented by Prithwish Sen 1 last updated on 04/May/20

∫((x+1)/(((x+2)^2 +1)^2 ))dx changement x=x−2 ∫((x−1)/((x^2 +1)^2 )) dx = (1/2)∫((2x)/((x^2 +1)^2 ))dx−∫(dx/((x^2 +1)^2 )) =((−1)/(2(x^2 +1)))−(x/(2(1+x^2 )))−(1/2)tan^(−1) x+c =−(((x+3))/(2(x^2 +4x+5)))−(1/2)tan^(−1) (x+2)+c I just forgot to do the inverse transformation. thank you. please check.

$$\int\frac{\mathrm{x}+\mathrm{1}}{\left(\left(\mathrm{x}+\mathrm{2}\right)^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }\mathrm{dx}\:\mathrm{changement}\:\mathrm{x}=\mathrm{x}−\mathrm{2} \\ $$$$\int\frac{\mathrm{x}−\mathrm{1}}{\left(\mathrm{x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }\:\mathrm{dx}\:=\:\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\mathrm{2x}}{\left(\mathrm{x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }\mathrm{dx}−\int\frac{\mathrm{dx}}{\left(\mathrm{x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$=\frac{−\mathrm{1}}{\mathrm{2}\left(\mathrm{x}^{\mathrm{2}} +\mathrm{1}\right)}−\frac{\mathrm{x}}{\mathrm{2}\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)}−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{tan}^{−\mathrm{1}} \mathrm{x}+\mathrm{c} \\ $$$$=−\frac{\left(\mathrm{x}+\mathrm{3}\right)}{\mathrm{2}\left(\mathrm{x}^{\mathrm{2}} +\mathrm{4x}+\mathrm{5}\right)}−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{tan}^{−\mathrm{1}} \left(\mathrm{x}+\mathrm{2}\right)+\mathrm{c} \\ $$$$\mathrm{I}\:\mathrm{just}\:\mathrm{forgot}\:\mathrm{to}\:\mathrm{do}\:\mathrm{the}\:\mathrm{inverse}\:\mathrm{transformation}.\: \\ $$$$\mathrm{thank}\:\mathrm{you}.\:\boldsymbol{\mathrm{please}}\:\boldsymbol{\mathrm{check}}. \\ $$

Commented by 675480065 last updated on 04/May/20

$$\mathrm{i}\:\mathrm{dont}\:\mathrm{get}\:\mathrm{u} \\ $$

Commented by Prithwish Sen 1 last updated on 04/May/20

((x+1)/((x^2 +4x+5)^2 )) and ((x−1)/((x^2 +1)^2 )) are the same function only the function has been a horizontal shifting along x axis in the rightward direction. There should not be any impact on overall calculation.

$$\frac{\mathrm{x}+\mathrm{1}}{\left(\mathrm{x}^{\mathrm{2}} +\mathrm{4x}+\mathrm{5}\right)^{\mathrm{2}} }\:\:\mathrm{and}\:\frac{\mathrm{x}−\mathrm{1}}{\left(\mathrm{x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }\:\:\mathrm{are}\:\mathrm{the}\:\mathrm{same}\:\mathrm{function} \\ $$$$\mathrm{only}\:\mathrm{the}\:\mathrm{function}\:\mathrm{has}\:\mathrm{been}\:\mathrm{a}\:\mathrm{horizontal}\:\mathrm{shifting} \\ $$$$\mathrm{along}\:\mathrm{x}\:\mathrm{axis}\:\mathrm{in}\:\mathrm{the}\:\mathrm{rightward}\:\mathrm{direction}.\:\mathrm{There} \\ $$$$\mathrm{should}\:\mathrm{not}\:\mathrm{be}\:\mathrm{any}\:\mathrm{impact}\:\mathrm{on}\:\mathrm{overall}\:\mathrm{calculation}. \\ $$$$ \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply