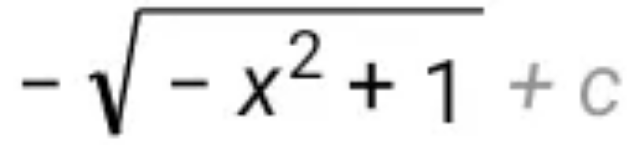Question Number 126520 by joki last updated on 21/Dec/20

$$\int\frac{\mathrm{x}}{\:\sqrt{\mathrm{1}−\mathrm{x}^{\mathrm{2}\:} \:\:}}\mathrm{dx} \\ $$
Answered by liberty last updated on 21/Dec/20
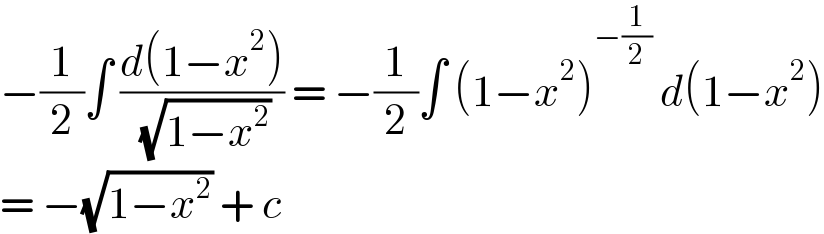
$$−\frac{\mathrm{1}}{\mathrm{2}}\int\:\frac{{d}\left(\mathrm{1}−{x}^{\mathrm{2}} \right)}{\:\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}\:=\:−\frac{\mathrm{1}}{\mathrm{2}}\int\:\left(\mathrm{1}−{x}^{\mathrm{2}} \right)^{−\frac{\mathrm{1}}{\mathrm{2}}} \:{d}\left(\mathrm{1}−{x}^{\mathrm{2}} \right) \\ $$$$=\:−\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }\:+\:{c} \\ $$
Answered by amns last updated on 21/Dec/20