Menu Close

x-1-x-2-x-1-dx-

Tinku Tara 0 Comments
Pin




Question Number 92025 by 675480065 last updated on 04/May/20
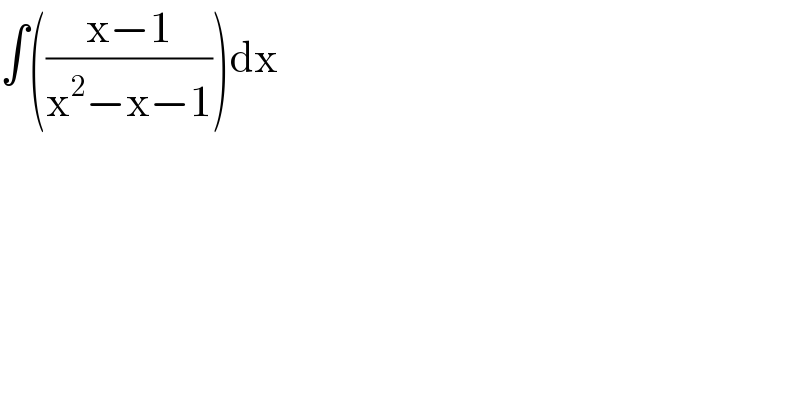
∫(((x−1)/(x^2 −x−1)))dx
$$\int\left(\frac{\mathrm{x}−\mathrm{1}}{\mathrm{x}^{\mathrm{2}} −\mathrm{x}−\mathrm{1}}\right)\mathrm{dx} \\ $$
Commented by mathmax by abdo last updated on 04/May/20
I =∫ ((x−1)/(x^2 −x−1))dx ⇒ I =(1/2)∫((2x−1−1)/(x^2 −x−1))dx =(1/2)∫ ((2x−1)/(x^2 −x−1))dx −(1/2)∫ (dx/(x^2 −x−1)) we have ∫ ((2x−1)/(x^2 −x−1))dx =ln∣x^2 −x−1∣ +c_0 x^2 −x−1=0→Δ =1+4 =5 ⇒x_1 =((1+(√5))/2) and x_2 =((1−(√5))/2) ⇒ ∫ (dx/(x^2 −x−1)) =∫(dx/((x−((1+(√5))/2))(x−((1−(√5))/2)))) =∫ (1/( (√5))) {(1/(x−((1+(√5))/2)))−(1/(x−((1−(√5))/2)))}dx =(1/( (√5)))ln∣((x−((1+(√5))/2))/(x−((1−(√5))/2)))∣ +c_1 =(1/( (√5)))ln∣((2x−1−(√5))/(2x−1+(√5)))∣ +c_1 ⇒ I =(1/2)ln∣x^2 −x−1∣−(1/(2(√5)))ln∣((2x−1−(√5))/(2x−1+(√5)))∣ +C
$${I}\:=\int\:\frac{{x}−\mathrm{1}}{{x}^{\mathrm{2}} −{x}−\mathrm{1}}{dx}\:\Rightarrow\:{I}\:=\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\mathrm{2}{x}−\mathrm{1}−\mathrm{1}}{{x}^{\mathrm{2}} −{x}−\mathrm{1}}{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int\:\frac{\mathrm{2}{x}−\mathrm{1}}{{x}^{\mathrm{2}} −{x}−\mathrm{1}}{dx}\:−\frac{\mathrm{1}}{\mathrm{2}}\int\:\frac{{dx}}{{x}^{\mathrm{2}} −{x}−\mathrm{1}}\:\:\:{we}\:{have} \\ $$$$\int\:\frac{\mathrm{2}{x}−\mathrm{1}}{{x}^{\mathrm{2}} −{x}−\mathrm{1}}{dx}\:={ln}\mid{x}^{\mathrm{2}} −{x}−\mathrm{1}\mid\:+{c}_{\mathrm{0}} \\ $$$${x}^{\mathrm{2}} −{x}−\mathrm{1}=\mathrm{0}\rightarrow\Delta\:=\mathrm{1}+\mathrm{4}\:=\mathrm{5}\:\Rightarrow{x}_{\mathrm{1}} =\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}\:\:{and}\:{x}_{\mathrm{2}} =\frac{\mathrm{1}−\sqrt{\mathrm{5}}}{\mathrm{2}}\:\Rightarrow \\ $$$$\int\:\:\frac{{dx}}{{x}^{\mathrm{2}} −{x}−\mathrm{1}}\:=\int\frac{{dx}}{\left({x}−\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}\right)\left({x}−\frac{\mathrm{1}−\sqrt{\mathrm{5}}}{\mathrm{2}}\right)} \\ $$$$=\int\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{5}}}\:\left\{\frac{\mathrm{1}}{{x}−\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}}−\frac{\mathrm{1}}{{x}−\frac{\mathrm{1}−\sqrt{\mathrm{5}}}{\mathrm{2}}}\right\}{dx} \\ $$$$=\frac{\mathrm{1}}{\:\sqrt{\mathrm{5}}}{ln}\mid\frac{{x}−\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}}{{x}−\frac{\mathrm{1}−\sqrt{\mathrm{5}}}{\mathrm{2}}}\mid\:+{c}_{\mathrm{1}} =\frac{\mathrm{1}}{\:\sqrt{\mathrm{5}}}{ln}\mid\frac{\mathrm{2}{x}−\mathrm{1}−\sqrt{\mathrm{5}}}{\mathrm{2}{x}−\mathrm{1}+\sqrt{\mathrm{5}}}\mid\:+{c}_{\mathrm{1}} \:\Rightarrow \\ $$$${I}\:=\frac{\mathrm{1}}{\mathrm{2}}{ln}\mid{x}^{\mathrm{2}} −{x}−\mathrm{1}\mid−\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{5}}}{ln}\mid\frac{\mathrm{2}{x}−\mathrm{1}−\sqrt{\mathrm{5}}}{\mathrm{2}{x}−\mathrm{1}+\sqrt{\mathrm{5}}}\mid\:+{C} \\ $$$$ \\ $$
Answered by niroj last updated on 04/May/20
∫ (( x−1)/(x^2 −x−1))dx= (1/2)∫ ((2x−1−1)/(x^2 −x−1))dx = (1/2)∫ ((2x−1)/(x^2 −x−1))dx−(1/2)∫ (( 1)/(x^2 −x−1))dx = (1/2)log (x^2 −x−1)+ (1/2)∫ (( 1)/(x^2 −2x.(1/2)+(1/4)−(1/4)−1))dx +C = log (x^2 −x−1)^(1/2) +(1/2) ∫ (( 1)/((x−(1/2))^2 −(((√5)/2))^2 ))dx+C = log(√(x^2 −x−1)) + (1/2)[ (1/(2.((√5)/2)))log ((x−(1/2) −((√5)/2))/(x−(1/2) +((√5)/2)))]+C = log(√(x^2 −x−1)) +(1/(2(√5)))log ((2x−1−(√5))/(2x−1+(√5))) +C = log(√(x^2 −x−1)) + ((√5)/(10))log ((2x−1−(√5))/(2x−1+(√5))) +C //.
$$\:\int\:\frac{\:\mathrm{x}−\mathrm{1}}{\mathrm{x}^{\mathrm{2}} −\mathrm{x}−\mathrm{1}}\mathrm{dx}=\:\frac{\mathrm{1}}{\mathrm{2}}\int\:\frac{\mathrm{2x}−\mathrm{1}−\mathrm{1}}{\mathrm{x}^{\mathrm{2}} −\mathrm{x}−\mathrm{1}}\mathrm{dx} \\ $$$$=\:\frac{\mathrm{1}}{\mathrm{2}}\int\:\frac{\mathrm{2x}−\mathrm{1}}{\mathrm{x}^{\mathrm{2}} −\mathrm{x}−\mathrm{1}}\mathrm{dx}−\frac{\mathrm{1}}{\mathrm{2}}\int\:\frac{\:\:\mathrm{1}}{\mathrm{x}^{\mathrm{2}} −\mathrm{x}−\mathrm{1}}\mathrm{dx} \\ $$$$=\:\frac{\mathrm{1}}{\mathrm{2}}\mathrm{log}\:\left(\mathrm{x}^{\mathrm{2}} −\mathrm{x}−\mathrm{1}\right)+\:\frac{\mathrm{1}}{\mathrm{2}}\int\:\frac{\:\mathrm{1}}{\mathrm{x}^{\mathrm{2}} −\mathrm{2x}.\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{4}}−\frac{\mathrm{1}}{\mathrm{4}}−\mathrm{1}}\mathrm{dx}\:+\mathrm{C} \\ $$$$\:=\:\mathrm{log}\:\left(\mathrm{x}^{\mathrm{2}} −\mathrm{x}−\mathrm{1}\right)^{\frac{\mathrm{1}}{\mathrm{2}}} \:+\frac{\mathrm{1}}{\mathrm{2}}\:\int\:\frac{\:\mathrm{1}}{\left(\mathrm{x}−\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} −\left(\frac{\sqrt{\mathrm{5}}}{\mathrm{2}}\right)^{\mathrm{2}} }\mathrm{dx}+\mathrm{C} \\ $$$$\:=\:\mathrm{log}\sqrt{\mathrm{x}^{\mathrm{2}} −\mathrm{x}−\mathrm{1}}\:\:+\:\frac{\mathrm{1}}{\mathrm{2}}\left[\:\frac{\mathrm{1}}{\mathrm{2}.\frac{\sqrt{\mathrm{5}}}{\mathrm{2}}}\mathrm{log}\:\frac{\mathrm{x}−\frac{\mathrm{1}}{\mathrm{2}}\:−\frac{\sqrt{\mathrm{5}}}{\mathrm{2}}}{\mathrm{x}−\frac{\mathrm{1}}{\mathrm{2}}\:+\frac{\sqrt{\mathrm{5}}}{\mathrm{2}}}\right]+\mathrm{C} \\ $$$$=\:\mathrm{log}\sqrt{\mathrm{x}^{\mathrm{2}} −\mathrm{x}−\mathrm{1}}\:\:\:+\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{5}}}\mathrm{log}\:\frac{\mathrm{2x}−\mathrm{1}−\sqrt{\mathrm{5}}}{\mathrm{2x}−\mathrm{1}+\sqrt{\mathrm{5}}}\:+\mathrm{C} \\ $$$$=\:\mathrm{log}\sqrt{\mathrm{x}^{\mathrm{2}} −\mathrm{x}−\mathrm{1}}\:\:+\:\frac{\sqrt{\mathrm{5}}}{\mathrm{10}}\mathrm{log}\:\frac{\mathrm{2x}−\mathrm{1}−\sqrt{\mathrm{5}}}{\mathrm{2x}−\mathrm{1}+\sqrt{\mathrm{5}}}\:+\mathrm{C}\://. \\ $$$$ \\ $$
Answered by MJS last updated on 04/May/20
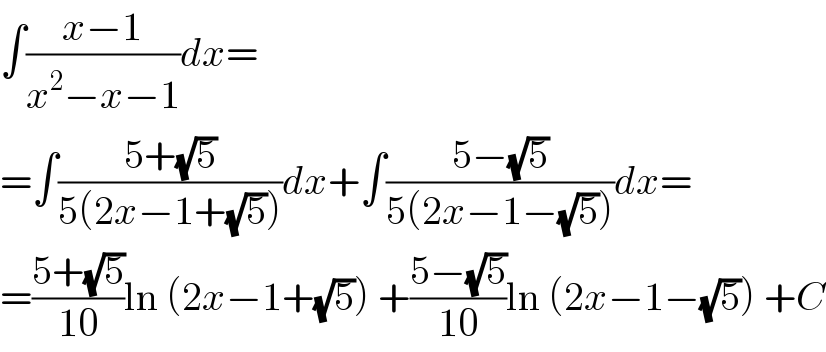
∫((x−1)/(x^2 −x−1))dx= =∫((5+(√5))/(5(2x−1+(√5))))dx+∫((5−(√5))/(5(2x−1−(√5))))dx= =((5+(√5))/(10))ln (2x−1+(√5)) +((5−(√5))/(10))ln (2x−1−(√5)) +C
$$\int\frac{{x}−\mathrm{1}}{{x}^{\mathrm{2}} −{x}−\mathrm{1}}{dx}= \\ $$$$=\int\frac{\mathrm{5}+\sqrt{\mathrm{5}}}{\mathrm{5}\left(\mathrm{2}{x}−\mathrm{1}+\sqrt{\mathrm{5}}\right)}{dx}+\int\frac{\mathrm{5}−\sqrt{\mathrm{5}}}{\mathrm{5}\left(\mathrm{2}{x}−\mathrm{1}−\sqrt{\mathrm{5}}\right)}{dx}= \\ $$$$=\frac{\mathrm{5}+\sqrt{\mathrm{5}}}{\mathrm{10}}\mathrm{ln}\:\left(\mathrm{2}{x}−\mathrm{1}+\sqrt{\mathrm{5}}\right)\:+\frac{\mathrm{5}−\sqrt{\mathrm{5}}}{\mathrm{10}}\mathrm{ln}\:\left(\mathrm{2}{x}−\mathrm{1}−\sqrt{\mathrm{5}}\right)\:+{C} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *