Question Number 79147 by jagoll last updated on 23/Jan/20
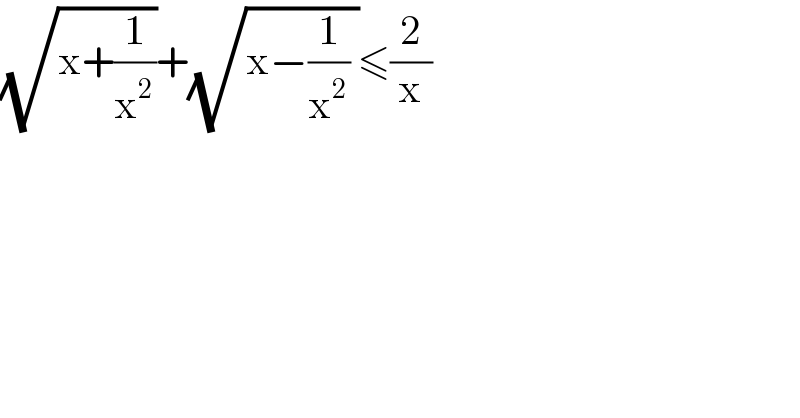
$$\sqrt{\mathrm{x}+\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }}+\sqrt{\mathrm{x}−\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }\:}\leqslant\frac{\mathrm{2}}{\mathrm{x}} \\ $$
Answered by john santu last updated on 23/Jan/20
![(√((x^3 +1)/x^2 ))+(√((x^3 −1)/x^2 ))≤(2/x) (i)x≥−1 ∧x≥1∧x≠0 (ii) (((√(x^3 +1))+(√(x^3 −1)))/x)≤(2/x) ⇒(√(x^3 +1))+(√(x^3 −1))≤2 let x^3 =t⇒(√(t+1))+(√(t−1)) ≤2 2t+2(√(t^2 −1))≤4 (√(t^2 −1)) ≤2−t⇒t^2 −1≤4−4t+t^2 4t≤5 ⇒t≤(5/4) ⇒x^3 ≤(5/4) x≤((5/4))^(1/(3 )) . now we get solution x≥1 ∧x≤((5/4))^(1/(3 )) ⇒ x∈[1,((5/4))^(1/(3 )) ]](https://www.tinkutara.com/question/Q79148.png)
$$\sqrt{\frac{{x}^{\mathrm{3}} +\mathrm{1}}{{x}^{\mathrm{2}} }}+\sqrt{\frac{{x}^{\mathrm{3}} −\mathrm{1}}{{x}^{\mathrm{2}} }}\leqslant\frac{\mathrm{2}}{{x}} \\ $$$$\left({i}\right){x}\geqslant−\mathrm{1}\:\wedge{x}\geqslant\mathrm{1}\wedge{x}\neq\mathrm{0} \\ $$$$\left({ii}\right)\:\frac{\sqrt{{x}^{\mathrm{3}} +\mathrm{1}}+\sqrt{{x}^{\mathrm{3}} −\mathrm{1}}}{{x}}\leqslant\frac{\mathrm{2}}{{x}}\: \\ $$$$\Rightarrow\sqrt{{x}^{\mathrm{3}} +\mathrm{1}}+\sqrt{{x}^{\mathrm{3}} −\mathrm{1}}\leqslant\mathrm{2} \\ $$$${let}\:{x}^{\mathrm{3}} ={t}\Rightarrow\sqrt{{t}+\mathrm{1}}+\sqrt{{t}−\mathrm{1}}\:\leqslant\mathrm{2} \\ $$$$\mathrm{2}{t}+\mathrm{2}\sqrt{{t}^{\mathrm{2}} −\mathrm{1}}\leqslant\mathrm{4} \\ $$$$\sqrt{{t}^{\mathrm{2}} −\mathrm{1}}\:\leqslant\mathrm{2}−{t}\Rightarrow{t}^{\mathrm{2}} −\mathrm{1}\leqslant\mathrm{4}−\mathrm{4}{t}+{t}^{\mathrm{2}} \\ $$$$\mathrm{4}{t}\leqslant\mathrm{5}\:\Rightarrow{t}\leqslant\frac{\mathrm{5}}{\mathrm{4}}\:\Rightarrow{x}^{\mathrm{3}} \leqslant\frac{\mathrm{5}}{\mathrm{4}} \\ $$$${x}\leqslant\sqrt[{\mathrm{3}\:}]{\frac{\mathrm{5}}{\mathrm{4}}}.\:{now}\:{we}\:{get}\:{solution} \\ $$$${x}\geqslant\mathrm{1}\:\wedge{x}\leqslant\sqrt[{\mathrm{3}\:}]{\frac{\mathrm{5}}{\mathrm{4}}}\:\Rightarrow\:{x}\in\left[\mathrm{1},\sqrt[{\mathrm{3}\:}]{\frac{\mathrm{5}}{\mathrm{4}}}\right] \\ $$$$ \\ $$
Commented by jagoll last updated on 23/Jan/20

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{sir}.\:\mathrm{your}\:\mathrm{solution}\:\mathrm{is} \\ $$$$\mathrm{fantastic} \\ $$
Commented by jagoll last updated on 23/Jan/20

$$\mathrm{good}\:\mathrm{sir} \\ $$
Commented by MJS last updated on 23/Jan/20
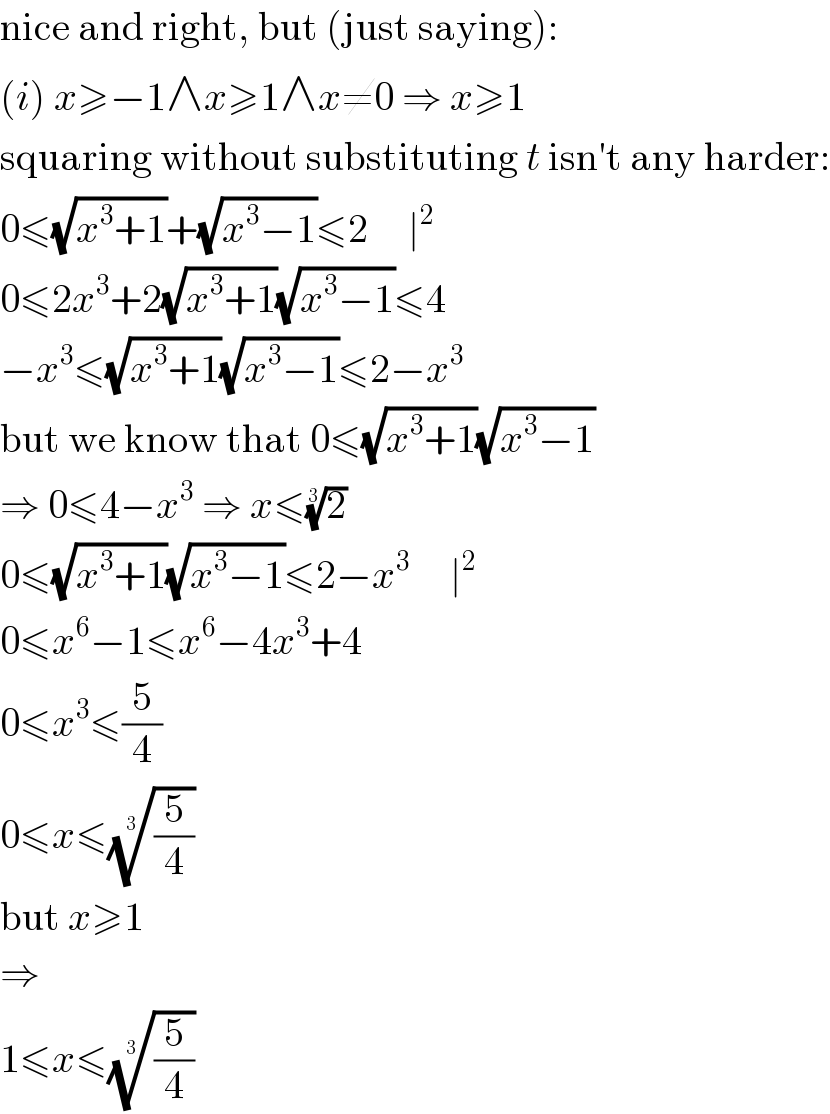
$$\mathrm{nice}\:\mathrm{and}\:\mathrm{right},\:\mathrm{but}\:\left(\mathrm{just}\:\mathrm{saying}\right): \\ $$$$\left({i}\right)\:{x}\geqslant−\mathrm{1}\wedge{x}\geqslant\mathrm{1}\wedge{x}\neq\mathrm{0}\:\Rightarrow\:{x}\geqslant\mathrm{1} \\ $$$$\mathrm{squaring}\:\mathrm{without}\:\mathrm{substituting}\:{t}\:\mathrm{isn}'\mathrm{t}\:\mathrm{any}\:\mathrm{harder}: \\ $$$$\mathrm{0}\leqslant\sqrt{{x}^{\mathrm{3}} +\mathrm{1}}+\sqrt{{x}^{\mathrm{3}} −\mathrm{1}}\leqslant\mathrm{2}\:\:\:\:\:\mid^{\mathrm{2}} \\ $$$$\mathrm{0}\leqslant\mathrm{2}{x}^{\mathrm{3}} +\mathrm{2}\sqrt{{x}^{\mathrm{3}} +\mathrm{1}}\sqrt{{x}^{\mathrm{3}} −\mathrm{1}}\leqslant\mathrm{4} \\ $$$$−{x}^{\mathrm{3}} \leqslant\sqrt{{x}^{\mathrm{3}} +\mathrm{1}}\sqrt{{x}^{\mathrm{3}} −\mathrm{1}}\leqslant\mathrm{2}−{x}^{\mathrm{3}} \\ $$$$\mathrm{but}\:\mathrm{we}\:\mathrm{know}\:\mathrm{that}\:\mathrm{0}\leqslant\sqrt{{x}^{\mathrm{3}} +\mathrm{1}}\sqrt{{x}^{\mathrm{3}} −\mathrm{1}} \\ $$$$\Rightarrow\:\mathrm{0}\leqslant\mathrm{4}−{x}^{\mathrm{3}} \:\Rightarrow\:{x}\leqslant\sqrt[{\mathrm{3}}]{\mathrm{2}} \\ $$$$\mathrm{0}\leqslant\sqrt{{x}^{\mathrm{3}} +\mathrm{1}}\sqrt{{x}^{\mathrm{3}} −\mathrm{1}}\leqslant\mathrm{2}−{x}^{\mathrm{3}} \:\:\:\:\:\mid^{\mathrm{2}} \\ $$$$\mathrm{0}\leqslant{x}^{\mathrm{6}} −\mathrm{1}\leqslant{x}^{\mathrm{6}} −\mathrm{4}{x}^{\mathrm{3}} +\mathrm{4} \\ $$$$\mathrm{0}\leqslant{x}^{\mathrm{3}} \leqslant\frac{\mathrm{5}}{\mathrm{4}} \\ $$$$\mathrm{0}\leqslant{x}\leqslant\sqrt[{\mathrm{3}}]{\frac{\mathrm{5}}{\mathrm{4}}} \\ $$$$\mathrm{but}\:{x}\geqslant\mathrm{1} \\ $$$$\Rightarrow \\ $$$$\mathrm{1}\leqslant{x}\leqslant\sqrt[{\mathrm{3}}]{\frac{\mathrm{5}}{\mathrm{4}}} \\ $$
Commented by john santu last updated on 23/Jan/20
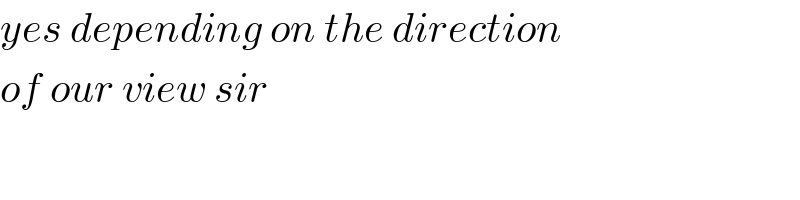
$${yes}\:{depending}\:{on}\:{the}\:{direction} \\ $$$${of}\:{our}\:{view}\:{sir} \\ $$
