x-1-x-2-x-12-

Question Number 151999 by otchereabdullai@gmail.com last updated on 24/Aug/21

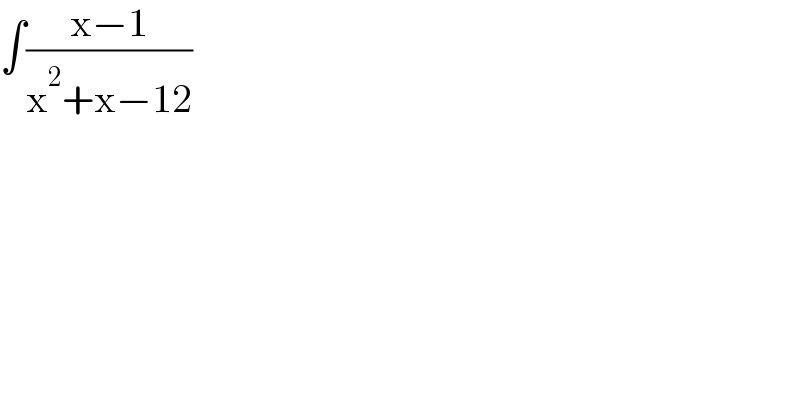
$$\int\frac{\mathrm{x}−\mathrm{1}}{\mathrm{x}^{\mathrm{2}} +\mathrm{x}−\mathrm{12}} \\ $$

Answered by Olaf_Thorendsen last updated on 25/Aug/21

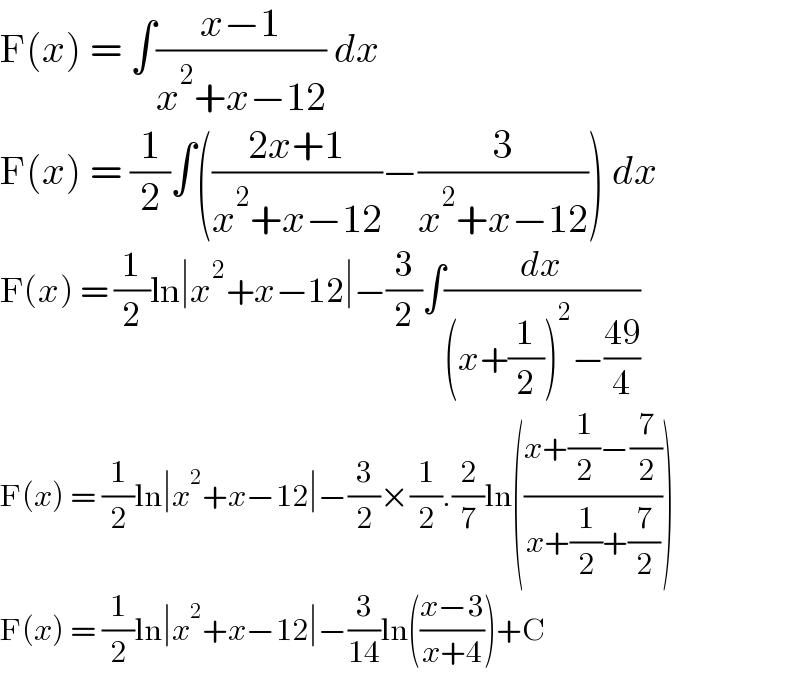
F(x) = ∫((x−1)/(x^2 +x−12)) dx F(x) = (1/2)∫(((2x+1)/(x^2 +x−12))−(3/(x^2 +x−12))) dx F(x) = (1/2)ln∣x^2 +x−12∣−(3/2)∫(dx/((x+(1/2))^2 −((49)/4))) F(x) = (1/2)ln∣x^2 +x−12∣−(3/2)×(1/2).(2/7)ln(((x+(1/2)−(7/2))/(x+(1/2)+(7/2)))) F(x) = (1/2)ln∣x^2 +x−12∣−(3/(14))ln(((x−3)/(x+4)))+C

$$\mathrm{F}\left({x}\right)\:=\:\int\frac{{x}−\mathrm{1}}{{x}^{\mathrm{2}} +{x}−\mathrm{12}}\:{dx} \\ $$$$\mathrm{F}\left({x}\right)\:=\:\frac{\mathrm{1}}{\mathrm{2}}\int\left(\frac{\mathrm{2}{x}+\mathrm{1}}{{x}^{\mathrm{2}} +{x}−\mathrm{12}}−\frac{\mathrm{3}}{{x}^{\mathrm{2}} +{x}−\mathrm{12}}\right)\:{dx} \\ $$$$\mathrm{F}\left({x}\right)\:=\:\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\mid{x}^{\mathrm{2}} +{x}−\mathrm{12}\mid−\frac{\mathrm{3}}{\mathrm{2}}\int\frac{{dx}}{\left({x}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} −\frac{\mathrm{49}}{\mathrm{4}}} \\ $$$$\mathrm{F}\left({x}\right)\:=\:\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\mid{x}^{\mathrm{2}} +{x}−\mathrm{12}\mid−\frac{\mathrm{3}}{\mathrm{2}}×\frac{\mathrm{1}}{\mathrm{2}}.\frac{\mathrm{2}}{\mathrm{7}}\mathrm{ln}\left(\frac{{x}+\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{7}}{\mathrm{2}}}{{x}+\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{7}}{\mathrm{2}}}\right) \\ $$$$\mathrm{F}\left({x}\right)\:=\:\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\mid{x}^{\mathrm{2}} +{x}−\mathrm{12}\mid−\frac{\mathrm{3}}{\mathrm{14}}\mathrm{ln}\left(\frac{{x}−\mathrm{3}}{{x}+\mathrm{4}}\right)+\mathrm{C} \\ $$

Commented by otchereabdullai@gmail.com last updated on 25/Aug/21

$$\mathrm{Thanks}\:\mathrm{a}\:\mathrm{lot}\:\mathrm{sir}!\:\mathrm{Am}\:\mathrm{much}\:\mathrm{grateful} \\ $$

Answered by puissant last updated on 25/Aug/21

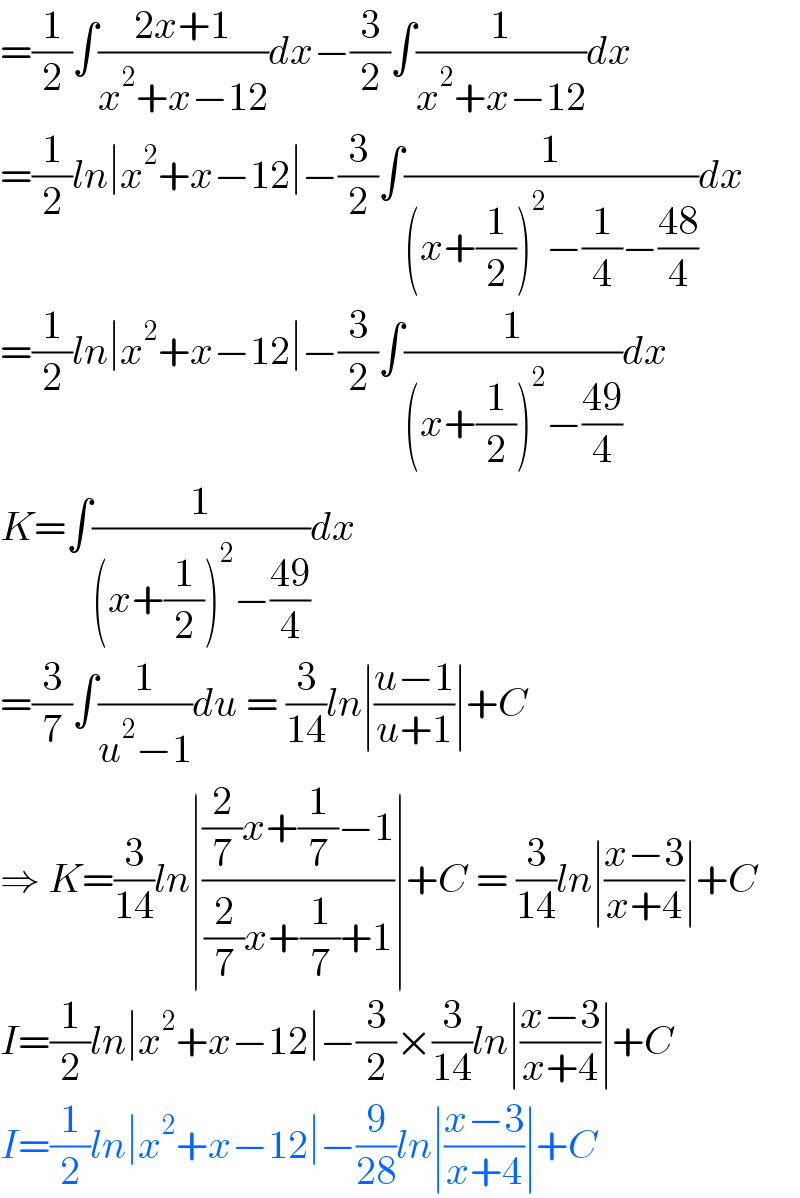
=(1/2)∫((2x+1)/(x^2 +x−12))dx−(3/2)∫(1/(x^2 +x−12))dx =(1/2)ln∣x^2 +x−12∣−(3/2)∫(1/((x+(1/2))^2 −(1/4)−((48)/4)))dx =(1/2)ln∣x^2 +x−12∣−(3/2)∫(1/((x+(1/2))^2 −((49)/4)))dx K=∫(1/((x+(1/2))^2 −((49)/4)))dx =(3/7)∫(1/(u^2 −1))du = (3/(14))ln∣((u−1)/(u+1))∣+C ⇒ K=(3/(14))ln∣(((2/7)x+(1/7)−1)/((2/7)x+(1/7)+1))∣+C = (3/(14))ln∣((x−3)/(x+4))∣+C I=(1/2)ln∣x^2 +x−12∣−(3/2)×(3/(14))ln∣((x−3)/(x+4))∣+C I=(1/2)ln∣x^2 +x−12∣−(9/(28))ln∣((x−3)/(x+4))∣+C

$$=\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\mathrm{2}{x}+\mathrm{1}}{{x}^{\mathrm{2}} +{x}−\mathrm{12}}{dx}−\frac{\mathrm{3}}{\mathrm{2}}\int\frac{\mathrm{1}}{{x}^{\mathrm{2}} +{x}−\mathrm{12}}{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}{ln}\mid{x}^{\mathrm{2}} +{x}−\mathrm{12}\mid−\frac{\mathrm{3}}{\mathrm{2}}\int\frac{\mathrm{1}}{\left({x}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{4}}−\frac{\mathrm{48}}{\mathrm{4}}}{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}{ln}\mid{x}^{\mathrm{2}} +{x}−\mathrm{12}\mid−\frac{\mathrm{3}}{\mathrm{2}}\int\frac{\mathrm{1}}{\left({x}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} −\frac{\mathrm{49}}{\mathrm{4}}}{dx} \\ $$$${K}=\int\frac{\mathrm{1}}{\left({x}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} −\frac{\mathrm{49}}{\mathrm{4}}}{dx} \\ $$$$=\frac{\mathrm{3}}{\mathrm{7}}\int\frac{\mathrm{1}}{{u}^{\mathrm{2}} −\mathrm{1}}{du}\:=\:\frac{\mathrm{3}}{\mathrm{14}}{ln}\mid\frac{{u}−\mathrm{1}}{{u}+\mathrm{1}}\mid+{C} \\ $$$$\Rightarrow\:{K}=\frac{\mathrm{3}}{\mathrm{14}}{ln}\mid\frac{\frac{\mathrm{2}}{\mathrm{7}}{x}+\frac{\mathrm{1}}{\mathrm{7}}−\mathrm{1}}{\frac{\mathrm{2}}{\mathrm{7}}{x}+\frac{\mathrm{1}}{\mathrm{7}}+\mathrm{1}}\mid+{C}\:=\:\frac{\mathrm{3}}{\mathrm{14}}{ln}\mid\frac{{x}−\mathrm{3}}{{x}+\mathrm{4}}\mid+{C} \\ $$$${I}=\frac{\mathrm{1}}{\mathrm{2}}{ln}\mid{x}^{\mathrm{2}} +{x}−\mathrm{12}\mid−\frac{\mathrm{3}}{\mathrm{2}}×\frac{\mathrm{3}}{\mathrm{14}}{ln}\mid\frac{{x}−\mathrm{3}}{{x}+\mathrm{4}}\mid+{C} \\ $$$${I}=\frac{\mathrm{1}}{\mathrm{2}}{ln}\mid{x}^{\mathrm{2}} +{x}−\mathrm{12}\mid−\frac{\mathrm{9}}{\mathrm{28}}{ln}\mid\frac{{x}−\mathrm{3}}{{x}+\mathrm{4}}\mid+{C} \\ $$

Commented by otchereabdullai@gmail.com last updated on 25/Aug/21

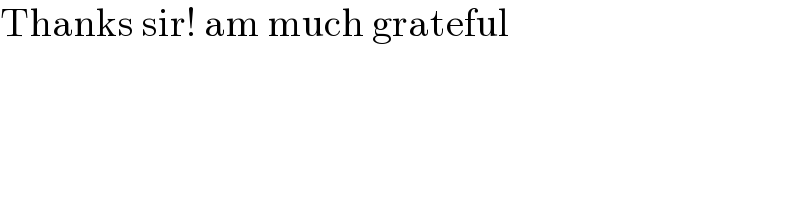
$$\mathrm{Thanks}\:\mathrm{sir}!\:\mathrm{am}\:\mathrm{much}\:\mathrm{grateful} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply