Question Number 128888 by bemath last updated on 11/Jan/21
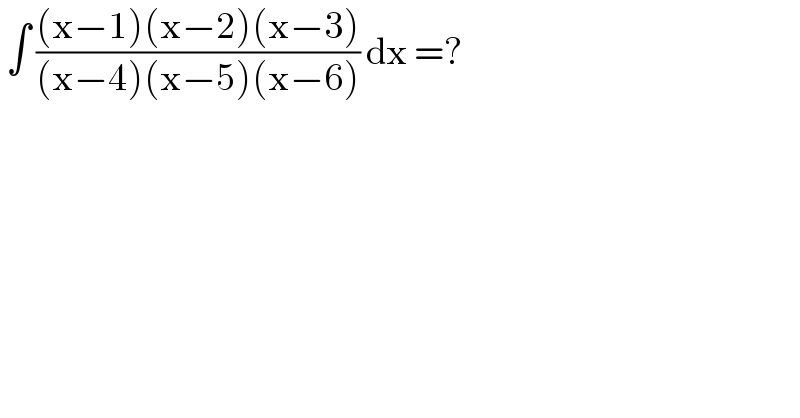
$$\:\int\:\frac{\left(\mathrm{x}−\mathrm{1}\right)\left(\mathrm{x}−\mathrm{2}\right)\left(\mathrm{x}−\mathrm{3}\right)}{\left(\mathrm{x}−\mathrm{4}\right)\left(\mathrm{x}−\mathrm{5}\right)\left(\mathrm{x}−\mathrm{6}\right)}\:\mathrm{dx}\:=? \\ $$
Answered by Olaf last updated on 11/Jan/21
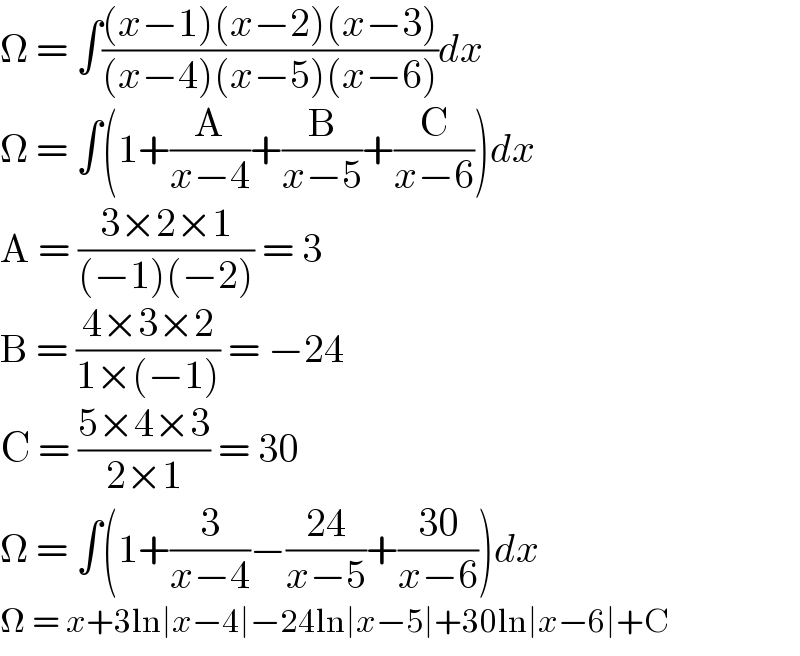
$$\Omega\:=\:\int\frac{\left({x}−\mathrm{1}\right)\left({x}−\mathrm{2}\right)\left({x}−\mathrm{3}\right)}{\left({x}−\mathrm{4}\right)\left({x}−\mathrm{5}\right)\left({x}−\mathrm{6}\right)}{dx} \\ $$$$\Omega\:=\:\int\left(\mathrm{1}+\frac{\mathrm{A}}{{x}−\mathrm{4}}+\frac{\mathrm{B}}{{x}−\mathrm{5}}+\frac{\mathrm{C}}{{x}−\mathrm{6}}\right){dx} \\ $$$$\mathrm{A}\:=\:\frac{\mathrm{3}×\mathrm{2}×\mathrm{1}}{\left(−\mathrm{1}\right)\left(−\mathrm{2}\right)}\:=\:\mathrm{3} \\ $$$$\mathrm{B}\:=\:\frac{\mathrm{4}×\mathrm{3}×\mathrm{2}}{\mathrm{1}×\left(−\mathrm{1}\right)}\:=\:−\mathrm{24} \\ $$$$\mathrm{C}\:=\:\frac{\mathrm{5}×\mathrm{4}×\mathrm{3}}{\mathrm{2}×\mathrm{1}}\:=\:\mathrm{30} \\ $$$$\Omega\:=\:\int\left(\mathrm{1}+\frac{\mathrm{3}}{{x}−\mathrm{4}}−\frac{\mathrm{24}}{{x}−\mathrm{5}}+\frac{\mathrm{30}}{{x}−\mathrm{6}}\right){dx} \\ $$$$\Omega\:=\:{x}+\mathrm{3ln}\mid{x}−\mathrm{4}\mid−\mathrm{24ln}\mid{x}−\mathrm{5}\mid+\mathrm{30ln}\mid{x}−\mathrm{6}\mid+\mathrm{C} \\ $$
