Question Number 83960 by john santu last updated on 08/Mar/20
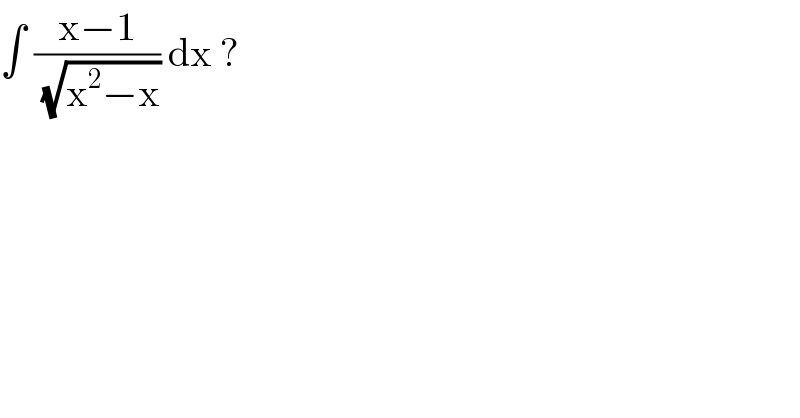
$$\int\:\frac{\mathrm{x}−\mathrm{1}}{\:\sqrt{\mathrm{x}^{\mathrm{2}} −\mathrm{x}}}\:\mathrm{dx}\:?\: \\ $$
Commented by mathmax by abdo last updated on 08/Mar/20
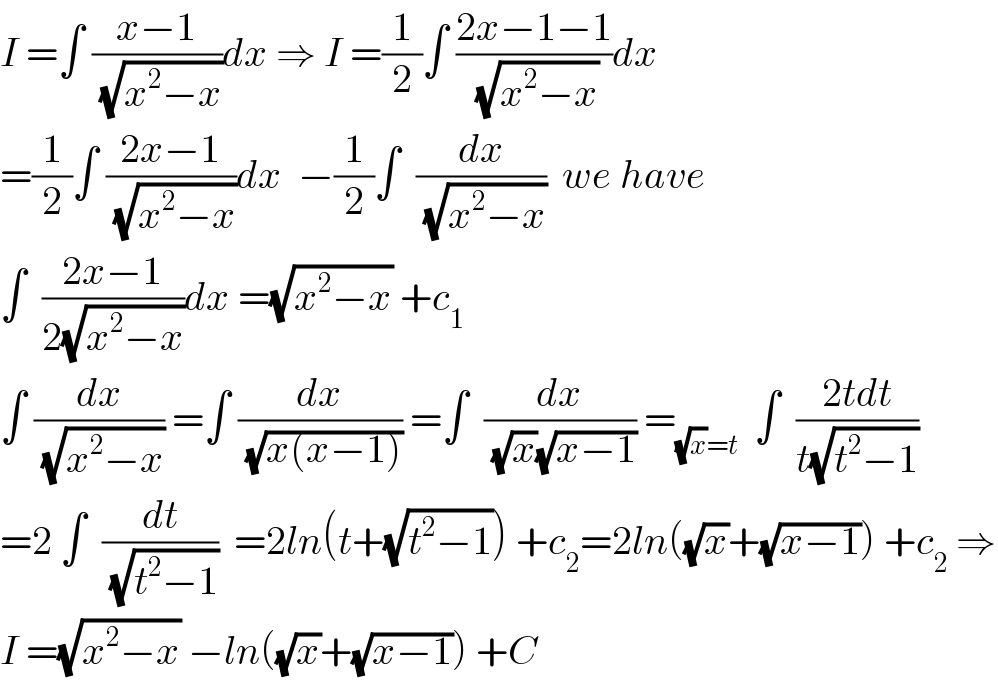
$${I}\:=\int\:\frac{{x}−\mathrm{1}}{\:\sqrt{{x}^{\mathrm{2}} −{x}}}{dx}\:\Rightarrow\:{I}\:=\frac{\mathrm{1}}{\mathrm{2}}\int\:\frac{\mathrm{2}{x}−\mathrm{1}−\mathrm{1}}{\:\sqrt{{x}^{\mathrm{2}} −{x}}}{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int\:\frac{\mathrm{2}{x}−\mathrm{1}}{\:\sqrt{{x}^{\mathrm{2}} −{x}}}{dx}\:\:−\frac{\mathrm{1}}{\mathrm{2}}\int\:\:\frac{{dx}}{\:\sqrt{{x}^{\mathrm{2}} −{x}}}\:\:{we}\:{have} \\ $$$$\int\:\:\frac{\mathrm{2}{x}−\mathrm{1}}{\mathrm{2}\sqrt{{x}^{\mathrm{2}} −{x}}}{dx}\:=\sqrt{{x}^{\mathrm{2}} −{x}}\:+{c}_{\mathrm{1}} \\ $$$$\int\:\frac{{dx}}{\:\sqrt{{x}^{\mathrm{2}} −{x}}}\:=\int\:\frac{{dx}}{\:\sqrt{{x}\left({x}−\mathrm{1}\right)}}\:=\int\:\:\frac{{dx}}{\:\sqrt{{x}}\sqrt{{x}−\mathrm{1}}}\:=_{\sqrt{{x}}={t}} \:\:\int\:\:\frac{\mathrm{2}{tdt}}{{t}\sqrt{{t}^{\mathrm{2}} −\mathrm{1}}} \\ $$$$=\mathrm{2}\:\int\:\:\frac{{dt}}{\:\sqrt{{t}^{\mathrm{2}} −\mathrm{1}}}\:\:=\mathrm{2}{ln}\left({t}+\sqrt{{t}^{\mathrm{2}} −\mathrm{1}}\right)\:+{c}_{\mathrm{2}} =\mathrm{2}{ln}\left(\sqrt{{x}}+\sqrt{{x}−\mathrm{1}}\right)\:+{c}_{\mathrm{2}} \:\Rightarrow \\ $$$${I}\:=\sqrt{{x}^{\mathrm{2}} −{x}}\:−{ln}\left(\sqrt{{x}}+\sqrt{{x}−\mathrm{1}}\right)\:+{C} \\ $$
Answered by john santu last updated on 08/Mar/20
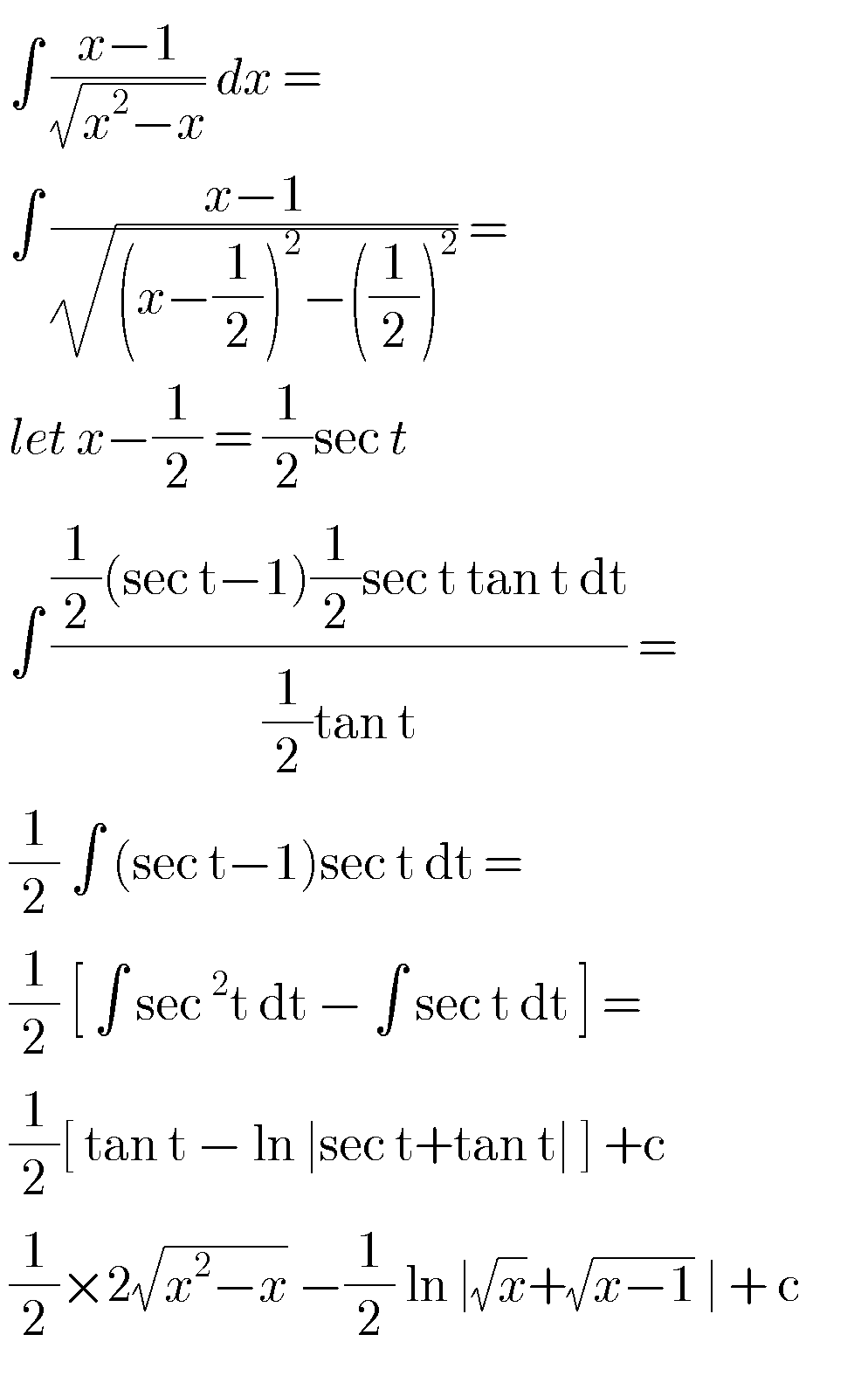
Answered by Kunal12588 last updated on 08/Mar/20
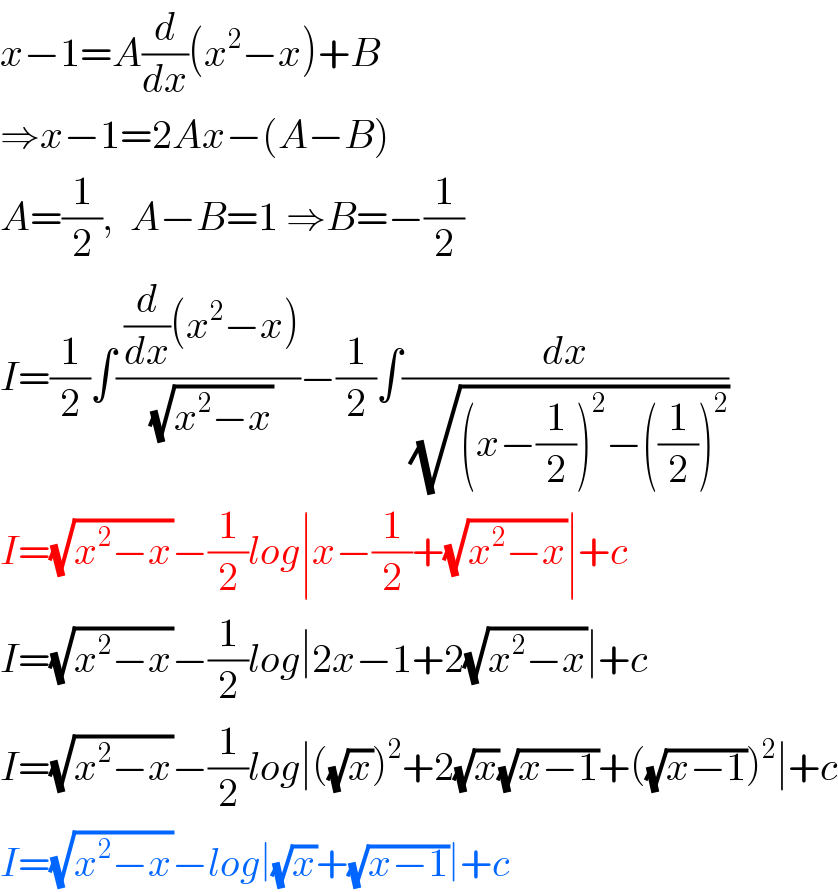
$${x}−\mathrm{1}={A}\frac{{d}}{{dx}}\left({x}^{\mathrm{2}} −{x}\right)+{B} \\ $$$$\Rightarrow{x}−\mathrm{1}=\mathrm{2}{Ax}−\left({A}−{B}\right) \\ $$$${A}=\frac{\mathrm{1}}{\mathrm{2}},\:\:{A}−{B}=\mathrm{1}\:\Rightarrow{B}=−\frac{\mathrm{1}}{\mathrm{2}} \\ $$$${I}=\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\:\frac{{d}}{{dx}}\left({x}^{\mathrm{2}} −{x}\right)}{\:\sqrt{{x}^{\mathrm{2}} −{x}}}−\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{dx}}{\:\sqrt{\left({x}−\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} −\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} }} \\ $$$${I}=\sqrt{{x}^{\mathrm{2}} −{x}}−\frac{\mathrm{1}}{\mathrm{2}}{log}\mid{x}−\frac{\mathrm{1}}{\mathrm{2}}+\sqrt{{x}^{\mathrm{2}} −{x}}\mid+{c} \\ $$$${I}=\sqrt{{x}^{\mathrm{2}} −{x}}−\frac{\mathrm{1}}{\mathrm{2}}{log}\mid\mathrm{2}{x}−\mathrm{1}+\mathrm{2}\sqrt{{x}^{\mathrm{2}} −{x}}\mid+{c} \\ $$$${I}=\sqrt{{x}^{\mathrm{2}} −{x}}−\frac{\mathrm{1}}{\mathrm{2}}{log}\mid\left(\sqrt{{x}}\right)^{\mathrm{2}} +\mathrm{2}\sqrt{{x}}\sqrt{{x}−\mathrm{1}}+\left(\sqrt{{x}−\mathrm{1}}\right)^{\mathrm{2}} \mid+{c} \\ $$$${I}=\sqrt{{x}^{\mathrm{2}} −{x}}−{log}\mid\sqrt{{x}}+\sqrt{{x}−\mathrm{1}}\mid+{c} \\ $$
