Question Number 116590 by bemath last updated on 05/Oct/20
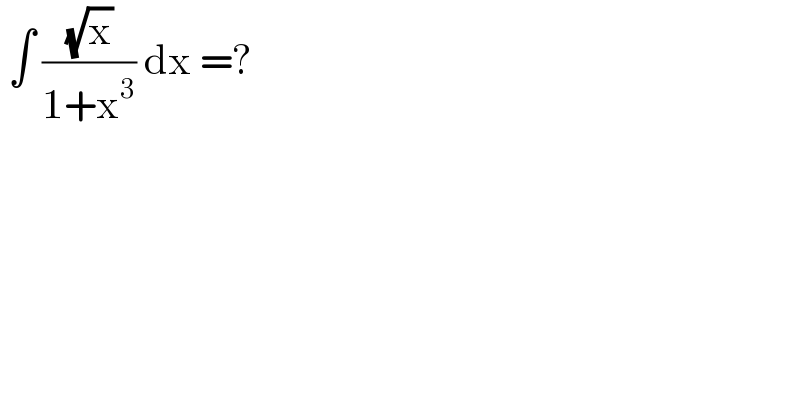
$$\:\int\:\frac{\sqrt{\mathrm{x}}}{\mathrm{1}+\mathrm{x}^{\mathrm{3}} }\:\mathrm{dx}\:=? \\ $$
Answered by Olaf last updated on 05/Oct/20
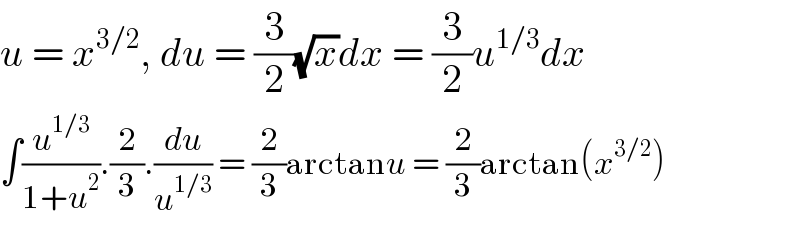
$${u}\:=\:{x}^{\mathrm{3}/\mathrm{2}} ,\:{du}\:=\:\frac{\mathrm{3}}{\mathrm{2}}\sqrt{{x}}{dx}\:=\:\frac{\mathrm{3}}{\mathrm{2}}{u}^{\mathrm{1}/\mathrm{3}} {dx} \\ $$$$\int\frac{{u}^{\mathrm{1}/\mathrm{3}} }{\mathrm{1}+{u}^{\mathrm{2}} }.\frac{\mathrm{2}}{\mathrm{3}}.\frac{{du}}{{u}^{\mathrm{1}/\mathrm{3}} }\:=\:\frac{\mathrm{2}}{\mathrm{3}}\mathrm{arctan}{u}\:=\:\frac{\mathrm{2}}{\mathrm{3}}\mathrm{arctan}\left({x}^{\mathrm{3}/\mathrm{2}} \right) \\ $$
Commented by bemath last updated on 05/Oct/20

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{sir} \\ $$
Answered by Dwaipayan Shikari last updated on 05/Oct/20
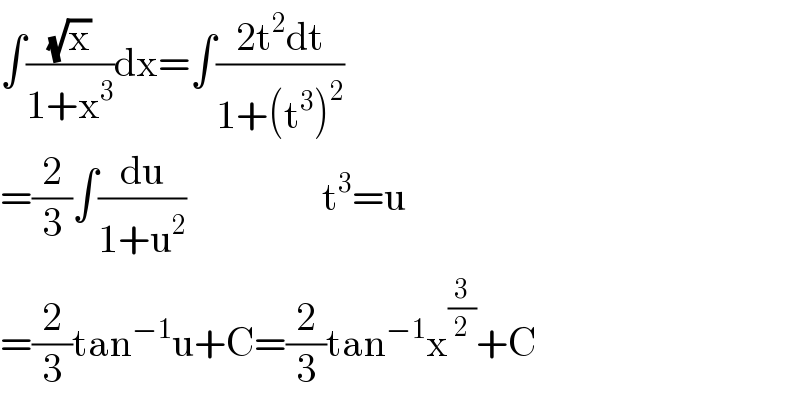
$$\int\frac{\sqrt{\mathrm{x}}}{\mathrm{1}+\mathrm{x}^{\mathrm{3}} }\mathrm{dx}=\int\frac{\mathrm{2t}^{\mathrm{2}} \mathrm{dt}}{\mathrm{1}+\left(\mathrm{t}^{\mathrm{3}} \right)^{\mathrm{2}} } \\ $$$$=\frac{\mathrm{2}}{\mathrm{3}}\int\frac{\mathrm{du}}{\mathrm{1}+\mathrm{u}^{\mathrm{2}} }\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{t}^{\mathrm{3}} =\mathrm{u} \\ $$$$=\frac{\mathrm{2}}{\mathrm{3}}\mathrm{tan}^{−\mathrm{1}} \mathrm{u}+\mathrm{C}=\frac{\mathrm{2}}{\mathrm{3}}\mathrm{tan}^{−\mathrm{1}} \mathrm{x}^{\frac{\mathrm{3}}{\mathrm{2}}} +\mathrm{C} \\ $$
