Question Number 28143 by ktomboy1992 last updated on 21/Jan/18

$$\mathrm{x}−\frac{\mathrm{1}}{\mathrm{x}}=\mathrm{3} \\ $$$$\mathrm{x}^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }=? \\ $$
Answered by mrW2 last updated on 21/Jan/18
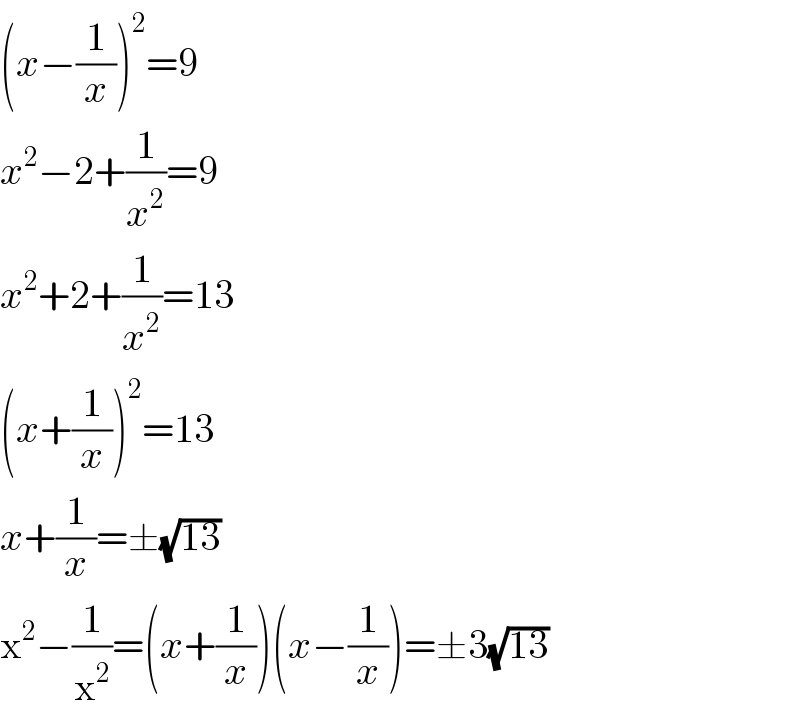
$$\left({x}−\frac{\mathrm{1}}{{x}}\right)^{\mathrm{2}} =\mathrm{9} \\ $$$${x}^{\mathrm{2}} −\mathrm{2}+\frac{\mathrm{1}}{{x}^{\mathrm{2}} }=\mathrm{9} \\ $$$${x}^{\mathrm{2}} +\mathrm{2}+\frac{\mathrm{1}}{{x}^{\mathrm{2}} }=\mathrm{13} \\ $$$$\left({x}+\frac{\mathrm{1}}{{x}}\right)^{\mathrm{2}} =\mathrm{13} \\ $$$${x}+\frac{\mathrm{1}}{{x}}=\pm\sqrt{\mathrm{13}} \\ $$$$\mathrm{x}^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }=\left({x}+\frac{\mathrm{1}}{{x}}\right)\left({x}−\frac{\mathrm{1}}{{x}}\right)=\pm\mathrm{3}\sqrt{\mathrm{13}} \\ $$
