x-1-x-3-x-3579-1-x-3579-

Question Number 163631 by HongKing last updated on 08/Jan/22

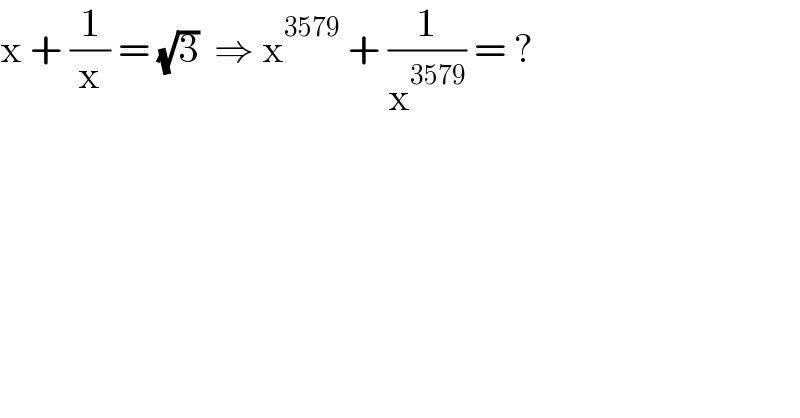
$$\mathrm{x}\:+\:\frac{\mathrm{1}}{\mathrm{x}}\:=\:\sqrt{\mathrm{3}}\:\:\Rightarrow\:\mathrm{x}^{\mathrm{3579}} \:+\:\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{3579}} }\:=\:? \\ $$

Answered by MathsFan last updated on 09/Jan/22

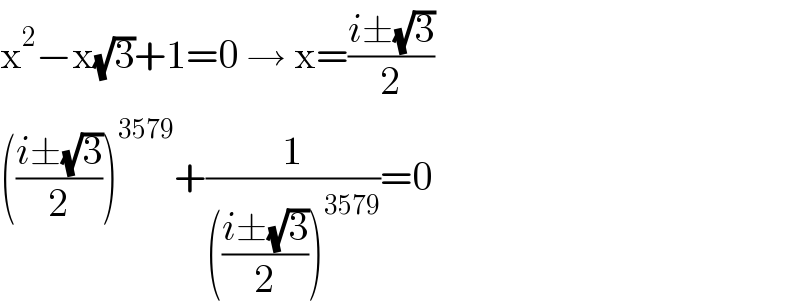
x^2 −x(√3)+1=0 → x=((i±(√3))/2) (((i±(√3))/2))^(3579) +(1/((((i±(√3))/2))^(3579) ))=0

$$\mathrm{x}^{\mathrm{2}} −\mathrm{x}\sqrt{\mathrm{3}}+\mathrm{1}=\mathrm{0}\:\rightarrow\:\mathrm{x}=\frac{{i}\pm\sqrt{\mathrm{3}}}{\mathrm{2}} \\ $$$$\left(\frac{{i}\pm\sqrt{\mathrm{3}}}{\mathrm{2}}\right)^{\mathrm{3579}} +\frac{\mathrm{1}}{\left(\frac{{i}\pm\sqrt{\mathrm{3}}}{\mathrm{2}}\right)^{\mathrm{3579}} }=\mathrm{0} \\ $$

Commented by behi834171 last updated on 09/Jan/22

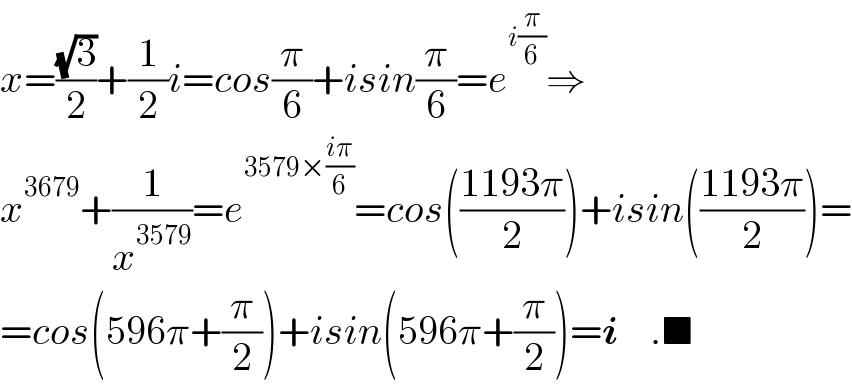
x=((√3)/2)+(1/2)i=cos(π/6)+isin(π/6)=e^(i(π/6)) ⇒ x^(3679) +(1/x^(3579) )=e^(3579×((iπ)/6)) =cos(((1193π)/2))+isin(((1193π)/2))= =cos(596π+(π/2))+isin(596π+(π/2))=i .■

$${x}=\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}}{i}={cos}\frac{\pi}{\mathrm{6}}+{isin}\frac{\pi}{\mathrm{6}}={e}^{{i}\frac{\pi}{\mathrm{6}}} \Rightarrow \\ $$$${x}^{\mathrm{3679}} +\frac{\mathrm{1}}{{x}^{\mathrm{3579}} }={e}^{\mathrm{3579}×\frac{{i}\pi}{\mathrm{6}}} ={cos}\left(\frac{\mathrm{1193}\pi}{\mathrm{2}}\right)+{isin}\left(\frac{\mathrm{1193}\pi}{\mathrm{2}}\right)= \\ $$$$={cos}\left(\mathrm{596}\pi+\frac{\pi}{\mathrm{2}}\right)+{isin}\left(\mathrm{596}\pi+\frac{\pi}{\mathrm{2}}\right)=\boldsymbol{{i}}\:\:\:\:.\blacksquare \\ $$

Answered by mr W last updated on 09/Jan/22

x^2 −(√3)x+1=0 x=(((√3)±i)/2)=cos (±(π/6))+i sin (±(π/6)) x^(3579) +(1/x^(3579) )=cos (±((3579π)/6))+i sin (±((3579π)/6))+cos (∓((3579π)/6))+i sin (∓((3579π)/6)) x^(3579) +(1/x^(3579) )=cos (±((3579π)/6))+i sin (±((3579π)/6))+cos (±((3579π)/6))−i sin (±((3579π)/6)) x^(3579) +(1/x^(3579) )=2 cos (((3579π)/6)) x^(3579) +(1/x^(3579) )=2 cos (298×2π+(π/2)) x^(3579) +(1/x^(3579) )=2 cos ((π/2)) x^(3579) +(1/x^(3579) )=2×0 x^(3579) +(1/x^(3579) )=0

$${x}^{\mathrm{2}} −\sqrt{\mathrm{3}}{x}+\mathrm{1}=\mathrm{0} \\ $$$${x}=\frac{\sqrt{\mathrm{3}}\pm{i}}{\mathrm{2}}=\mathrm{cos}\:\left(\pm\frac{\pi}{\mathrm{6}}\right)+{i}\:\mathrm{sin}\:\left(\pm\frac{\pi}{\mathrm{6}}\right) \\ $$$$ \\ $$$${x}^{\mathrm{3579}} +\frac{\mathrm{1}}{{x}^{\mathrm{3579}} }=\mathrm{cos}\:\left(\pm\frac{\mathrm{3579}\pi}{\mathrm{6}}\right)+{i}\:\mathrm{sin}\:\left(\pm\frac{\mathrm{3579}\pi}{\mathrm{6}}\right)+\mathrm{cos}\:\left(\mp\frac{\mathrm{3579}\pi}{\mathrm{6}}\right)+{i}\:\mathrm{sin}\:\left(\mp\frac{\mathrm{3579}\pi}{\mathrm{6}}\right) \\ $$$${x}^{\mathrm{3579}} +\frac{\mathrm{1}}{{x}^{\mathrm{3579}} }=\mathrm{cos}\:\left(\pm\frac{\mathrm{3579}\pi}{\mathrm{6}}\right)+{i}\:\mathrm{sin}\:\left(\pm\frac{\mathrm{3579}\pi}{\mathrm{6}}\right)+\mathrm{cos}\:\left(\pm\frac{\mathrm{3579}\pi}{\mathrm{6}}\right)−{i}\:\mathrm{sin}\:\left(\pm\frac{\mathrm{3579}\pi}{\mathrm{6}}\right) \\ $$$${x}^{\mathrm{3579}} +\frac{\mathrm{1}}{{x}^{\mathrm{3579}} }=\mathrm{2}\:\mathrm{cos}\:\left(\frac{\mathrm{3579}\pi}{\mathrm{6}}\right) \\ $$$${x}^{\mathrm{3579}} +\frac{\mathrm{1}}{{x}^{\mathrm{3579}} }=\mathrm{2}\:\mathrm{cos}\:\left(\mathrm{298}×\mathrm{2}\pi+\frac{\pi}{\mathrm{2}}\right) \\ $$$${x}^{\mathrm{3579}} +\frac{\mathrm{1}}{{x}^{\mathrm{3579}} }=\mathrm{2}\:\mathrm{cos}\:\left(\frac{\pi}{\mathrm{2}}\right) \\ $$$${x}^{\mathrm{3579}} +\frac{\mathrm{1}}{{x}^{\mathrm{3579}} }=\mathrm{2}×\mathrm{0} \\ $$$${x}^{\mathrm{3579}} +\frac{\mathrm{1}}{{x}^{\mathrm{3579}} }=\mathrm{0} \\ $$

Commented by HongKing last updated on 09/Jan/22

$$\mathrm{cool}\:\mathrm{my}\:\mathrm{dear}\:\mathrm{Sir}\:\mathrm{thank}\:\mathrm{you}\:\mathrm{so}\:\mathrm{much} \\ $$

Commented by peter frank last updated on 11/Jan/22

$$\mathrm{thank}\:\mathrm{you} \\ $$

Facebook Tweet Pin

x-1-x-3-x-3579-1-x-3579-

Leave a Reply Cancel reply