Question Number 78880 by naka3546 last updated on 21/Jan/20
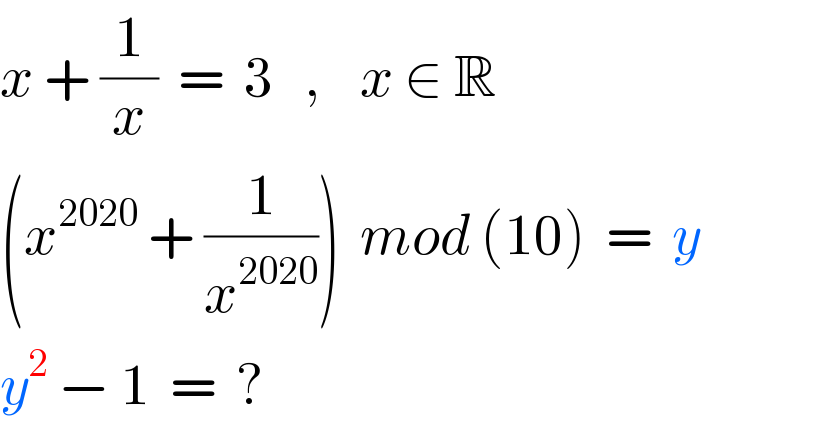
$${x}\:+\:\frac{\mathrm{1}}{{x}}\:\:=\:\:\mathrm{3}\:\:\:,\:\:\:\:{x}\:\in\:\mathbb{R} \\ $$$$\left({x}^{\mathrm{2020}} \:+\:\frac{\mathrm{1}}{{x}^{\mathrm{2020}} }\right)\:\:{mod}\:\left(\mathrm{10}\right)\:\:=\:\:{y} \\ $$$${y}^{\mathrm{2}} \:−\:\mathrm{1}\:\:=\:\:? \\ $$
Answered by mind is power last updated on 21/Jan/20
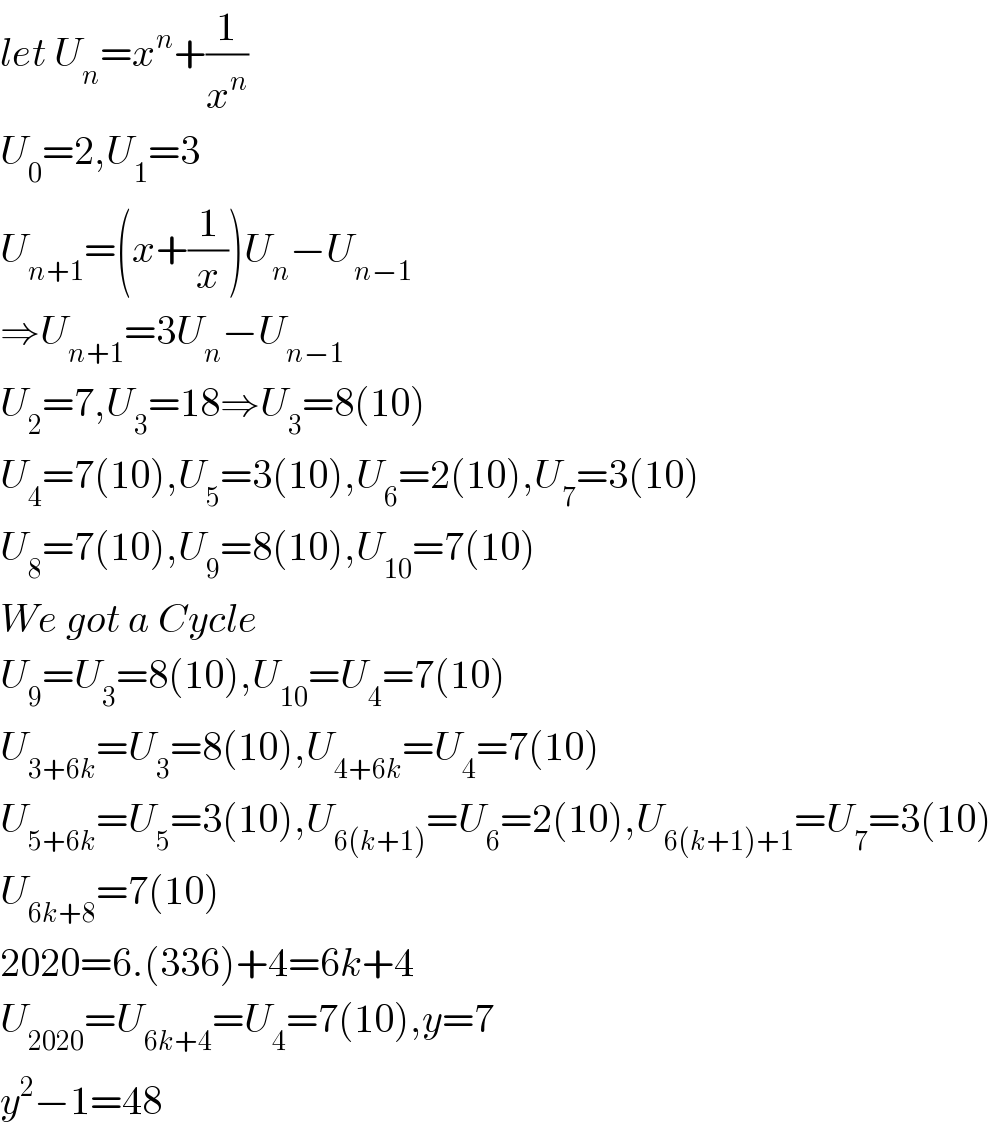
$${let}\:{U}_{{n}} ={x}^{{n}} +\frac{\mathrm{1}}{{x}^{{n}} } \\ $$$${U}_{\mathrm{0}} =\mathrm{2},{U}_{\mathrm{1}} =\mathrm{3} \\ $$$${U}_{{n}+\mathrm{1}} =\left({x}+\frac{\mathrm{1}}{{x}}\right){U}_{{n}} −{U}_{{n}−\mathrm{1}} \\ $$$$\Rightarrow{U}_{{n}+\mathrm{1}} =\mathrm{3}{U}_{{n}} −{U}_{{n}−\mathrm{1}} \\ $$$${U}_{\mathrm{2}} =\mathrm{7},{U}_{\mathrm{3}} =\mathrm{18}\Rightarrow{U}_{\mathrm{3}} =\mathrm{8}\left(\mathrm{10}\right) \\ $$$${U}_{\mathrm{4}} =\mathrm{7}\left(\mathrm{10}\right),{U}_{\mathrm{5}} =\mathrm{3}\left(\mathrm{10}\right),{U}_{\mathrm{6}} =\mathrm{2}\left(\mathrm{10}\right),{U}_{\mathrm{7}} =\mathrm{3}\left(\mathrm{10}\right) \\ $$$${U}_{\mathrm{8}} =\mathrm{7}\left(\mathrm{10}\right),{U}_{\mathrm{9}} =\mathrm{8}\left(\mathrm{10}\right),{U}_{\mathrm{10}} =\mathrm{7}\left(\mathrm{10}\right) \\ $$$${We}\:{got}\:{a}\:{Cycle} \\ $$$${U}_{\mathrm{9}} ={U}_{\mathrm{3}} =\mathrm{8}\left(\mathrm{10}\right),{U}_{\mathrm{10}} ={U}_{\mathrm{4}} =\mathrm{7}\left(\mathrm{10}\right) \\ $$$${U}_{\mathrm{3}+\mathrm{6}{k}} ={U}_{\mathrm{3}} =\mathrm{8}\left(\mathrm{10}\right),{U}_{\mathrm{4}+\mathrm{6}{k}} ={U}_{\mathrm{4}} =\mathrm{7}\left(\mathrm{10}\right) \\ $$$${U}_{\mathrm{5}+\mathrm{6}{k}} ={U}_{\mathrm{5}} =\mathrm{3}\left(\mathrm{10}\right),{U}_{\mathrm{6}\left({k}+\mathrm{1}\right)} ={U}_{\mathrm{6}} =\mathrm{2}\left(\mathrm{10}\right),{U}_{\mathrm{6}\left({k}+\mathrm{1}\right)+\mathrm{1}} ={U}_{\mathrm{7}} =\mathrm{3}\left(\mathrm{10}\right) \\ $$$${U}_{\mathrm{6}{k}+\mathrm{8}} =\mathrm{7}\left(\mathrm{10}\right) \\ $$$$\mathrm{2020}=\mathrm{6}.\left(\mathrm{336}\right)+\mathrm{4}=\mathrm{6}{k}+\mathrm{4} \\ $$$${U}_{\mathrm{2020}} ={U}_{\mathrm{6}{k}+\mathrm{4}} ={U}_{\mathrm{4}} =\mathrm{7}\left(\mathrm{10}\right),{y}=\mathrm{7} \\ $$$${y}^{\mathrm{2}} −\mathrm{1}=\mathrm{48} \\ $$
