Menu Close

x-1-x-4-dx-

Tinku Tara 0 Comments
Pin




Question Number 125346 by john_santu last updated on 10/Dec/20
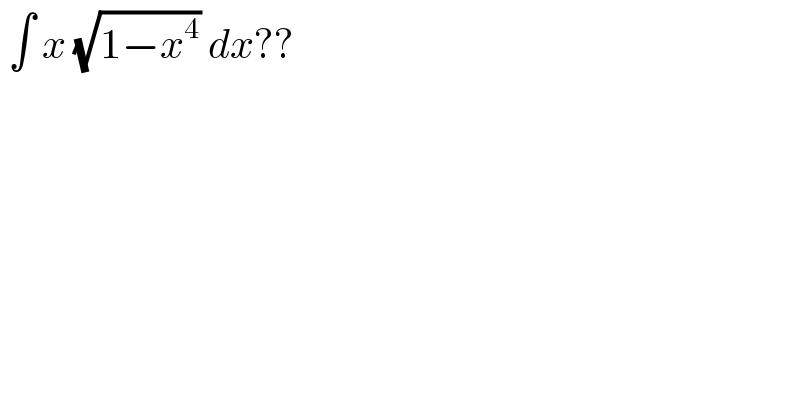
∫ x (√(1−x^4 )) dx??
$$\:\int\:{x}\:\sqrt{\mathrm{1}−{x}^{\mathrm{4}} }\:{dx}?? \\ $$
Commented by AdeyemiAdebola last updated on 10/Dec/20
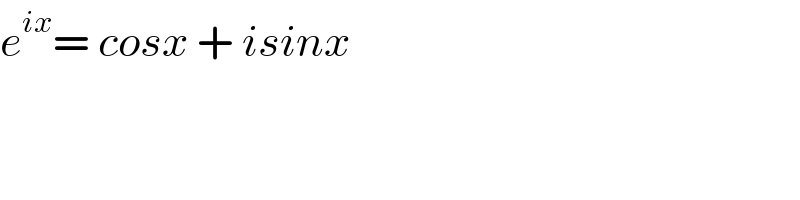
e^(ix) = cosx + isinx
$${e}^{{ix}} =\:{cosx}\:+\:{isinx} \\ $$
Answered by bemath last updated on 10/Dec/20
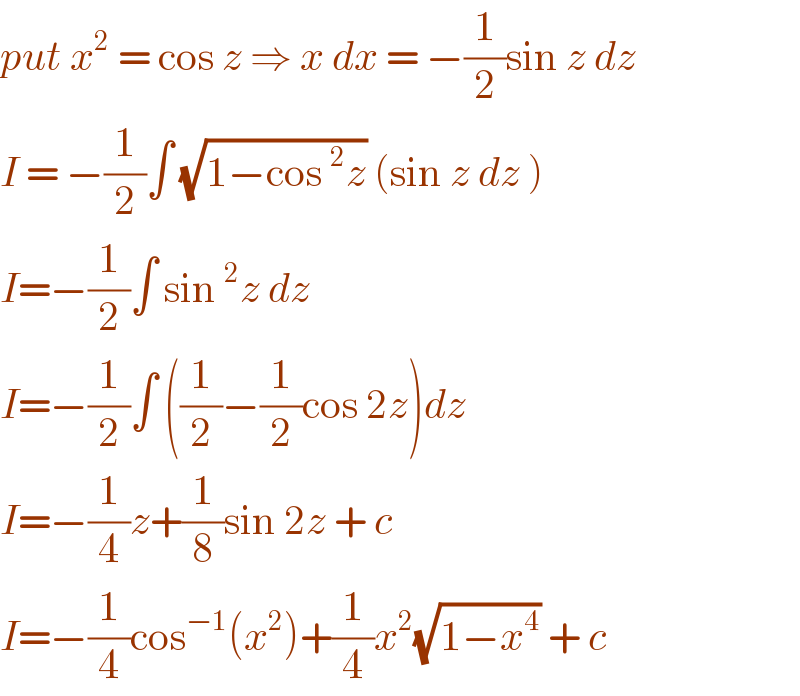
put x^2 = cos z ⇒ x dx = −(1/2)sin z dz I = −(1/2)∫ (√(1−cos^2 z)) (sin z dz ) I=−(1/2)∫ sin^2 z dz I=−(1/2)∫ ((1/2)−(1/2)cos 2z)dz I=−(1/4)z+(1/8)sin 2z + c I=−(1/4)cos^(−1) (x^2 )+(1/4)x^2 (√(1−x^4 )) + c
$${put}\:{x}^{\mathrm{2}} \:=\:\mathrm{cos}\:{z}\:\Rightarrow\:{x}\:{dx}\:=\:−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sin}\:{z}\:{dz} \\ $$$${I}\:=\:−\frac{\mathrm{1}}{\mathrm{2}}\int\:\sqrt{\mathrm{1}−\mathrm{cos}\:^{\mathrm{2}} {z}}\:\left(\mathrm{sin}\:{z}\:{dz}\:\right) \\ $$$${I}=−\frac{\mathrm{1}}{\mathrm{2}}\int\:\mathrm{sin}\:^{\mathrm{2}} {z}\:{dz}\: \\ $$$${I}=−\frac{\mathrm{1}}{\mathrm{2}}\int\:\left(\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{cos}\:\mathrm{2}{z}\right){dz} \\ $$$${I}=−\frac{\mathrm{1}}{\mathrm{4}}{z}+\frac{\mathrm{1}}{\mathrm{8}}\mathrm{sin}\:\mathrm{2}{z}\:+\:{c} \\ $$$${I}=−\frac{\mathrm{1}}{\mathrm{4}}\mathrm{cos}^{−\mathrm{1}} \left({x}^{\mathrm{2}} \right)+\frac{\mathrm{1}}{\mathrm{4}}{x}^{\mathrm{2}} \sqrt{\mathrm{1}−{x}^{\mathrm{4}} }\:+\:{c} \\ $$
Answered by ajfour last updated on 10/Dec/20
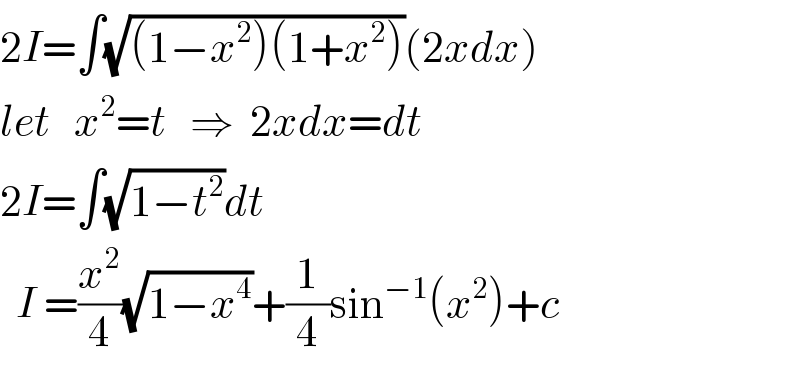
2I=∫(√((1−x^2 )(1+x^2 )))(2xdx) let x^2 =t ⇒ 2xdx=dt 2I=∫(√(1−t^2 ))dt I =(x^2 /4)(√(1−x^4 ))+(1/4)sin^(−1) (x^2 )+c
$$\mathrm{2}{I}=\int\sqrt{\left(\mathrm{1}−{x}^{\mathrm{2}} \right)\left(\mathrm{1}+{x}^{\mathrm{2}} \right)}\left(\mathrm{2}{xdx}\right) \\ $$$${let}\:\:\:{x}^{\mathrm{2}} ={t}\:\:\:\Rightarrow\:\:\mathrm{2}{xdx}={dt} \\ $$$$\mathrm{2}{I}=\int\sqrt{\mathrm{1}−{t}^{\mathrm{2}} }{dt} \\ $$$$\:\:{I}\:=\frac{{x}^{\mathrm{2}} }{\mathrm{4}}\sqrt{\mathrm{1}−{x}^{\mathrm{4}} }+\frac{\mathrm{1}}{\mathrm{4}}\mathrm{sin}^{−\mathrm{1}} \left({x}^{\mathrm{2}} \right)+{c} \\ $$
Answered by mathmax by abdo last updated on 10/Dec/20
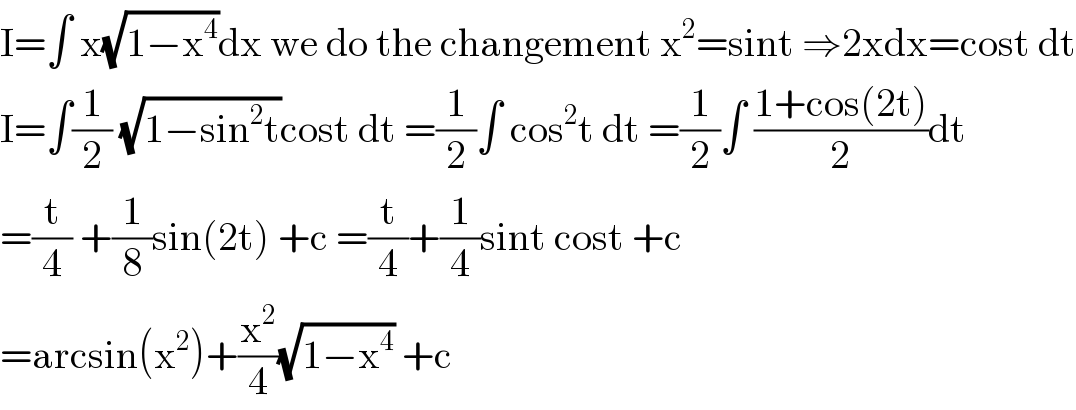
I=∫ x(√(1−x^4 ))dx we do the changement x^2 =sint ⇒2xdx=cost dt I=∫(1/2) (√(1−sin^2 t))cost dt =(1/2)∫ cos^2 t dt =(1/2)∫ ((1+cos(2t))/2)dt =(t/4) +(1/8)sin(2t) +c =(t/4)+(1/4)sint cost +c =arcsin(x^2 )+(x^2 /4)(√(1−x^4 )) +c
$$\mathrm{I}=\int\:\mathrm{x}\sqrt{\mathrm{1}−\mathrm{x}^{\mathrm{4}} }\mathrm{dx}\:\mathrm{we}\:\mathrm{do}\:\mathrm{the}\:\mathrm{changement}\:\mathrm{x}^{\mathrm{2}} =\mathrm{sint}\:\Rightarrow\mathrm{2xdx}=\mathrm{cost}\:\mathrm{dt} \\ $$$$\mathrm{I}=\int\frac{\mathrm{1}}{\mathrm{2}}\:\sqrt{\mathrm{1}−\mathrm{sin}^{\mathrm{2}} \mathrm{t}}\mathrm{cost}\:\mathrm{dt}\:=\frac{\mathrm{1}}{\mathrm{2}}\int\:\mathrm{cos}^{\mathrm{2}} \mathrm{t}\:\mathrm{dt}\:=\frac{\mathrm{1}}{\mathrm{2}}\int\:\frac{\mathrm{1}+\mathrm{cos}\left(\mathrm{2t}\right)}{\mathrm{2}}\mathrm{dt} \\ $$$$=\frac{\mathrm{t}}{\mathrm{4}}\:+\frac{\mathrm{1}}{\mathrm{8}}\mathrm{sin}\left(\mathrm{2t}\right)\:+\mathrm{c}\:=\frac{\mathrm{t}}{\mathrm{4}}+\frac{\mathrm{1}}{\mathrm{4}}\mathrm{sint}\:\mathrm{cost}\:+\mathrm{c} \\ $$$$=\mathrm{arcsin}\left(\mathrm{x}^{\mathrm{2}} \right)+\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{4}}\sqrt{\mathrm{1}−\mathrm{x}^{\mathrm{4}} }\:+\mathrm{c} \\ $$
Commented by mathmax by abdo last updated on 10/Dec/20
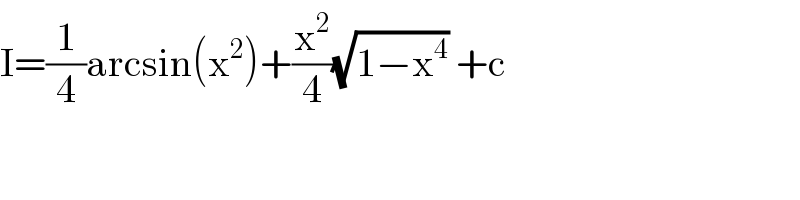
I=(1/4)arcsin(x^2 )+(x^2 /4)(√(1−x^4 )) +c
$$\mathrm{I}=\frac{\mathrm{1}}{\mathrm{4}}\mathrm{arcsin}\left(\mathrm{x}^{\mathrm{2}} \right)+\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{4}}\sqrt{\mathrm{1}−\mathrm{x}^{\mathrm{4}} }\:+\mathrm{c} \\ $$
Answered by Ar Brandon last updated on 10/Dec/20
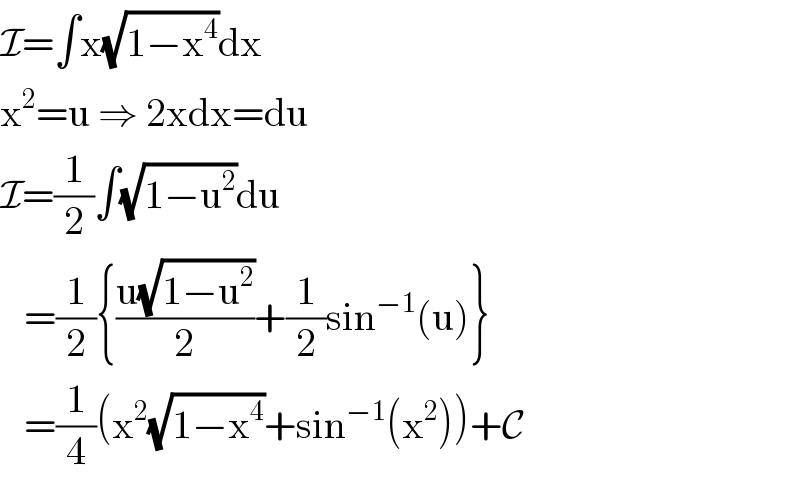
I=∫x(√(1−x^4 ))dx x^2 =u ⇒ 2xdx=du I=(1/2)∫(√(1−u^2 ))du =(1/2){((u(√(1−u^2 )))/2)+(1/2)sin^(−1) (u)} =(1/4)(x^2 (√(1−x^4 ))+sin^(−1) (x^2 ))+C
$$\mathcal{I}=\int\mathrm{x}\sqrt{\mathrm{1}−\mathrm{x}^{\mathrm{4}} }\mathrm{dx} \\ $$$$\mathrm{x}^{\mathrm{2}} =\mathrm{u}\:\Rightarrow\:\mathrm{2xdx}=\mathrm{du} \\ $$$$\mathcal{I}=\frac{\mathrm{1}}{\mathrm{2}}\int\sqrt{\mathrm{1}−\mathrm{u}^{\mathrm{2}} }\mathrm{du} \\ $$$$\:\:\:=\frac{\mathrm{1}}{\mathrm{2}}\left\{\frac{\mathrm{u}\sqrt{\mathrm{1}−\mathrm{u}^{\mathrm{2}} }}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sin}^{−\mathrm{1}} \left(\mathrm{u}\right)\right\} \\ $$$$\:\:\:=\frac{\mathrm{1}}{\mathrm{4}}\left(\mathrm{x}^{\mathrm{2}} \sqrt{\mathrm{1}−\mathrm{x}^{\mathrm{4}} }+\mathrm{sin}^{−\mathrm{1}} \left(\mathrm{x}^{\mathrm{2}} \right)\right)+\mathcal{C} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *