x-1-x-5-dx-

Question Number 113760 by gloriousman last updated on 15/Sep/20

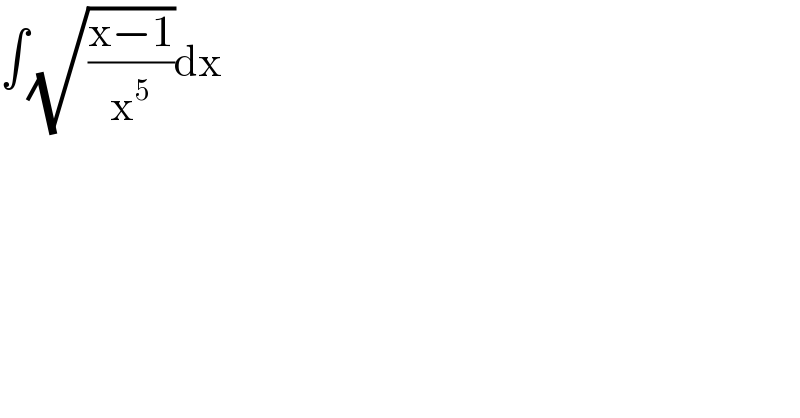
\int \sqrt{\frac{x - 1}{x^{5}}} dx

Answered by bemath last updated on 15/Sep/20

I = \int \frac{1}{x^{2}} \sqrt{\frac{x - 1}{x}} d x

I = \int \frac{1}{x^{2}} \sqrt{1 - \frac{1}{x}} d x

[l e t u = 1 - \frac{1}{x} \Rightarrow d u = \frac{d x}{x^{2}}]

I = \int u^{\frac{1}{2}} d u = \frac{2}{3} u^{\frac{3}{2}} + c

I = \frac{2}{3} (\frac{x - 1}{x}) \sqrt{\frac{x - 1}{x}} + c

Commented by gloriousman last updated on 15/Sep/20

Thanks