Question Number 111558 by Study last updated on 04/Sep/20

$$\int\sqrt[{{x}}]{{x}}{dx}=? \\ $$
Commented by Her_Majesty last updated on 04/Sep/20
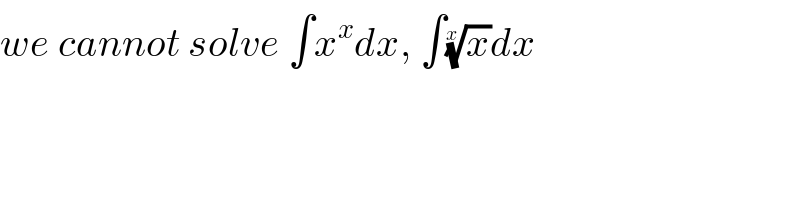
$${we}\:{cannot}\:{solve}\:\int{x}^{{x}} {dx},\:\int\sqrt[{{x}}]{{x}}{dx} \\ $$
Commented by bemath last updated on 04/Sep/20

$${waw}…{this}\:{very}\:{hard} \\ $$
Commented by mathdave last updated on 04/Sep/20
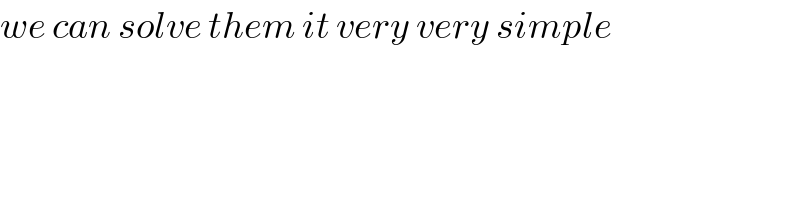
$${we}\:{can}\:{solve}\:{them}\:{it}\:{very}\:{very}\:{simple} \\ $$
Commented by Her_Majesty last updated on 04/Sep/20

$${show}\:{us} \\ $$
Commented by mathdave last updated on 04/Sep/20
![let me start by solving ∫x^x dx before coming to solve ∫(x)^(1/x) dx solution to ∫x^x dx let I=∫x^x dx=∫e^(xlnx) dx but the series term of e^x =Σ_(n=0) ^∞ (x^n /(n!)) and that of e^(xlnx) =Σ_(n=0) ^∞ (((xlnx)^n )/(n!)) I=Σ_(n=0) ^∞ (1/(n!))∫(xlnx)^n dx let y=−lnx,x=e^(−y) and dx=−e^(−y) dy now we have I=Σ_(n=0) ^∞ (1/(n!))∫(e^(−y) )^n (−y)^n (−e^(−y) )dy I=−Σ_(n=0) ^∞ (1/(n!))∫e^(−ny) e^(−y) (−1)^n (y)^n dy I=−Σ_(n=0) ^∞ (((−1)^n )/(n!))∫y^n e^(−y(n+1)) dy let z=y(n+1),y=(z/(n+1)) and dy=(dz/(n+1)) I=−Σ_(n=0) ^∞ (((−1)^n )/(n!))∫((z/(n+1)))^n e^(−z) ×(dz/(n+1)) I=−Σ_(n=0) ^∞ (((−1)^n )/(n!))∫((z^n e^(−z) )/((1+n)^n (1+n)))dz I=−Σ_(n=0) ^∞ (((−1)^n )/(n!(1+n)^(n+1) ))∫z^n e^(−z) dz from gamma function Γ(l,x)=∫x^(l−1) e^(−x) d when compare this to the original function we have l−1=n then l=(n+1) and z=x so Γ(n+1,z)=∫z^n e^(−z) dx but z=y(n+1) and y=−lnx finally z=−(k+1)lnx if pluggin these we have I=−Σ_(n=0) ^∞ (((−1)^n )/(n!(n+1)^(n+1) ))×−Γ[n+1,(n+1)lnx] ∵∫x^x dx=Σ_(n=0) ^∞ (((−1)^n )/(n!(n+1)^(n+1) ))Γ[n+1,(n+1)lnx] by mathdave(04/09/2020)](https://www.tinkutara.com/question/Q111589.png)
$${let}\:{me}\:{start}\:{by}\:{solving}\:\int{x}^{{x}} {dx}\:{before} \\ $$$${coming}\:{to}\:{solve}\:\int\sqrt[{{x}}]{{x}}{dx} \\ $$$${solution}\:{to}\:\int{x}^{{x}} {dx} \\ $$$${let}\:{I}=\int{x}^{{x}} {dx}=\int{e}^{{x}\mathrm{ln}{x}} {dx} \\ $$$${but}\:{the}\:{series}\:{term}\:{of} \\ $$$${e}^{{x}} =\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{{x}^{{n}} }{{n}!}\:\:{and}\:{that}\:{of}\: \\ $$$${e}^{{x}\mathrm{ln}{x}} =\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left({x}\mathrm{ln}{x}\right)^{{n}} }{{n}!} \\ $$$${I}=\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}!}\int\left({x}\mathrm{ln}{x}\right)^{{n}} {dx} \\ $$$${let}\:{y}=−\mathrm{ln}{x},{x}={e}^{−{y}} \:\:\:{and}\:\:{dx}=−{e}^{−{y}} {dy} \\ $$$${now}\:{we}\:{have} \\ $$$${I}=\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}!}\int\left({e}^{−{y}} \right)^{{n}} \left(−{y}\right)^{{n}} \left(−{e}^{−{y}} \right){dy} \\ $$$${I}=−\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}!}\int{e}^{−{ny}} {e}^{−{y}} \left(−\mathrm{1}\right)^{{n}} \left({y}\right)^{{n}} {dy} \\ $$$${I}=−\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}} }{{n}!}\int{y}^{{n}} {e}^{−{y}\left({n}+\mathrm{1}\right)} {dy} \\ $$$${let}\:{z}={y}\left({n}+\mathrm{1}\right),{y}=\frac{{z}}{{n}+\mathrm{1}}\:\:{and}\:{dy}=\frac{{dz}}{{n}+\mathrm{1}} \\ $$$${I}=−\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}} }{{n}!}\int\left(\frac{{z}}{{n}+\mathrm{1}}\right)^{{n}} {e}^{−{z}} ×\frac{{dz}}{{n}+\mathrm{1}} \\ $$$${I}=−\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}} }{{n}!}\int\frac{{z}^{{n}} {e}^{−{z}} }{\left(\mathrm{1}+{n}\right)^{{n}} \left(\mathrm{1}+{n}\right)}{dz} \\ $$$${I}=−\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}} }{{n}!\left(\mathrm{1}+{n}\right)^{{n}+\mathrm{1}} }\int{z}^{{n}} {e}^{−{z}} {dz} \\ $$$${from}\:{gamma}\:{function} \\ $$$$\Gamma\left({l},{x}\right)=\int{x}^{{l}−\mathrm{1}} {e}^{−{x}} {d} \\ $$$${when}\:{compare}\:{this}\:{to}\:{the}\:{original} \\ $$$${function}\:{we}\:{have}\: \\ $$$${l}−\mathrm{1}={n}\:\:{then}\:{l}=\left({n}+\mathrm{1}\right)\:{and}\:{z}={x}\:{so}\: \\ $$$$\Gamma\left({n}+\mathrm{1},{z}\right)=\int{z}^{{n}} {e}^{−{z}} {dx} \\ $$$${but}\:{z}={y}\left({n}+\mathrm{1}\right)\:\:{and}\:{y}=−\mathrm{ln}{x}\:\:{finally} \\ $$$${z}=−\left({k}+\mathrm{1}\right)\mathrm{ln}{x} \\ $$$${if}\:{pluggin}\:\:{these}\:\:{we}\:{have}\: \\ $$$${I}=−\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}} }{{n}!\left({n}+\mathrm{1}\right)^{{n}+\mathrm{1}} }×−\Gamma\left[{n}+\mathrm{1},\left({n}+\mathrm{1}\right)\mathrm{ln}{x}\right] \\ $$$$\because\int{x}^{{x}} {dx}=\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}} }{{n}!\left({n}+\mathrm{1}\right)^{{n}+\mathrm{1}} }\Gamma\left[{n}+\mathrm{1},\left({n}+\mathrm{1}\right)\mathrm{ln}{x}\right] \\ $$$${by}\:{mathdave}\left(\mathrm{04}/\mathrm{09}/\mathrm{2020}\right) \\ $$
Commented by Her_Majesty last updated on 04/Sep/20
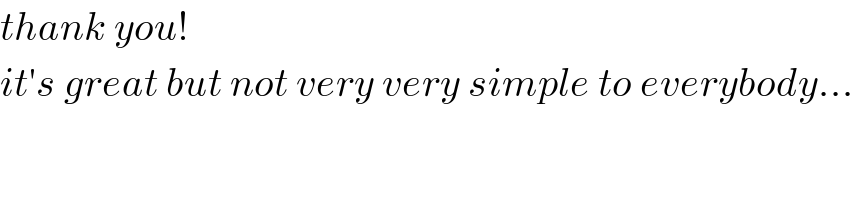
$${thank}\:{you}! \\ $$$${it}'{s}\:{great}\:{but}\:{not}\:{very}\:{very}\:{simple}\:{to}\:{everybody}… \\ $$
Commented by mathdave last updated on 04/Sep/20
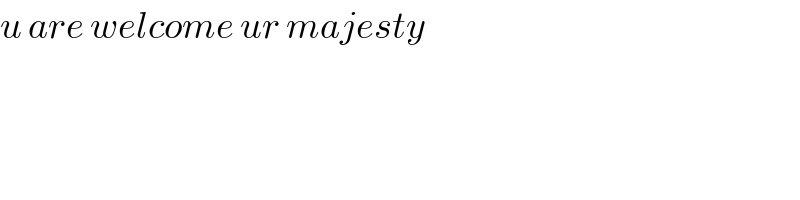
$${u}\:{are}\:{welcome}\:{ur}\:{majesty} \\ $$
Commented by bemath last updated on 04/Sep/20
$${waw}..{amazing}…{this}\:{is}\:{super}\:{very}\:{simple} \\ $$
Commented by Tawa11 last updated on 06/Sep/21

$$\mathrm{great}\:\mathrm{sir} \\ $$
Answered by mathdave last updated on 04/Sep/20
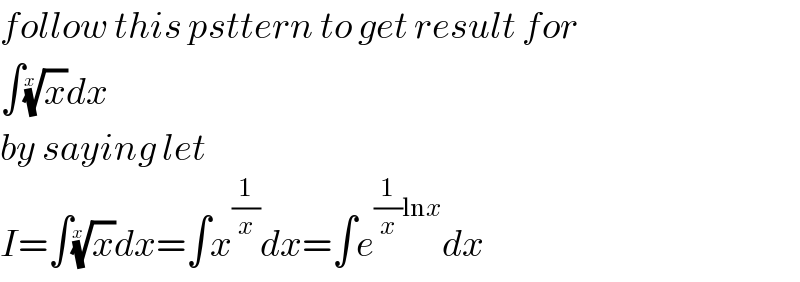
$${follow}\:{this}\:{psttern}\:{to}\:{get}\:{result}\:{for}\: \\ $$$$\int\sqrt[{{x}}]{{x}}{dx} \\ $$$${by}\:{saying}\:{let}\: \\ $$$${I}=\int\sqrt[{{x}}]{{x}}{dx}=\int{x}^{\frac{\mathrm{1}}{{x}}} {dx}=\int{e}^{\frac{\mathrm{1}}{{x}}\mathrm{ln}{x}} {dx} \\ $$
