Question Number 176554 by mnjuly1970 last updated on 21/Sep/22
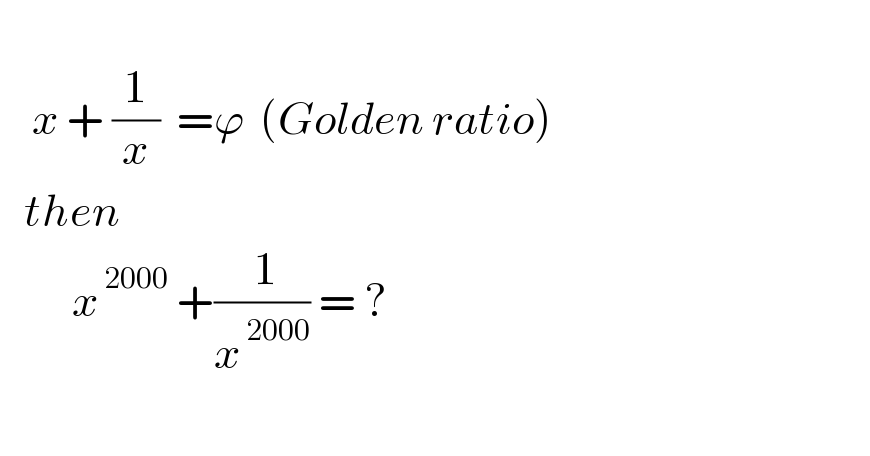
$$ \\ $$$$\:\:\:\:{x}\:+\:\frac{\mathrm{1}}{{x}}\:\:=\varphi\:\:\left({Golden}\:{ratio}\right) \\ $$$$\:\:\:{then} \\ $$$$\:\:\:\:\:\:\:\:\:{x}^{\:\mathrm{2000}} \:+\frac{\:\mathrm{1}}{{x}^{\:\mathrm{2000}} }\:=\:? \\ $$$$ \\ $$
Answered by Peace last updated on 21/Sep/22
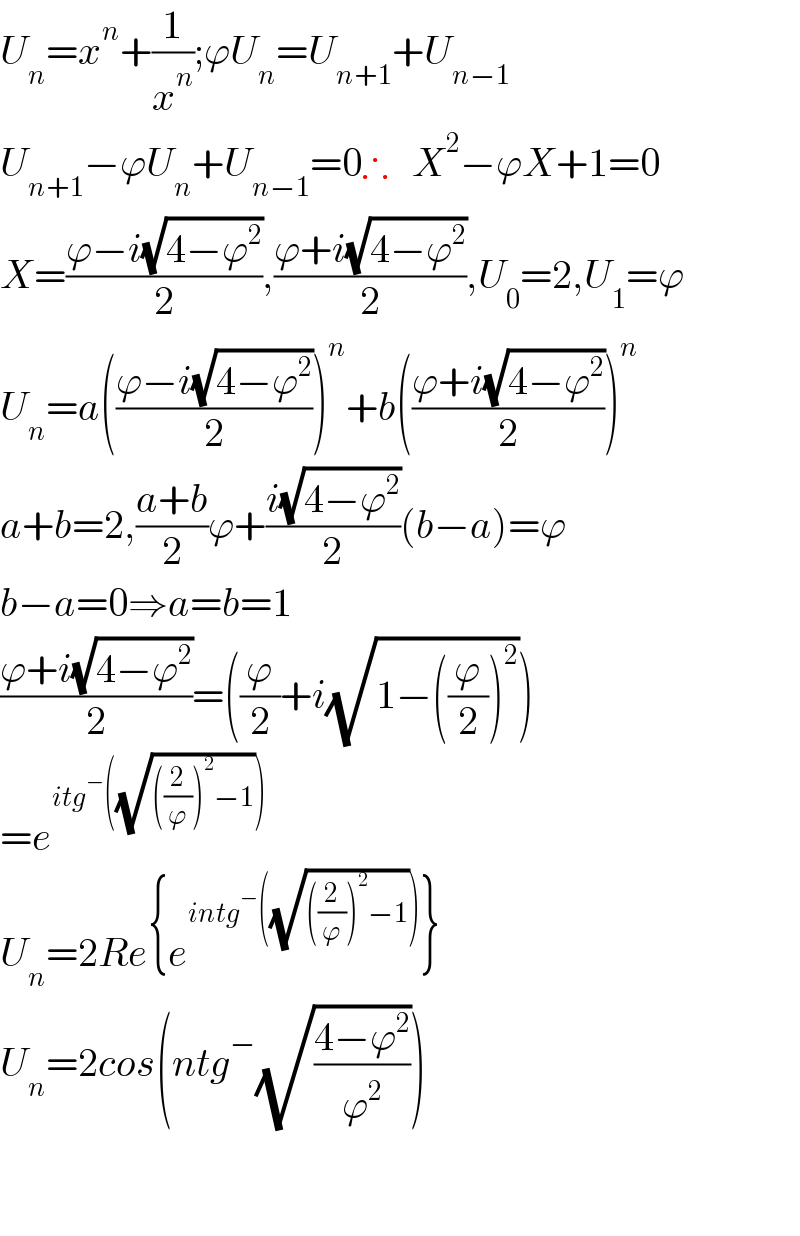
$${U}_{{n}} ={x}^{{n}} +\frac{\mathrm{1}}{{x}^{{n}} };\varphi{U}_{{n}} ={U}_{{n}+\mathrm{1}} +{U}_{{n}−\mathrm{1}} \\ $$$${U}_{{n}+\mathrm{1}} −\varphi{U}_{{n}} +{U}_{{n}−\mathrm{1}} =\mathrm{0}\therefore\:\:\:{X}^{\mathrm{2}} −\varphi{X}+\mathrm{1}=\mathrm{0} \\ $$$${X}=\frac{\varphi−{i}\sqrt{\mathrm{4}−\varphi^{\mathrm{2}} }}{\mathrm{2}},\frac{\varphi+{i}\sqrt{\mathrm{4}−\varphi^{\mathrm{2}} }}{\mathrm{2}},{U}_{\mathrm{0}} =\mathrm{2},{U}_{\mathrm{1}} =\varphi \\ $$$${U}_{{n}} ={a}\left(\frac{\varphi−{i}\sqrt{\mathrm{4}−\varphi^{\mathrm{2}} }}{\mathrm{2}}\right)^{{n}} +{b}\left(\frac{\varphi+{i}\sqrt{\mathrm{4}−\varphi^{\mathrm{2}} }}{\mathrm{2}}\right)^{{n}} \\ $$$${a}+{b}=\mathrm{2},\frac{{a}+{b}}{\mathrm{2}}\varphi+\frac{{i}\sqrt{\mathrm{4}−\varphi^{\mathrm{2}} }}{\mathrm{2}}\left({b}−{a}\right)=\varphi \\ $$$${b}−{a}=\mathrm{0}\Rightarrow{a}={b}=\mathrm{1} \\ $$$$\frac{\varphi+{i}\sqrt{\mathrm{4}−\varphi^{\mathrm{2}} }}{\mathrm{2}}=\left(\frac{\varphi}{\mathrm{2}}+{i}\sqrt{\mathrm{1}−\left(\frac{\varphi}{\mathrm{2}}\right)^{\mathrm{2}} }\right) \\ $$$$={e}^{{itg}^{−} \left(\sqrt{\left(\frac{\mathrm{2}}{\varphi}\right)^{\mathrm{2}} −\mathrm{1}}\right)} \\ $$$${U}_{{n}} =\mathrm{2}{Re}\left\{{e}^{{intg}^{−} \left(\sqrt{\left(\frac{\mathrm{2}}{\varphi}\right)^{\mathrm{2}} −\mathrm{1}}\right)} \right\} \\ $$$${U}_{{n}} =\mathrm{2}{cos}\left({ntg}^{−} \sqrt{\frac{\mathrm{4}−\varphi^{\mathrm{2}} }{\varphi^{\mathrm{2}} }}\right) \\ $$$$ \\ $$$$ \\ $$
Commented by Tawa11 last updated on 23/Sep/22

$$\mathrm{Great}\:\mathrm{sir} \\ $$
Commented by Peace last updated on 25/Sep/22

$${Withe}\:{pleasur} \\ $$
Answered by Frix last updated on 22/Sep/22
![x+(1/x)=ϕ x^2 −ϕx+1=0 [x^5 −1=0 (x+1)(x^4 −x^3 +x^2 −x+1)=0 (x+1)(x^2 −((1−(√5))/2)x+1)(x^2 −((1+(√5))/2)+1)=0] ⇒ x=cos (π/5) ±i sin (π/5) =e^(±i(π/5)) (e^(±i(π/5)) )^(2000) =e^(±400iπ) =e^(±iπ) =1 ⇒ x^(2000) +(1/x^(2000) )=e^(±iπ) +e^(∓iπ) =1+1=2](https://www.tinkutara.com/question/Q176591.png)
$${x}+\frac{\mathrm{1}}{{x}}=\varphi \\ $$$${x}^{\mathrm{2}} −\varphi{x}+\mathrm{1}=\mathrm{0} \\ $$$$\left[{x}^{\mathrm{5}} −\mathrm{1}=\mathrm{0}\right. \\ $$$$\:\:\:\:\:\left({x}+\mathrm{1}\right)\left({x}^{\mathrm{4}} −{x}^{\mathrm{3}} +{x}^{\mathrm{2}} −{x}+\mathrm{1}\right)=\mathrm{0} \\ $$$$\left.\:\:\:\:\:\left({x}+\mathrm{1}\right)\left({x}^{\mathrm{2}} −\frac{\mathrm{1}−\sqrt{\mathrm{5}}}{\mathrm{2}}{x}+\mathrm{1}\right)\left({x}^{\mathrm{2}} −\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}+\mathrm{1}\right)=\mathrm{0}\right] \\ $$$$\Rightarrow \\ $$$${x}=\mathrm{cos}\:\frac{\pi}{\mathrm{5}}\:\pm\mathrm{i}\:\mathrm{sin}\:\frac{\pi}{\mathrm{5}}\:=\mathrm{e}^{\pm\mathrm{i}\frac{\pi}{\mathrm{5}}} \\ $$$$\left(\mathrm{e}^{\pm\mathrm{i}\frac{\pi}{\mathrm{5}}} \right)^{\mathrm{2000}} =\mathrm{e}^{\pm\mathrm{400i}\pi} =\mathrm{e}^{\pm\mathrm{i}\pi} =\mathrm{1} \\ $$$$\Rightarrow\:{x}^{\mathrm{2000}} +\frac{\mathrm{1}}{{x}^{\mathrm{2000}} }=\mathrm{e}^{\pm\mathrm{i}\pi} +\mathrm{e}^{\mp\mathrm{i}\pi} =\mathrm{1}+\mathrm{1}=\mathrm{2} \\ $$
