Question Number 153339 by amin96 last updated on 06/Sep/21
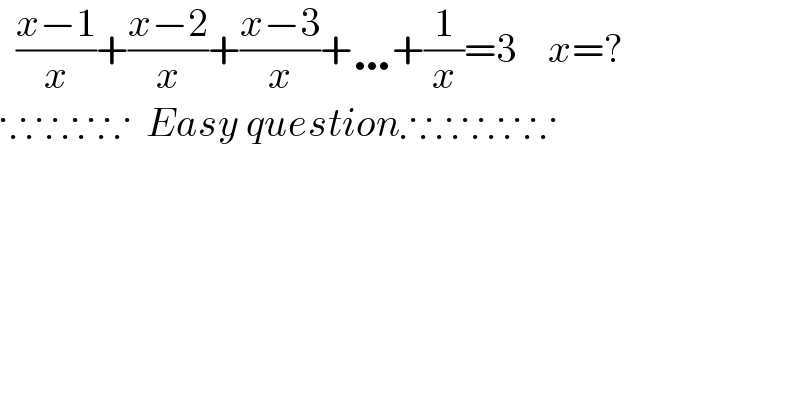
$$\:\:\frac{{x}−\mathrm{1}}{{x}}+\frac{{x}−\mathrm{2}}{{x}}+\frac{{x}−\mathrm{3}}{{x}}+\ldots+\frac{\mathrm{1}}{{x}}=\mathrm{3}\:\:\:\:{x}=? \\ $$$$\because\therefore\because\therefore\because\:\:{Easy}\:{question}\therefore\because\therefore\because\therefore\because \\ $$
Answered by MJS_new last updated on 06/Sep/21
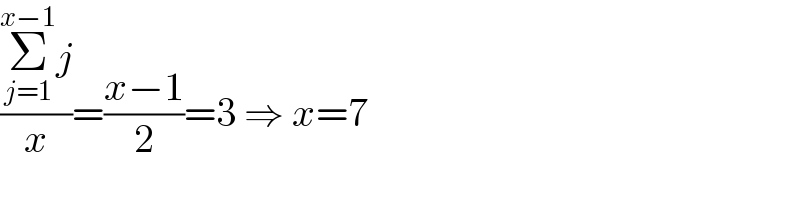
$$\frac{\underset{{j}=\mathrm{1}} {\overset{{x}−\mathrm{1}} {\sum}}{j}}{{x}}=\frac{{x}−\mathrm{1}}{\mathrm{2}}=\mathrm{3}\:\Rightarrow\:{x}=\mathrm{7} \\ $$
Answered by talminator2856791 last updated on 06/Sep/21
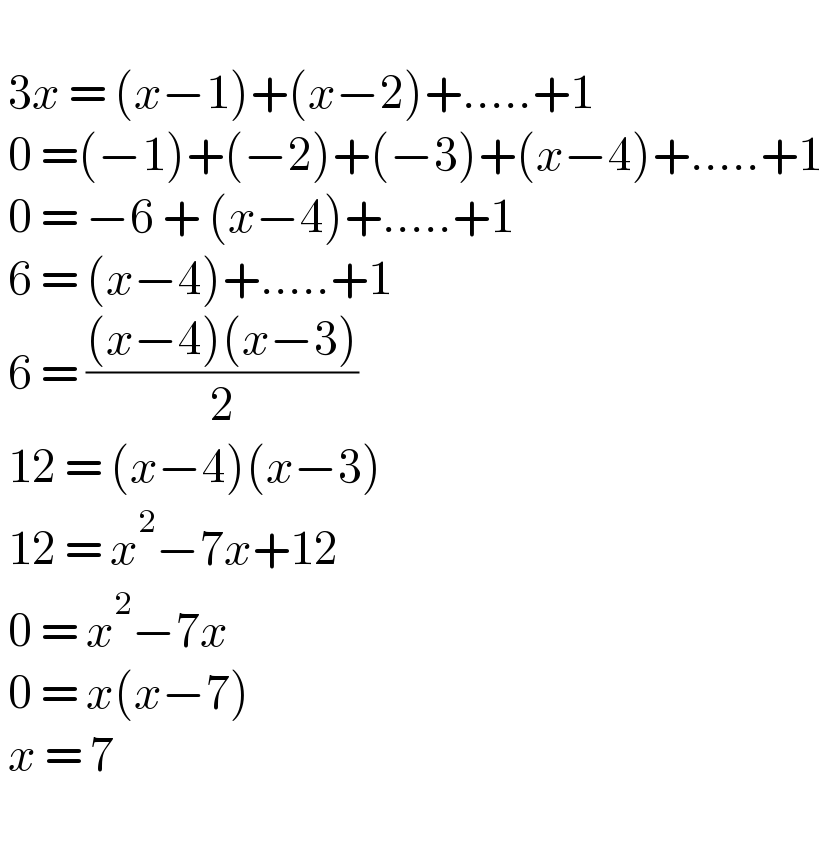
$$\: \\ $$$$\:\mathrm{3}{x}\:=\:\left({x}−\mathrm{1}\right)+\left({x}−\mathrm{2}\right)+…..+\mathrm{1} \\ $$$$\:\mathrm{0}\:=\left(−\mathrm{1}\right)+\left(−\mathrm{2}\right)+\left(−\mathrm{3}\right)+\left({x}−\mathrm{4}\right)+…..+\mathrm{1} \\ $$$$\:\mathrm{0}\:=\:−\mathrm{6}\:+\:\left({x}−\mathrm{4}\right)+…..+\mathrm{1} \\ $$$$\:\mathrm{6}\:=\:\left({x}−\mathrm{4}\right)+…..+\mathrm{1} \\ $$$$\:\mathrm{6}\:=\:\frac{\left({x}−\mathrm{4}\right)\left({x}−\mathrm{3}\right)}{\mathrm{2}} \\ $$$$\:\mathrm{12}\:=\:\left({x}−\mathrm{4}\right)\left({x}−\mathrm{3}\right) \\ $$$$\:\mathrm{12}\:=\:{x}^{\mathrm{2}} −\mathrm{7}{x}+\mathrm{12} \\ $$$$\:\mathrm{0}\:=\:{x}^{\mathrm{2}} −\mathrm{7}{x} \\ $$$$\:\mathrm{0}\:=\:{x}\left({x}−\mathrm{7}\right) \\ $$$$\:{x}\:=\:\mathrm{7} \\ $$$$\: \\ $$
