Question Number 169533 by cortano1 last updated on 02/May/22
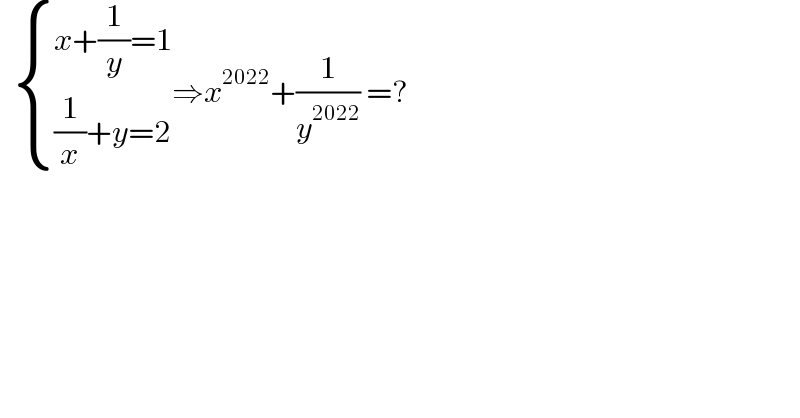
$$\:\:\begin{cases}{{x}+\frac{\mathrm{1}}{{y}}=\mathrm{1}}\\{\frac{\mathrm{1}}{{x}}+{y}=\mathrm{2}}\end{cases}\Rightarrow{x}^{\mathrm{2022}} +\frac{\mathrm{1}}{{y}^{\mathrm{2022}} }\:=? \\ $$
Commented by greougoury555 last updated on 02/May/22

$$\:\:{x}=\frac{{y}−\mathrm{1}}{{y}}\:\wedge\:\frac{{y}}{{y}−\mathrm{1}}+{y}\:=\:\mathrm{2} \\ $$$$\Rightarrow{y}+{y}^{\mathrm{2}} −{y}\:=\:\mathrm{2}{y}−\mathrm{2} \\ $$$$\Rightarrow{y}^{\mathrm{2}} −\mathrm{2}{y}+\mathrm{2}\:=\mathrm{0} \\ $$$$\Rightarrow\left({y}−\mathrm{1}\right)^{\mathrm{2}} +\mathrm{1}=\mathrm{0} \\ $$$$\Rightarrow{y}=\mathrm{1}+{i}\:;\:{x}=\frac{{i}}{\mathrm{1}+{i}}\:.\frac{\mathrm{1}−{i}}{\mathrm{1}−{i}}\:=\frac{\mathrm{1}+{i}}{\mathrm{2}}=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}{e}^{{i}\frac{\pi}{\mathrm{4}}} \\ $$$$\Rightarrow\frac{\mathrm{1}}{{y}}\:=\:\frac{\mathrm{1}}{\mathrm{1}+{i}}\:.\frac{\mathrm{1}−{i}}{\mathrm{1}−{i}}\:=\:\frac{\mathrm{1}−{i}}{\mathrm{2}}=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}{e}^{−{i}\frac{\pi}{\mathrm{4}}} \\ $$$$\Rightarrow{x}^{\mathrm{2022}} +\frac{\mathrm{1}}{{y}^{\mathrm{2022}} }\:=\mathrm{2}^{−\mathrm{1011}} {e}^{{i}\left(\frac{\mathrm{1011}\pi}{\mathrm{2}}\right)} +\mathrm{2}^{−\mathrm{1011}} {e}^{−{i}\left(\frac{\mathrm{1011}\pi}{\mathrm{2}}\right)} \\ $$$$\:=\mathrm{2}^{−\mathrm{1011}} \:\left(\mathrm{cos}\:\frac{\mathrm{1011}\pi}{\mathrm{2}}\right) \\ $$$$=\:\mathrm{2}^{−\mathrm{1011}} ×\mathrm{0}\:=\:\mathrm{0}\: \\ $$
