Question Number 111008 by Khanacademy last updated on 01/Sep/20
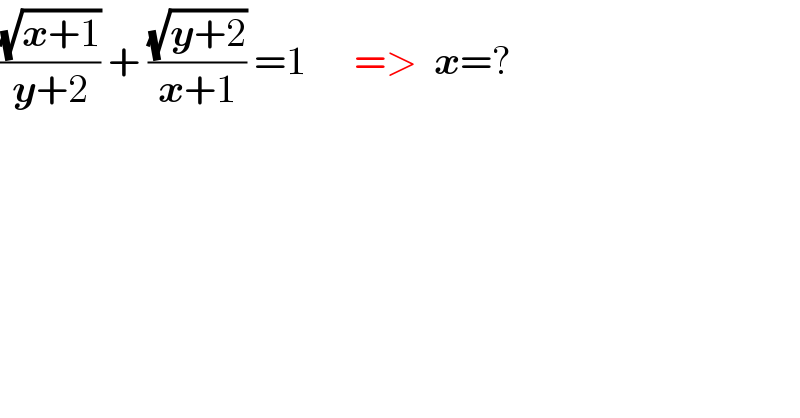
$$\frac{\sqrt{\boldsymbol{{x}}+\mathrm{1}}}{\boldsymbol{{y}}+\mathrm{2}}\:+\:\frac{\sqrt{\boldsymbol{{y}}+\mathrm{2}}}{\boldsymbol{{x}}+\mathrm{1}}\:=\mathrm{1}\:\:\:\:\:\:=>\:\:\boldsymbol{{x}}=? \\ $$
Commented by Rasheed.Sindhi last updated on 01/Sep/20

$${x}\:{in}\:{terms}\:{of}\:{y}? \\ $$
Commented by Khanacademy last updated on 01/Sep/20

$$??????? \\ $$
Commented by Her_Majesty last updated on 01/Sep/20

$${complicated}… \\ $$$$\frac{{a}}{{b}^{\mathrm{2}} }+\frac{{b}}{{a}^{\mathrm{2}} }=\mathrm{1} \\ $$$${a}^{\mathrm{3}} −{a}^{\mathrm{2}} {b}^{\mathrm{2}} +{b}^{\mathrm{3}} =\mathrm{0} \\ $$$${a}={t}+\frac{{b}^{\mathrm{2}} }{\mathrm{3}} \\ $$$${t}^{\mathrm{3}} −\frac{{b}^{\mathrm{4}} }{\mathrm{3}}{t}−\frac{{b}^{\mathrm{3}} \left(\mathrm{2}{b}^{\mathrm{3}} −\mathrm{27}\right)}{\mathrm{27}}=\mathrm{0} \\ $$$${we}\:{can}\:{solve}\:{this}\:{for}\:{t} \\ $$$${D}=\frac{{b}^{\mathrm{6}} }{\mathrm{4}}−\frac{{b}^{\mathrm{9}} }{\mathrm{27}} \\ $$$${we}\:{need}\:{Cardano}'{s}\:{or}\:{the}\:{Trigonometric} \\ $$$${solution} \\ $$$${depending}\:{on}\:{the}\:{desired}\:{domain}: \\ $$$$\mathbb{R}:\:{x}>−\mathrm{1}\wedge{y}>−\mathrm{2}\:\Rightarrow\:{a}>\mathrm{0}\wedge{b}>\mathrm{0} \\ $$$$\mathbb{C}:\:{x}\neq−\mathrm{1}\wedge{y}\neq−\mathrm{2}\:\Rightarrow\:{a}\neq\mathrm{0}\wedge{b}\neq\mathrm{0} \\ $$
