Question Number 86741 by M±th+et£s last updated on 30/Mar/20

$$\begin{cases}{{x}+\mathrm{10}{y}+\mathrm{50}{z}=\mathrm{500}}\\{{x}+{y}+{z}=\mathrm{100}}\end{cases} \\ $$$$ \\ $$$${find}\:{x},{y},{z} \\ $$
Commented by mr W last updated on 30/Mar/20

$${x},{y},{z}\in{N}\:? \\ $$
Commented by M±th+et£s last updated on 30/Mar/20

$${yes}\:{sir} \\ $$
Commented by mr W last updated on 30/Mar/20
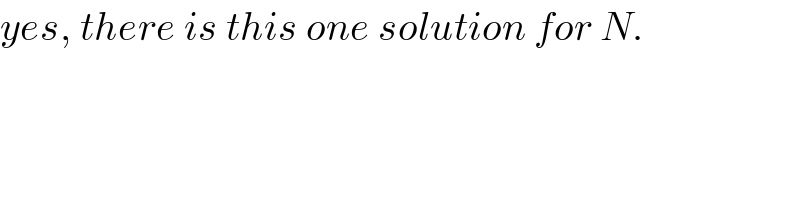
$${yes},\:{there}\:{is}\:{this}\:{one}\:{solution}\:{for}\:{N}. \\ $$
Commented by M±th+et£s last updated on 30/Mar/20

$${x}=\mathrm{60} \\ $$$${y}=\mathrm{39} \\ $$$${z}=\mathrm{1} \\ $$
Answered by mr W last updated on 30/Mar/20

$${x}+\mathrm{10}{y}+\mathrm{50}{z}=\mathrm{500} \\ $$$${x}=\mathrm{10}{x}' \\ $$$$\mathrm{10}{x}'+\mathrm{10}{y}+\mathrm{50}{z}=\mathrm{500} \\ $$$$\Rightarrow{x}'+{y}+\mathrm{5}{z}=\mathrm{50} \\ $$$${x}'+{y}=\mathrm{1} \\ $$$$\Rightarrow{x}'=−{k} \\ $$$$\Rightarrow{y}={k}+\mathrm{1} \\ $$$${u}+\mathrm{5}{z}=\mathrm{50} \\ $$$$\Rightarrow{u}=−\mathrm{5}{h} \\ $$$$\Rightarrow{z}={h}+\mathrm{10} \\ $$$${x}'=\left(−\mathrm{5}{h}\right)\left(−{k}\right)=\mathrm{5}{hk}={n}\:\Rightarrow{x}=\mathrm{10}{n} \\ $$$${y}=\left(−\mathrm{5}{h}\right)\left({k}+\mathrm{1}\right)=−{n}−\mathrm{5}{h} \\ $$$$ \\ $$$$\mathrm{10}{n}−{n}−\mathrm{5}{h}+{h}+\mathrm{10}=\mathrm{100} \\ $$$$\mathrm{9}{n}−\mathrm{4}{h}=\mathrm{90} \\ $$$$\Rightarrow{n}=\mathrm{4}{k}+\mathrm{6} \\ $$$$\Rightarrow{h}=\mathrm{9}{k}−\mathrm{9} \\ $$$$ \\ $$$${general}\:{solution}: \\ $$$$\Rightarrow{x}=\mathrm{20}\left(\mathrm{2}{k}+\mathrm{3}\right) \\ $$$$\Rightarrow{y}=\mathrm{39}−\mathrm{49}{k} \\ $$$$\Rightarrow{z}=\mathrm{9}{k}+\mathrm{1} \\ $$$${for}\:{x},{y},{z}\in{N} \\ $$$${k}=\mathrm{0}: \\ $$$${x}=\mathrm{60},\:{y}=\mathrm{39},\:{z}=\mathrm{1} \\ $$
Commented by M±th+et£s last updated on 30/Mar/20

$${thank}\:{you}\:{sir}\: \\ $$
Commented by liki last updated on 31/Mar/20
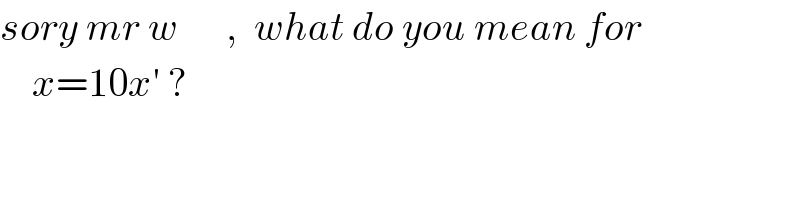
$${sory}\:{mr}\:{w}\:\:\:\:\:\:,\:\:{what}\:{do}\:{you}\:{mean}\:{for}\: \\ $$$$\:\:\:\:{x}=\mathrm{10}{x}'\:? \\ $$
Commented by mr W last updated on 31/Mar/20
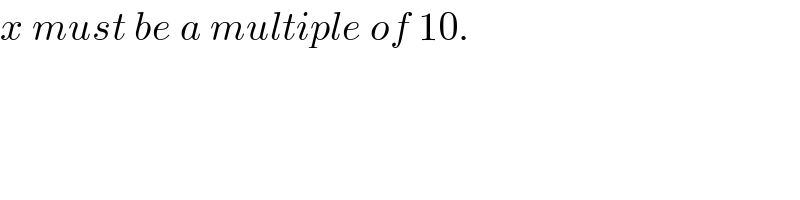
$${x}\:{must}\:{be}\:{a}\:{multiple}\:{of}\:\mathrm{10}. \\ $$
