Menu Close

x-11-x-x-7-x-5-205-16-solve-for-x-undecic-equation-

Tinku Tara 0 Comments
Pin




Question Number 175972 by Linton last updated on 10/Sep/22
((x^(11) +x)/(x^7 +x^5 )) = ((205)/(16)) solve for x (undecic equation )
$$\frac{{x}^{\mathrm{11}} +{x}}{{x}^{\mathrm{7}} +{x}^{\mathrm{5}} }\:=\:\frac{\mathrm{205}}{\mathrm{16}} \\ $$$${solve}\:{for}\:{x}\:\left({undecic}\:{equation}\:\right) \\ $$
Answered by BaliramKumar last updated on 10/Sep/22
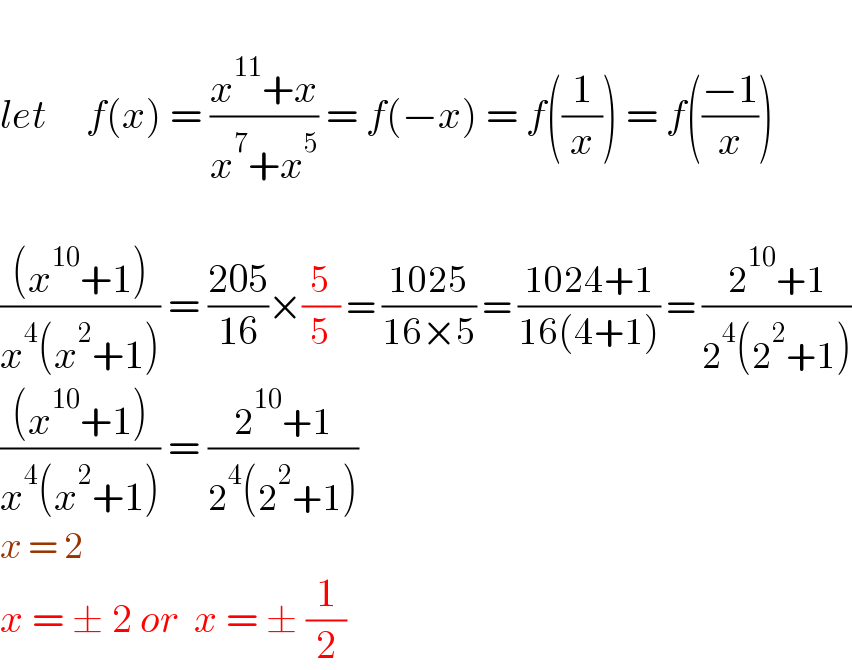
let f(x) = ((x^(11) +x)/(x^7 +x^5 )) = f(−x) = f((1/x)) = f(((−1)/x)) (((x^(10) +1))/(x^4 (x^2 +1))) = ((205)/(16))×(5/5) = ((1025)/(16×5)) = ((1024+1)/(16(4+1))) = ((2^(10) +1)/(2^4 (2^2 +1))) (((x^(10) +1))/(x^4 (x^2 +1))) = ((2^(10) +1)/(2^4 (2^2 +1))) x = 2 x = ± 2 or x = ± (1/2)
$$ \\ $$$${let}\:\:\:\:\:{f}\left({x}\right)\:=\:\frac{{x}^{\mathrm{11}} +{x}}{{x}^{\mathrm{7}} +{x}^{\mathrm{5}} }\:=\:{f}\left(−{x}\right)\:=\:{f}\left(\frac{\mathrm{1}}{{x}}\right)\:=\:{f}\left(\frac{−\mathrm{1}}{{x}}\right) \\ $$$$ \\ $$$$\frac{\left({x}^{\mathrm{10}} +\mathrm{1}\right)}{{x}^{\mathrm{4}} \left({x}^{\mathrm{2}} +\mathrm{1}\right)}\:=\:\frac{\mathrm{205}}{\mathrm{16}}×\frac{\mathrm{5}}{\mathrm{5}}\:=\:\frac{\mathrm{1025}}{\mathrm{16}×\mathrm{5}}\:=\:\frac{\mathrm{1024}+\mathrm{1}}{\mathrm{16}\left(\mathrm{4}+\mathrm{1}\right)}\:=\:\frac{\mathrm{2}^{\mathrm{10}} +\mathrm{1}}{\mathrm{2}^{\mathrm{4}} \left(\mathrm{2}^{\mathrm{2}} +\mathrm{1}\right)} \\ $$$$\frac{\left({x}^{\mathrm{10}} +\mathrm{1}\right)}{{x}^{\mathrm{4}} \left({x}^{\mathrm{2}} +\mathrm{1}\right)}\:=\:\frac{\mathrm{2}^{\mathrm{10}} +\mathrm{1}}{\mathrm{2}^{\mathrm{4}} \left(\mathrm{2}^{\mathrm{2}} +\mathrm{1}\right)} \\ $$$${x}\:=\:\mathrm{2} \\ $$$${x}\:=\:\pm\:\mathrm{2}\:{or}\:\:{x}\:=\:\pm\:\frac{\mathrm{1}}{\mathrm{2}} \\ $$
Answered by Rasheed.Sindhi last updated on 11/Sep/22
((x^(11) +x)/(x^7 +x^5 )) = ((205)/(16)) (( ((x^(11) +x)/x^6 ) )/((x^7 +x^5 )/x^6 ))=((205)/(16)) ((x^5 +(1/x^5 ))/(x+(1/x)))=((205)/(16)) x+(1/x)=u (x+(1/x))^3 =u^3 x^3 +(1/x^3 )+3(x+(1/x))=u^3 x^3 +(1/x^3 )=u^3 −3u..............(i) (x+(1/x))^2 =u^2 x^2 +(1/x^2 )=u^2 −2................(ii) (i)×(ii): x^5 +(1/x^5 )+x+(1/x)=u^5 −3u^3 −2u^3 +6u x^5 +(1/x^5 )=u^5 −5u^3 +5u ((u^5 −5u^3 +5u)/u)=((205)/(16)) u^4 −5u^2 +5−((205)/(16))=0 16u^4 −80u^2 −125=0 u^2 =((80±(√(6400+8000)))/(32))=((80±120)/(32))=((25)/4),−(5/4) u=±(5/2),±((i(√5))/2) x+(1/x)=±(5/2) ∣ x+(1/x)=±((i(√5))/2)^((A)) 2x^2 +2=±5x { ((2x^2 +2=5x⇒2x^2 −5x+2=0^• )),((2x^2 +2=−5x⇒2x^2 +5x+2=0^(••) )) :} ^• 2x^2 −5x+2=0 x=((5±(√(25−16)))/4) =((5±3)/4)=2,(1/2) ^(••) 2x^2 +5x+2=0 x=((−5±(√(25−16)))/4) =((−5±3)/4)=−(1/2),−2 ^((A)) x+(1/x)=±((i(√5))/2)⇒ { ((2x^2 −i(√5) x+2=0)),((2x^2 +i(√5) x+2=0)) :} 2x^2 −i(√5) x+2=0 ∣ 2x^2 +i(√5) x+2=0 x=((i(√5) ±(√(−5−16)))/4) ∣ x=((−i(√5) ±(√(−5−16)))/4) x=((i(√5) ±i(√(21)))/4) ∣ x=((−i(√5) ±i(√(21)))/4) x=((i((√5) ±(√(21)) ))/4) ∣ x=((i(−(√5) ±(√(21)) ))/4) These also may be valid solutions.
$$\frac{{x}^{\mathrm{11}} +{x}}{{x}^{\mathrm{7}} +{x}^{\mathrm{5}} }\:=\:\frac{\mathrm{205}}{\mathrm{16}} \\ $$$$\frac{\:\:\frac{{x}^{\mathrm{11}} +{x}}{{x}^{\mathrm{6}} }\:\:}{\frac{{x}^{\mathrm{7}} +{x}^{\mathrm{5}} }{{x}^{\mathrm{6}} }}=\frac{\mathrm{205}}{\mathrm{16}} \\ $$$$\frac{{x}^{\mathrm{5}} +\frac{\mathrm{1}}{{x}^{\mathrm{5}} }}{{x}+\frac{\mathrm{1}}{{x}}}=\frac{\mathrm{205}}{\mathrm{16}} \\ $$$${x}+\frac{\mathrm{1}}{{x}}={u} \\ $$$$\left({x}+\frac{\mathrm{1}}{{x}}\right)^{\mathrm{3}} ={u}^{\mathrm{3}} \\ $$$${x}^{\mathrm{3}} +\frac{\mathrm{1}}{{x}^{\mathrm{3}} }+\mathrm{3}\left({x}+\frac{\mathrm{1}}{{x}}\right)={u}^{\mathrm{3}} \\ $$$${x}^{\mathrm{3}} +\frac{\mathrm{1}}{{x}^{\mathrm{3}} }={u}^{\mathrm{3}} −\mathrm{3}{u}…………..\left({i}\right) \\ $$$$\left({x}+\frac{\mathrm{1}}{{x}}\right)^{\mathrm{2}} ={u}^{\mathrm{2}} \\ $$$${x}^{\mathrm{2}} +\frac{\mathrm{1}}{{x}^{\mathrm{2}} }={u}^{\mathrm{2}} −\mathrm{2}…………….\left({ii}\right) \\ $$$$\left({i}\right)×\left({ii}\right): \\ $$$${x}^{\mathrm{5}} +\frac{\mathrm{1}}{{x}^{\mathrm{5}} }+{x}+\frac{\mathrm{1}}{{x}}={u}^{\mathrm{5}} −\mathrm{3}{u}^{\mathrm{3}} −\mathrm{2}{u}^{\mathrm{3}} +\mathrm{6}{u} \\ $$$${x}^{\mathrm{5}} +\frac{\mathrm{1}}{{x}^{\mathrm{5}} }={u}^{\mathrm{5}} −\mathrm{5}{u}^{\mathrm{3}} +\mathrm{5}{u} \\ $$$$\frac{{u}^{\mathrm{5}} −\mathrm{5}{u}^{\mathrm{3}} +\mathrm{5}{u}}{{u}}=\frac{\mathrm{205}}{\mathrm{16}} \\ $$$${u}^{\mathrm{4}} −\mathrm{5}{u}^{\mathrm{2}} +\mathrm{5}−\frac{\mathrm{205}}{\mathrm{16}}=\mathrm{0} \\ $$$$\mathrm{16}{u}^{\mathrm{4}} −\mathrm{80}{u}^{\mathrm{2}} −\mathrm{125}=\mathrm{0} \\ $$$${u}^{\mathrm{2}} =\frac{\mathrm{80}\pm\sqrt{\mathrm{6400}+\mathrm{8000}}}{\mathrm{32}}=\frac{\mathrm{80}\pm\mathrm{120}}{\mathrm{32}}=\frac{\mathrm{25}}{\mathrm{4}},−\frac{\mathrm{5}}{\mathrm{4}} \\ $$$${u}=\pm\frac{\mathrm{5}}{\mathrm{2}},\pm\frac{{i}\sqrt{\mathrm{5}}}{\mathrm{2}} \\ $$$${x}+\frac{\mathrm{1}}{{x}}=\pm\frac{\mathrm{5}}{\mathrm{2}}\:\:\mid\:{x}+\frac{\mathrm{1}}{{x}}=\pm\frac{{i}\sqrt{\mathrm{5}}}{\mathrm{2}}\:^{\left(\mathrm{A}\right)} \\ $$$$\mathrm{2}{x}^{\mathrm{2}} +\mathrm{2}=\pm\mathrm{5}{x}\: \\ $$$$\begin{cases}{\mathrm{2}{x}^{\mathrm{2}} +\mathrm{2}=\mathrm{5}{x}\Rightarrow\mathrm{2}{x}^{\mathrm{2}} −\mathrm{5}{x}+\mathrm{2}=\mathrm{0}^{\bullet} }\\{\mathrm{2}{x}^{\mathrm{2}} +\mathrm{2}=−\mathrm{5}{x}\Rightarrow\mathrm{2}{x}^{\mathrm{2}} +\mathrm{5}{x}+\mathrm{2}=\mathrm{0}^{\bullet\bullet} }\end{cases} \\ $$$$\:^{\bullet} \mathrm{2}{x}^{\mathrm{2}} −\mathrm{5}{x}+\mathrm{2}=\mathrm{0}\: \\ $$$${x}=\frac{\mathrm{5}\pm\sqrt{\mathrm{25}−\mathrm{16}}}{\mathrm{4}}\: \\ $$$$\:\:\:\:=\frac{\mathrm{5}\pm\mathrm{3}}{\mathrm{4}}=\mathrm{2},\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\:^{\bullet\bullet} \mathrm{2}{x}^{\mathrm{2}} +\mathrm{5}{x}+\mathrm{2}=\mathrm{0} \\ $$$$\:\:{x}=\frac{−\mathrm{5}\pm\sqrt{\mathrm{25}−\mathrm{16}}}{\mathrm{4}} \\ $$$$\:\:\:\:\:\:=\frac{−\mathrm{5}\pm\mathrm{3}}{\mathrm{4}}=−\frac{\mathrm{1}}{\mathrm{2}},−\mathrm{2} \\ $$$$ \\ $$$$\:^{\left(\mathrm{A}\right)} \:{x}+\frac{\mathrm{1}}{{x}}=\pm\frac{{i}\sqrt{\mathrm{5}}}{\mathrm{2}}\Rightarrow\begin{cases}{\mathrm{2}{x}^{\mathrm{2}} −{i}\sqrt{\mathrm{5}}\:{x}+\mathrm{2}=\mathrm{0}}\\{\mathrm{2}{x}^{\mathrm{2}} +{i}\sqrt{\mathrm{5}}\:{x}+\mathrm{2}=\mathrm{0}}\end{cases} \\ $$$$\mathrm{2}{x}^{\mathrm{2}} −{i}\sqrt{\mathrm{5}}\:{x}+\mathrm{2}=\mathrm{0}\:\mid\:\mathrm{2}{x}^{\mathrm{2}} +{i}\sqrt{\mathrm{5}}\:{x}+\mathrm{2}=\mathrm{0} \\ $$$${x}=\frac{{i}\sqrt{\mathrm{5}}\:\pm\sqrt{−\mathrm{5}−\mathrm{16}}}{\mathrm{4}}\:\mid\:{x}=\frac{−{i}\sqrt{\mathrm{5}}\:\pm\sqrt{−\mathrm{5}−\mathrm{16}}}{\mathrm{4}} \\ $$$${x}=\frac{{i}\sqrt{\mathrm{5}}\:\pm{i}\sqrt{\mathrm{21}}}{\mathrm{4}}\:\mid\:{x}=\frac{−{i}\sqrt{\mathrm{5}}\:\pm{i}\sqrt{\mathrm{21}}}{\mathrm{4}} \\ $$$${x}=\frac{{i}\left(\sqrt{\mathrm{5}}\:\pm\sqrt{\mathrm{21}}\:\right)}{\mathrm{4}}\:\mid\:{x}=\frac{{i}\left(−\sqrt{\mathrm{5}}\:\pm\sqrt{\mathrm{21}}\:\right)}{\mathrm{4}} \\ $$$$\mathcal{T}{hese}\:{also}\:\boldsymbol{{may}}\:\boldsymbol{{be}}\:{valid}\:{solutions}. \\ $$
Commented by BaliramKumar last updated on 11/Sep/22
x = ((±5±3)/4) x = ((5+3)/4) = 2 x = ((−5−3)/4) = −2 x = ((5−3)/4) = (1/2) x = ((−5+3)/4) = − (1/2)
$${x}\:=\:\frac{\pm\mathrm{5}\pm\mathrm{3}}{\mathrm{4}} \\ $$$${x}\:=\:\frac{\mathrm{5}+\mathrm{3}}{\mathrm{4}}\:=\:\mathrm{2} \\ $$$${x}\:=\:\frac{−\mathrm{5}−\mathrm{3}}{\mathrm{4}}\:=\:−\mathrm{2} \\ $$$${x}\:=\:\frac{\mathrm{5}−\mathrm{3}}{\mathrm{4}}\:=\:\frac{\mathrm{1}}{\mathrm{2}} \\ $$$${x}\:=\:\frac{−\mathrm{5}+\mathrm{3}}{\mathrm{4}}\:=\:−\:\frac{\mathrm{1}}{\mathrm{2}} \\ $$
Commented by Rasheed.Sindhi last updated on 11/Sep/22
Thank you Baliram, I′ve added the solutions: x=(1/2),x=−(1/2) now. Please revisit my answer.
$$\mathcal{T}{hank}\:{you}\:{Baliram},\:{I}'{ve}\:{added} \\ $$$${the}\:{solutions}:\:{x}=\frac{\mathrm{1}}{\mathrm{2}},{x}=−\frac{\mathrm{1}}{\mathrm{2}}\:{now}. \\ $$$${Please}\:{revisit}\:{my}\:{answer}. \\ $$
Commented by BaliramKumar last updated on 11/Sep/22
I check the answers by Hiper scientific calculator App ✓
$${I}\:{check}\:{the}\:{answers}\:{by}\:{Hiper}\:{scientific}\:{calculator}\:{App}\:\checkmark \\ $$
Commented by Rasheed.Sindhi last updated on 11/Sep/22
������
Commented by Tawa11 last updated on 15/Sep/22
Great sir
$$\mathrm{Great}\:\mathrm{sir} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *