Question Number 92179 by otchereabdullai@gmail.com last updated on 05/May/20
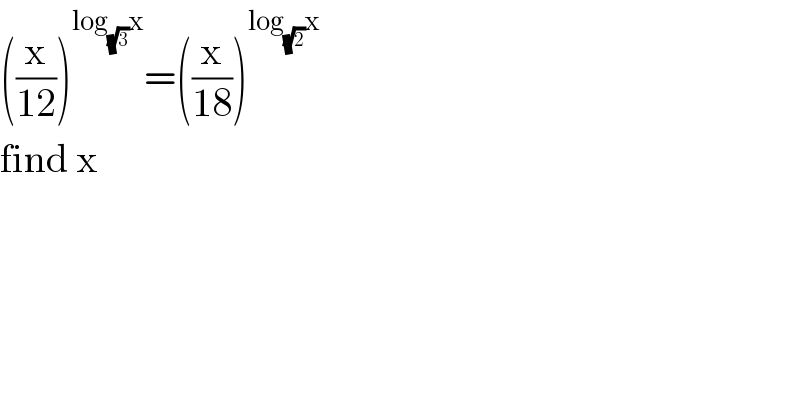
Commented by john santu last updated on 05/May/20
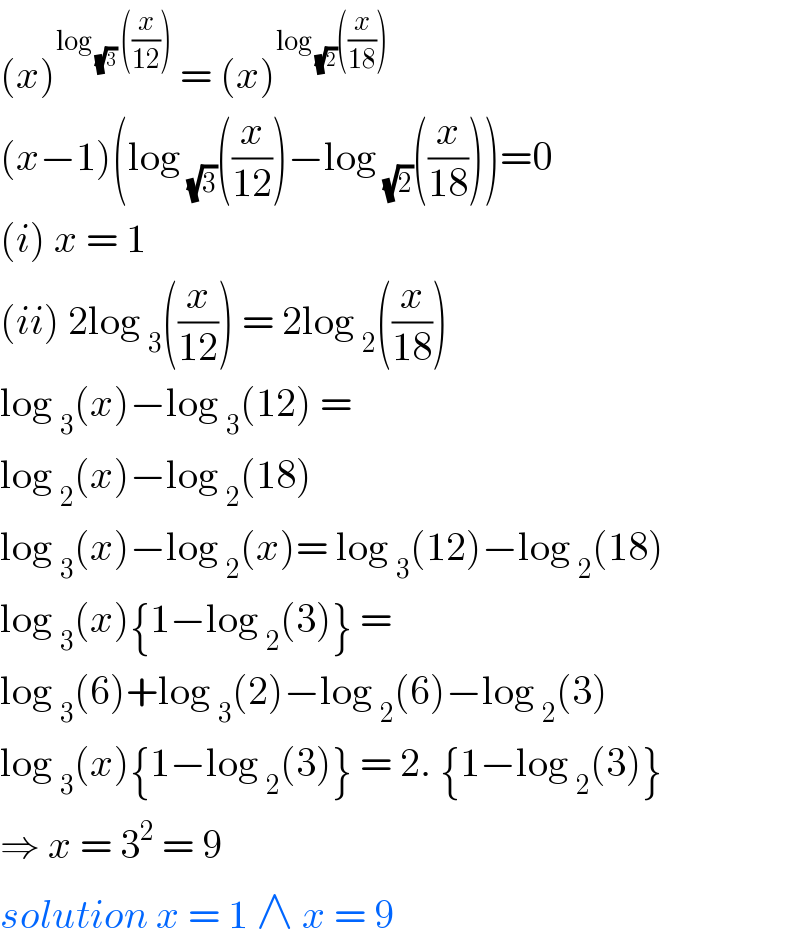
Commented by jagoll last updated on 05/May/20
good 







Commented by otchereabdullai@gmail.com last updated on 05/May/20
Commented by otchereabdullai@gmail.com last updated on 05/May/20

Commented by otchereabdullai@gmail.com last updated on 05/May/20

Commented by otchereabdullai@gmail.com last updated on 05/May/20

Commented by john santu last updated on 05/May/20

Commented by john santu last updated on 05/May/20
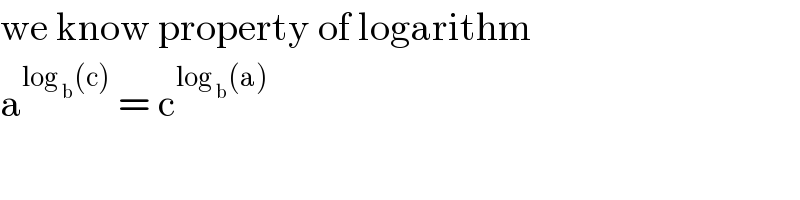
Commented by john santu last updated on 05/May/20
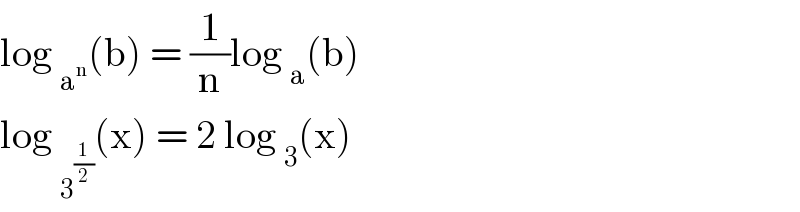
Commented by otchereabdullai@gmail.com last updated on 05/May/20
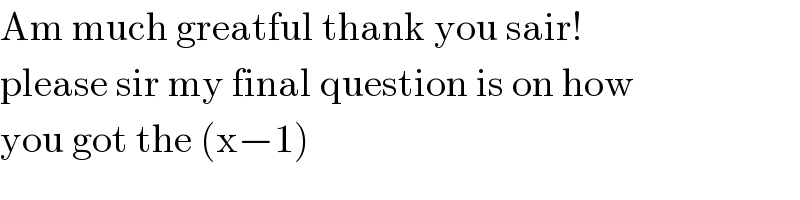
Commented by jagoll last updated on 05/May/20
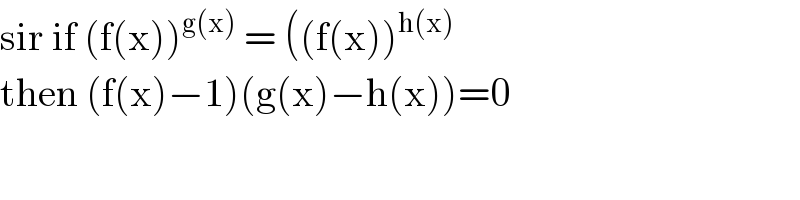
Commented by otchereabdullai@gmail.com last updated on 05/May/20

