Question Number 53108 by Tawa1 last updated on 17/Jan/19
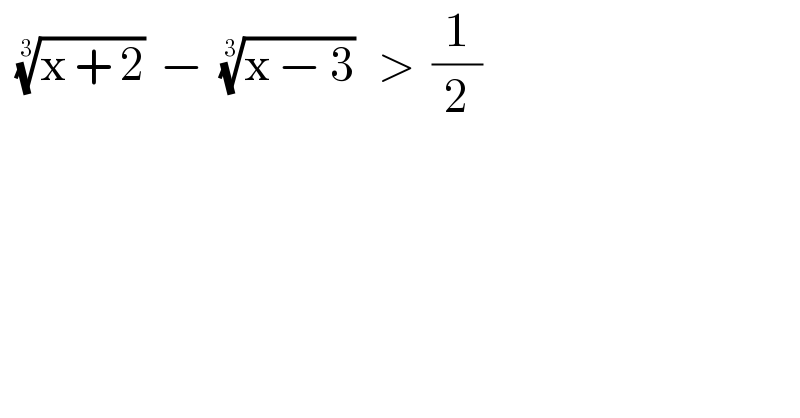
$$\:\:\sqrt[{\mathrm{3}}]{\mathrm{x}\:+\:\mathrm{2}}\:\:−\:\:\sqrt[{\mathrm{3}}]{\mathrm{x}\:−\:\mathrm{3}}\:\:\:>\:\:\frac{\mathrm{1}}{\mathrm{2}} \\ $$
Answered by kaivan.ahmadi last updated on 17/Jan/19
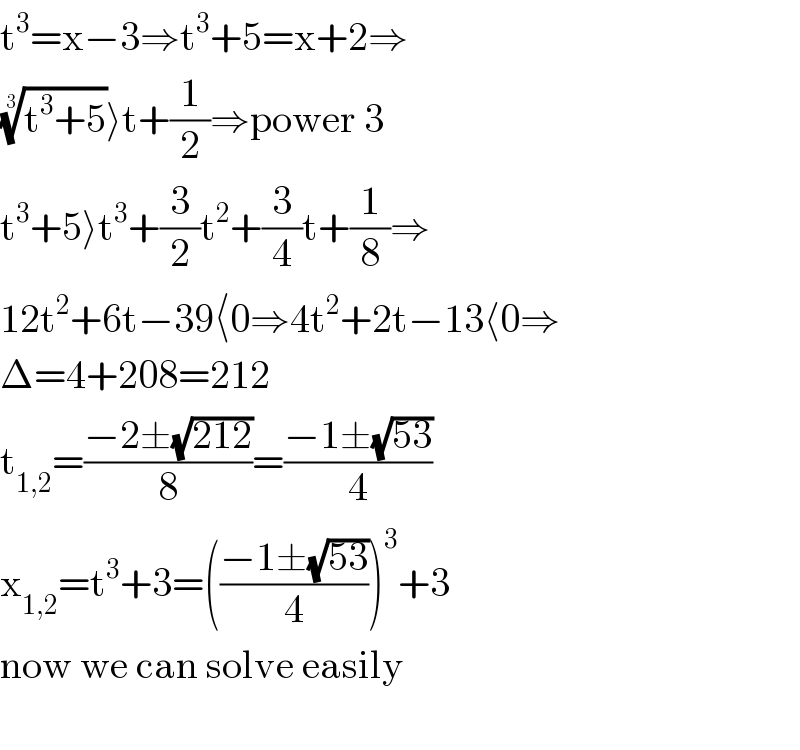
$$\mathrm{t}^{\mathrm{3}} =\mathrm{x}−\mathrm{3}\Rightarrow\mathrm{t}^{\mathrm{3}} +\mathrm{5}=\mathrm{x}+\mathrm{2}\Rightarrow \\ $$$$\sqrt[{\mathrm{3}}]{\mathrm{t}^{\mathrm{3}} +\mathrm{5}}\rangle\mathrm{t}+\frac{\mathrm{1}}{\mathrm{2}}\Rightarrow\mathrm{power}\:\mathrm{3} \\ $$$$\mathrm{t}^{\mathrm{3}} +\mathrm{5}\rangle\mathrm{t}^{\mathrm{3}} +\frac{\mathrm{3}}{\mathrm{2}}\mathrm{t}^{\mathrm{2}} +\frac{\mathrm{3}}{\mathrm{4}}\mathrm{t}+\frac{\mathrm{1}}{\mathrm{8}}\Rightarrow \\ $$$$\mathrm{12t}^{\mathrm{2}} +\mathrm{6t}−\mathrm{39}\langle\mathrm{0}\Rightarrow\mathrm{4t}^{\mathrm{2}} +\mathrm{2t}−\mathrm{13}\langle\mathrm{0}\Rightarrow \\ $$$$\Delta=\mathrm{4}+\mathrm{208}=\mathrm{212} \\ $$$$\mathrm{t}_{\mathrm{1},\mathrm{2}} =\frac{−\mathrm{2}\pm\sqrt{\mathrm{212}}}{\mathrm{8}}=\frac{−\mathrm{1}\pm\sqrt{\mathrm{53}}}{\mathrm{4}} \\ $$$$\mathrm{x}_{\mathrm{1},\mathrm{2}} =\mathrm{t}^{\mathrm{3}} +\mathrm{3}=\left(\frac{−\mathrm{1}\pm\sqrt{\mathrm{53}}}{\mathrm{4}}\right)^{\mathrm{3}} +\mathrm{3} \\ $$$$\mathrm{now}\:\mathrm{we}\:\mathrm{can}\:\mathrm{solve}\:\mathrm{easily} \\ $$$$ \\ $$
Commented by Tawa1 last updated on 18/Jan/19

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}\: \\ $$
