Question Number 122875 by pipin last updated on 20/Nov/20

$$\:\int\frac{\left(\boldsymbol{\mathrm{x}}^{\mathrm{2}} +\mathrm{1}\right)\boldsymbol{\mathrm{dx}}}{\boldsymbol{\mathrm{x}}^{\mathrm{4}} +\boldsymbol{\mathrm{x}}^{\mathrm{2}} +\mathrm{1}}\:=\:… \\ $$$$\: \\ $$
Answered by som(math1967) last updated on 20/Nov/20
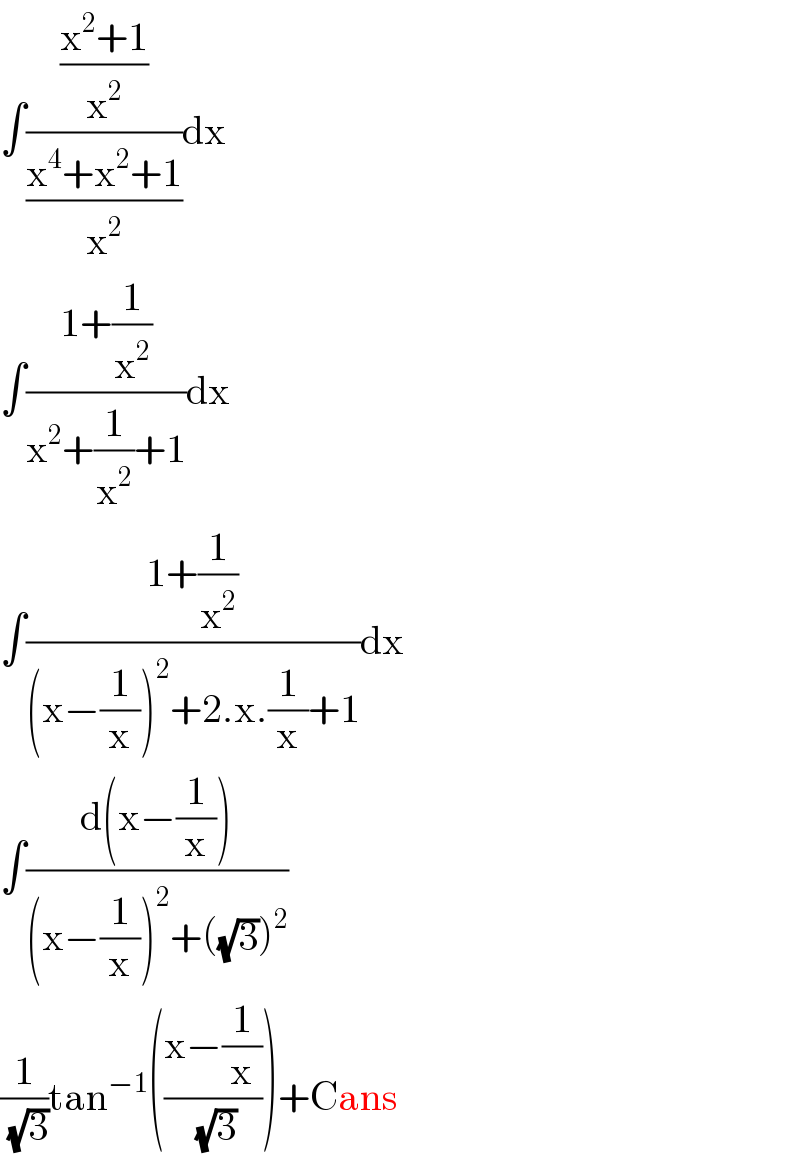
$$\int\frac{\frac{\mathrm{x}^{\mathrm{2}} +\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }}{\frac{\mathrm{x}^{\mathrm{4}} +\mathrm{x}^{\mathrm{2}} +\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }}\mathrm{dx} \\ $$$$\int\frac{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }}{\mathrm{x}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }+\mathrm{1}}\mathrm{dx} \\ $$$$\int\frac{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }}{\left(\mathrm{x}−\frac{\mathrm{1}}{\mathrm{x}}\right)^{\mathrm{2}} +\mathrm{2}.\mathrm{x}.\frac{\mathrm{1}}{\mathrm{x}}+\mathrm{1}}\mathrm{dx} \\ $$$$\int\frac{\mathrm{d}\left(\mathrm{x}−\frac{\mathrm{1}}{\mathrm{x}}\right)}{\left(\mathrm{x}−\frac{\mathrm{1}}{\mathrm{x}}\right)^{\mathrm{2}} +\left(\sqrt{\mathrm{3}}\right)^{\mathrm{2}} } \\ $$$$\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{x}−\frac{\mathrm{1}}{\mathrm{x}}}{\:\sqrt{\mathrm{3}}}\right)+\mathrm{Cans} \\ $$
Commented by pipin last updated on 20/Nov/20

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{very}\:\mathrm{much}\:\mathrm{sir} \\ $$
Commented by som(math1967) last updated on 20/Nov/20

$$\mathrm{welcome} \\ $$
