Menu Close

x-2-1-x-1-2-2017yz-y-2-1-y-1-2-2017xz-z-2-1-z-1-2-2017xy-x-1-y-1-z-1-prove-that-x-y-z-1-2018-2015-2-2018-2-

Tinku Tara 0 Comments
Pin




Question Number 106233 by malwaan last updated on 03/Aug/20
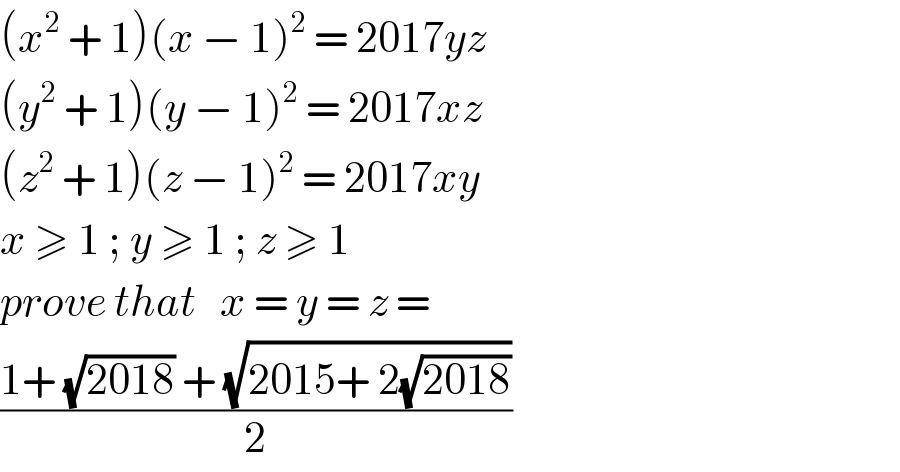
(x^2 + 1)(x − 1)^2 = 2017yz (y^2 + 1)(y − 1)^2 = 2017xz (z^2 + 1)(z − 1)^2 = 2017xy x ≥ 1 ; y ≥ 1 ; z ≥ 1 prove that x = y = z = ((1+ (√(2018)) + (√(2015+ 2(√(2018)))))/2)
$$\left({x}^{\mathrm{2}} \:+\:\mathrm{1}\right)\left({x}\:−\:\mathrm{1}\right)^{\mathrm{2}} \:=\:\mathrm{2017}{yz} \\ $$$$\left({y}^{\mathrm{2}} \:+\:\mathrm{1}\right)\left({y}\:−\:\mathrm{1}\right)^{\mathrm{2}} \:=\:\mathrm{2017}{xz} \\ $$$$\left({z}^{\mathrm{2}} \:+\:\mathrm{1}\right)\left({z}\:−\:\mathrm{1}\right)^{\mathrm{2}} \:=\:\mathrm{2017}{xy} \\ $$$${x}\:\geqslant\:\mathrm{1}\:;\:{y}\:\geqslant\:\mathrm{1}\:;\:{z}\:\geqslant\:\mathrm{1} \\ $$$${prove}\:{that}\:\:\:{x}\:=\:{y}\:=\:{z}\:= \\ $$$$\frac{\mathrm{1}+\:\sqrt{\mathrm{2018}}\:+\:\sqrt{\mathrm{2015}+\:\mathrm{2}\sqrt{\mathrm{2018}}}}{\mathrm{2}} \\ $$
Answered by Her_Majesty last updated on 04/Aug/20
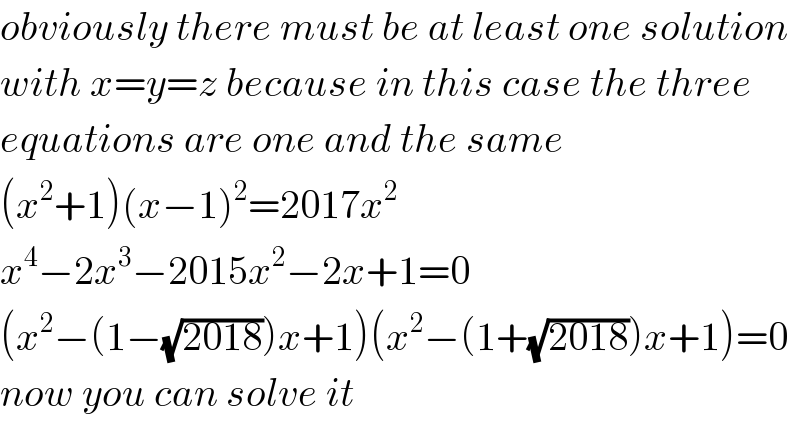
obviously there must be at least one solution with x=y=z because in this case the three equations are one and the same (x^2 +1)(x−1)^2 =2017x^2 x^4 −2x^3 −2015x^2 −2x+1=0 (x^2 −(1−(√(2018)))x+1)(x^2 −(1+(√(2018)))x+1)=0 now you can solve it
$${obviously}\:{there}\:{must}\:{be}\:{at}\:{least}\:{one}\:{solution} \\ $$$${with}\:{x}={y}={z}\:{because}\:{in}\:{this}\:{case}\:{the}\:{three} \\ $$$${equations}\:{are}\:{one}\:{and}\:{the}\:{same} \\ $$$$\left({x}^{\mathrm{2}} +\mathrm{1}\right)\left({x}−\mathrm{1}\right)^{\mathrm{2}} =\mathrm{2017}{x}^{\mathrm{2}} \\ $$$${x}^{\mathrm{4}} −\mathrm{2}{x}^{\mathrm{3}} −\mathrm{2015}{x}^{\mathrm{2}} −\mathrm{2}{x}+\mathrm{1}=\mathrm{0} \\ $$$$\left({x}^{\mathrm{2}} −\left(\mathrm{1}−\sqrt{\mathrm{2018}}\right){x}+\mathrm{1}\right)\left({x}^{\mathrm{2}} −\left(\mathrm{1}+\sqrt{\mathrm{2018}}\right){x}+\mathrm{1}\right)=\mathrm{0} \\ $$$${now}\:{you}\:{can}\:{solve}\:{it} \\ $$
Commented by Sarah85 last updated on 04/Aug/20
you learn fast it seems
Commented by Her_Majesty last updated on 04/Aug/20
I forgot more than you′ll ever know...
$${I}\:{forgot}\:{more}\:{than}\:{you}'{ll}\:{ever}\:{know}… \\ $$
Commented by malwaan last updated on 04/Aug/20
thank you but how you factor the quartic equation which has 4 solutions only one is correct ?
$${thank}\:{you} \\ $$$${but}\:{how}\:{you}\:{factor}\:\:{the}\:{quartic}\: \\ $$$${equation}\:{which}\:{has}\:\mathrm{4}\:{solutions} \\ $$$${only}\:{one}\:{is}\:{correct}\:? \\ $$
Commented by Her_Majesty last updated on 04/Aug/20
(I) x^4 +ax^3 +bx^2 +cx+d=0 x=t−(a/4) leads to t^4 +pt^2 +qt+r=0 (t^2 −αt−β)(t^2 +αt−γ)=0 t^4 −(α^2 +β+γ)t^2 +(α−β)γt+βγ=0 { ((−(α^2 +β+γ)=p)),(((α−β)γ=q)),((βγ=r)) :} solving 2 of these for β and γ we get a 3^(rd) degree polynome for α^2 (α^2 )^3 +j(α^2 )^2 +k(α^2 )+l=0 if this has a useable solution we can find the square factors of (I)
$$\left({I}\right)\:{x}^{\mathrm{4}} +{ax}^{\mathrm{3}} +{bx}^{\mathrm{2}} +{cx}+{d}=\mathrm{0} \\ $$$${x}={t}−\frac{{a}}{\mathrm{4}}\:{leads}\:{to} \\ $$$${t}^{\mathrm{4}} +{pt}^{\mathrm{2}} +{qt}+{r}=\mathrm{0} \\ $$$$\left({t}^{\mathrm{2}} −\alpha{t}−\beta\right)\left({t}^{\mathrm{2}} +\alpha{t}−\gamma\right)=\mathrm{0} \\ $$$${t}^{\mathrm{4}} −\left(\alpha^{\mathrm{2}} +\beta+\gamma\right){t}^{\mathrm{2}} +\left(\alpha−\beta\right)\gamma{t}+\beta\gamma=\mathrm{0} \\ $$$$\begin{cases}{−\left(\alpha^{\mathrm{2}} +\beta+\gamma\right)={p}}\\{\left(\alpha−\beta\right)\gamma={q}}\\{\beta\gamma={r}}\end{cases} \\ $$$${solving}\:\mathrm{2}\:{of}\:{these}\:{for}\:\beta\:{and}\:\gamma\:{we}\:{get}\:{a}\:\mathrm{3}^{{rd}} \:{degree} \\ $$$${polynome}\:{for}\:\alpha^{\mathrm{2}} \\ $$$$\left(\alpha^{\mathrm{2}} \right)^{\mathrm{3}} +{j}\left(\alpha^{\mathrm{2}} \right)^{\mathrm{2}} +{k}\left(\alpha^{\mathrm{2}} \right)+{l}=\mathrm{0} \\ $$$${if}\:{this}\:{has}\:{a}\:{useable}\:{solution}\:{we}\:{can}\:{find}\:{the} \\ $$$${square}\:{factors}\:{of}\:\left({I}\right) \\ $$
Commented by malwaan last updated on 05/Aug/20
I used another method long but easy
$${I}\:{used}\:{another}\:{method} \\ $$$${long}\:{but}\:{easy} \\ $$
Answered by malwaan last updated on 05/Aug/20
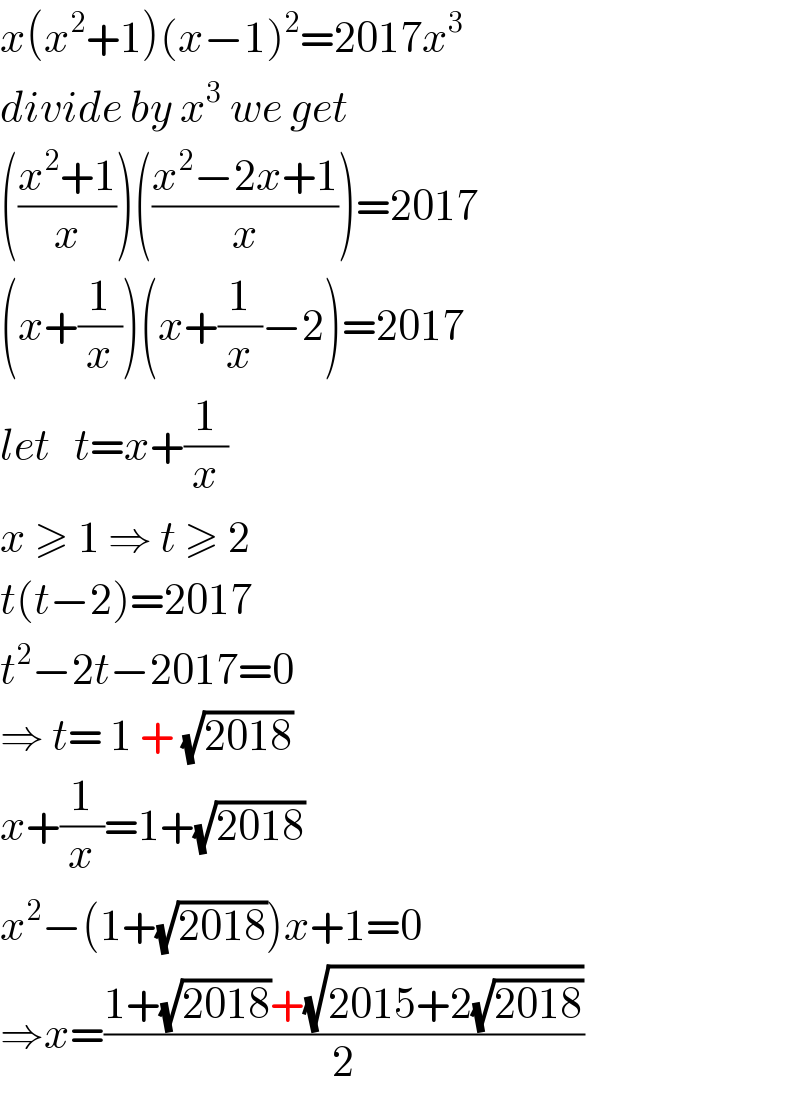
x(x^2 +1)(x−1)^2 =2017x^3 divide by x^3 we get (((x^2 +1)/x))(((x^2 −2x+1)/x))=2017 (x+(1/x))(x+(1/x)−2)=2017 let t=x+(1/x) x ≥ 1 ⇒ t ≥ 2 t(t−2)=2017 t^2 −2t−2017=0 ⇒ t= 1 + (√(2018)) x+(1/x)=1+(√(2018)) x^2 −(1+(√(2018)))x+1=0 ⇒x=((1+(√(2018))+(√(2015+2(√(2018)))))/2)
$${x}\left({x}^{\mathrm{2}} +\mathrm{1}\right)\left({x}−\mathrm{1}\right)^{\mathrm{2}} =\mathrm{2017}{x}^{\mathrm{3}} \\ $$$${divide}\:{by}\:{x}^{\mathrm{3}} \:{we}\:{get} \\ $$$$\left(\frac{{x}^{\mathrm{2}} +\mathrm{1}}{{x}}\right)\left(\frac{{x}^{\mathrm{2}} −\mathrm{2}{x}+\mathrm{1}}{{x}}\right)=\mathrm{2017} \\ $$$$\left({x}+\frac{\mathrm{1}}{{x}}\right)\left({x}+\frac{\mathrm{1}}{{x}}−\mathrm{2}\right)=\mathrm{2017} \\ $$$${let}\:\:\:{t}={x}+\frac{\mathrm{1}}{{x}} \\ $$$${x}\:\geqslant\:\mathrm{1}\:\Rightarrow\:{t}\:\geqslant\:\mathrm{2} \\ $$$${t}\left({t}−\mathrm{2}\right)=\mathrm{2017} \\ $$$${t}^{\mathrm{2}} −\mathrm{2}{t}−\mathrm{2017}=\mathrm{0} \\ $$$$\Rightarrow\:{t}=\:\mathrm{1}\:+\:\sqrt{\mathrm{2018}} \\ $$$${x}+\frac{\mathrm{1}}{{x}}=\mathrm{1}+\sqrt{\mathrm{2018}} \\ $$$${x}^{\mathrm{2}} −\left(\mathrm{1}+\sqrt{\mathrm{2018}}\right){x}+\mathrm{1}=\mathrm{0} \\ $$$$\Rightarrow{x}=\frac{\mathrm{1}+\sqrt{\mathrm{2018}}+\sqrt{\mathrm{2015}+\mathrm{2}\sqrt{\mathrm{2018}}}}{\mathrm{2}} \\ $$
Commented by Her_Majesty last updated on 05/Aug/20
good!
$${good}! \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *