Question Number 86246 by Rio Michael last updated on 27/Mar/20
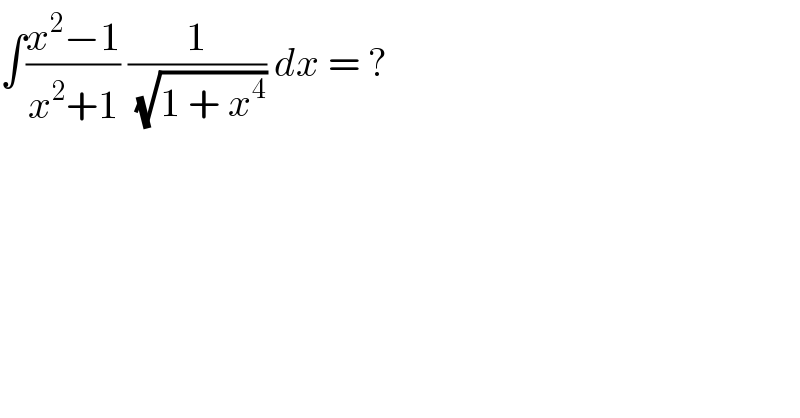
$$\int\frac{{x}^{\mathrm{2}} −\mathrm{1}}{{x}^{\mathrm{2}} +\mathrm{1}}\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}\:+\:{x}^{\mathrm{4}} }}\:{dx}\:=\:? \\ $$
Answered by TANMAY PANACEA. last updated on 27/Mar/20

$$\int\frac{\mathrm{1}−\frac{\mathrm{1}}{{x}^{\mathrm{2}} }}{\mathrm{1}+\frac{\mathrm{1}}{{x}^{\mathrm{2}} }}×\frac{\mathrm{1}}{{x}\sqrt{{x}^{\mathrm{2}} +\frac{\mathrm{1}}{{x}^{\mathrm{2}} }}}{dx} \\ $$$$\int\frac{{d}\left({x}+\frac{\mathrm{1}}{{x}}\right)}{\left({x}+\frac{\mathrm{1}}{{x}}\right)\sqrt{\left({x}+\frac{\mathrm{1}}{{x}}\right)^{\mathrm{2}} −\mathrm{2}}} \\ $$$$\int\frac{{da}}{{a}\sqrt{{a}^{\mathrm{2}} −\mathrm{2}}} \\ $$$${a}=\sqrt{\mathrm{2}}\:{sec}\theta \\ $$$$\int\frac{\sqrt{\mathrm{2}}\:{sec}\theta{tan}\theta}{\:\sqrt{\mathrm{2}}\:{sec}\theta×\sqrt{\mathrm{2}}\:{tan}\theta}{d}\theta \\ $$$$\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}{sec}^{−\mathrm{1}} \left(\frac{{a}}{\:\sqrt{\mathrm{2}}}\right)+{c} \\ $$$$\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}{sec}^{−\mathrm{1}} \left(\frac{{x}+\frac{\mathrm{1}}{{x}}}{\:\sqrt{\mathrm{2}}}\right)+{c} \\ $$$$ \\ $$
Commented by Rio Michael last updated on 27/Mar/20

$$\mathrm{thanks}\:\mathrm{sir} \\ $$
Commented by TANMAY PANACEA. last updated on 27/Mar/20

$${most}\:{welcome} \\ $$
