Question Number 35015 by NECx last updated on 14/May/18
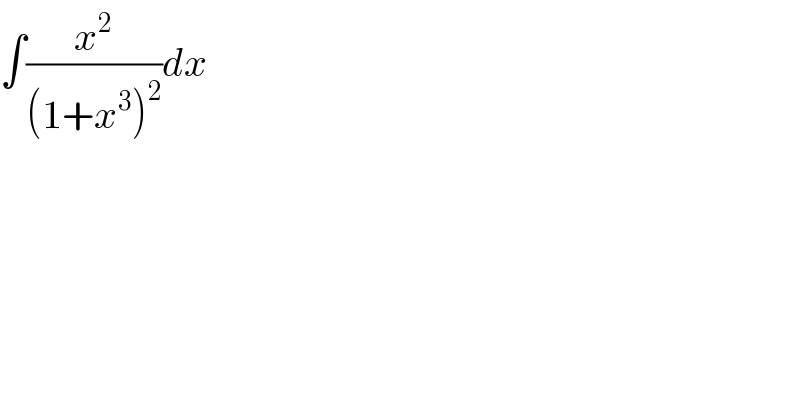
$$\int\frac{{x}^{\mathrm{2}} }{\left(\mathrm{1}+{x}^{\mathrm{3}} \right)^{\mathrm{2}} }{dx} \\ $$
Answered by ajfour last updated on 14/May/18
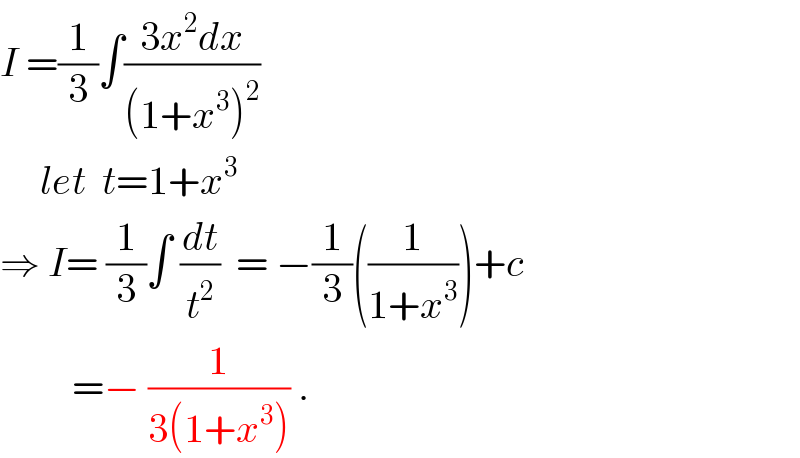
$${I}\:=\frac{\mathrm{1}}{\mathrm{3}}\int\frac{\mathrm{3}{x}^{\mathrm{2}} {dx}}{\left(\mathrm{1}+{x}^{\mathrm{3}} \right)^{\mathrm{2}} } \\ $$$$\:\:\:\:\:{let}\:\:{t}=\mathrm{1}+{x}^{\mathrm{3}} \\ $$$$\Rightarrow\:{I}=\:\frac{\mathrm{1}}{\mathrm{3}}\int\:\frac{{dt}}{{t}^{\mathrm{2}} }\:\:=\:−\frac{\mathrm{1}}{\mathrm{3}}\left(\frac{\mathrm{1}}{\mathrm{1}+{x}^{\mathrm{3}} }\right)+{c} \\ $$$$\:\:\:\:\:\:\:\:\:=−\:\frac{\mathrm{1}}{\mathrm{3}\left(\mathrm{1}+{x}^{\mathrm{3}} \right)}\:. \\ $$
Commented by NECx last updated on 15/May/18
$${thank}\:{you}\:{so}\:{much} \\ $$$$ \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 14/May/18
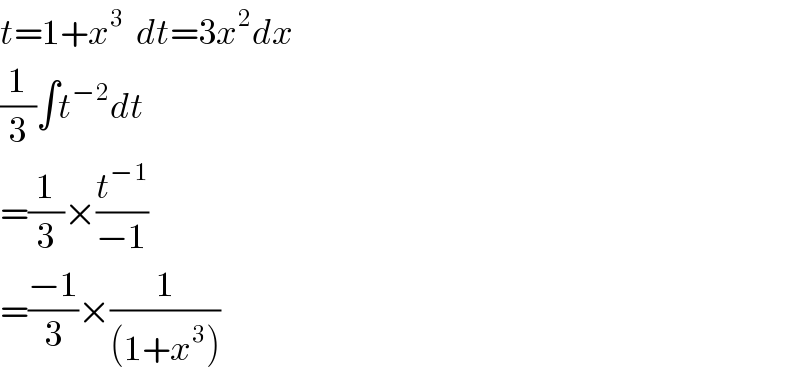
$${t}=\mathrm{1}+{x}^{\mathrm{3}} \:\:{dt}=\mathrm{3}{x}^{\mathrm{2}} {dx} \\ $$$$\frac{\mathrm{1}}{\mathrm{3}}\int{t}^{−\mathrm{2}} {dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}}×\frac{{t}^{−\mathrm{1}} }{−\mathrm{1}} \\ $$$$=\frac{−\mathrm{1}}{\mathrm{3}}×\frac{\mathrm{1}}{\left(\mathrm{1}+{x}^{\mathrm{3}} \right)} \\ $$
Commented by NECx last updated on 15/May/18
$${Thank}\:{you}\:{so}\:{much} \\ $$
