Question Number 118260 by bobhans last updated on 16/Oct/20
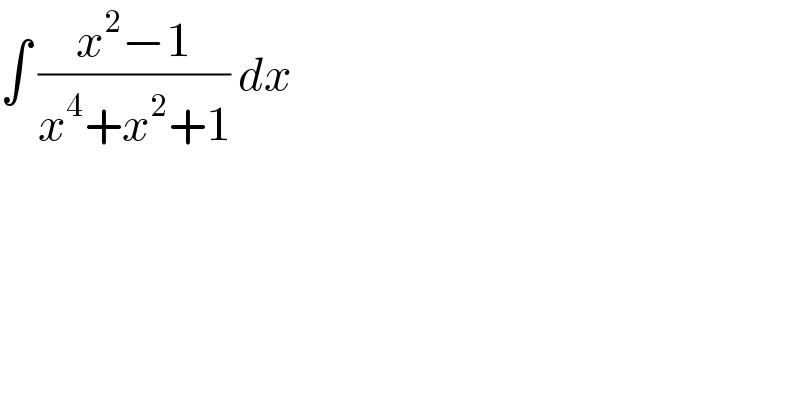
$$\int\:\frac{{x}^{\mathrm{2}} −\mathrm{1}}{{x}^{\mathrm{4}} +{x}^{\mathrm{2}} +\mathrm{1}}\:{dx} \\ $$
Commented by bobhans last updated on 16/Oct/20

$${yes}…….\:{all}\:{sir} \\ $$
Answered by som(math1967) last updated on 16/Oct/20
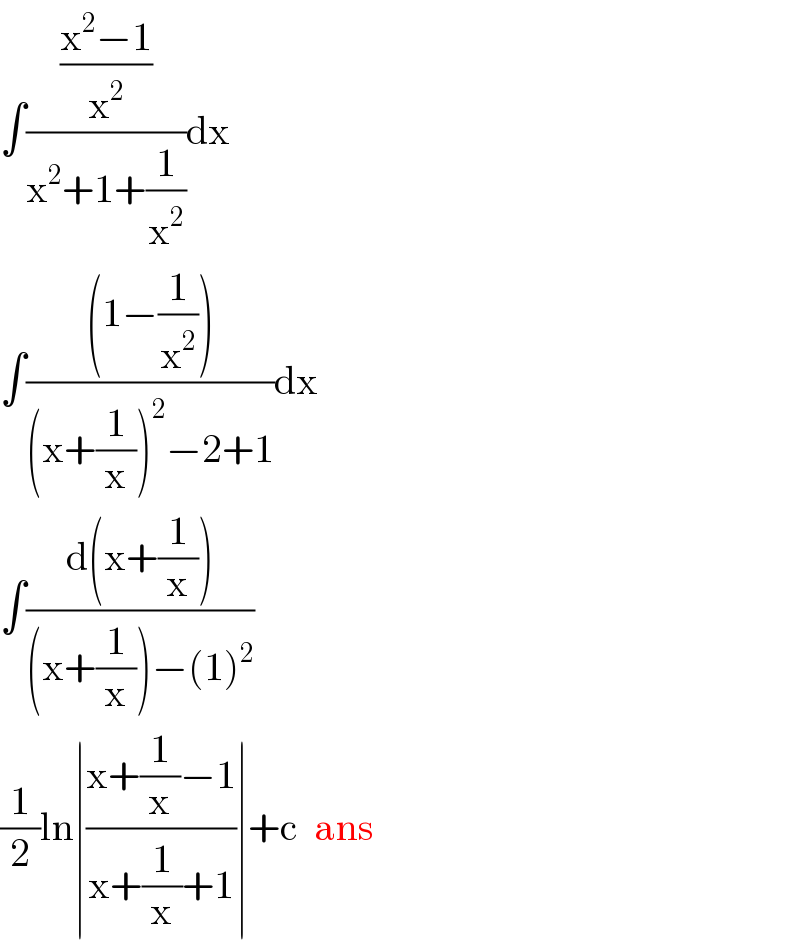
$$\int\frac{\frac{\mathrm{x}^{\mathrm{2}} −\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }}{\mathrm{x}^{\mathrm{2}} +\mathrm{1}+\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }}\mathrm{dx} \\ $$$$\int\frac{\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }\right)}{\left(\mathrm{x}+\frac{\mathrm{1}}{\mathrm{x}}\right)^{\mathrm{2}} −\mathrm{2}+\mathrm{1}}\mathrm{dx} \\ $$$$\int\frac{\mathrm{d}\left(\mathrm{x}+\frac{\mathrm{1}}{\mathrm{x}}\right)}{\left(\mathrm{x}+\frac{\mathrm{1}}{\mathrm{x}}\right)−\left(\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\mid\frac{\mathrm{x}+\frac{\mathrm{1}}{\mathrm{x}}−\mathrm{1}}{\mathrm{x}+\frac{\mathrm{1}}{\mathrm{x}}+\mathrm{1}}\mid+\mathrm{c}\:\:\mathrm{ans} \\ $$
Answered by malwaan last updated on 16/Oct/20
![∫(( x^2 − 1)/((x^4 +2x^2 +1)−x^2 )) dx =∫((x^2 −1)/((x^2 +1)^2 −x^2 ))dx =∫(( x^2 −1)/((x^2 +x+1)(x^2 −x+1))) dx ((x^2 −1)/((x^2 +x+1)(x^2 −x+1))) = ((ax+b)/(x^2 +x+1)) + ((cx+d)/(x^2 −x+1)) = ((ax^3 −ax^2 +ax+bx^2 −bx+b+cx^3 +cx^2 +cx+dx^2 +dx+d)/((x^2 +x+1)(x^2 −x+1))) a + c = 0 ............1 −a+b+c+d=1....2 a−b+c+d= 0......3 b + d =−1...........4 ⇒a = −1 ; b = − (1/2) c = 1 ; d = − (1/2) ∴ ∫ ((−x−(1/2))/(x^2 +x+1))dx + ∫((x−(1/2))/(x^2 −x+1))dx = − (1/2) ∫((2x+1)/(x^2 +x+1))dx+ (1/2)∫((2x−1)/(x^2 −x+1))dx = (1/2)[ln(x^2 −x+1)−ln(x^2 +x+1)]+ C](https://www.tinkutara.com/question/Q118266.png)
$$\int\frac{\:{x}^{\mathrm{2}} \:−\:\mathrm{1}}{\left({x}^{\mathrm{4}} +\mathrm{2}{x}^{\mathrm{2}} +\mathrm{1}\right)−{x}^{\mathrm{2}} }\:{dx} \\ $$$$=\int\frac{{x}^{\mathrm{2}} −\mathrm{1}}{\left({x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} −{x}^{\mathrm{2}} }{dx} \\ $$$$=\int\frac{\:{x}^{\mathrm{2}} −\mathrm{1}}{\left({x}^{\mathrm{2}} +{x}+\mathrm{1}\right)\left({x}^{\mathrm{2}} −{x}+\mathrm{1}\right)}\:{dx} \\ $$$$\frac{{x}^{\mathrm{2}} −\mathrm{1}}{\left({x}^{\mathrm{2}} +{x}+\mathrm{1}\right)\left({x}^{\mathrm{2}} −{x}+\mathrm{1}\right)}\:= \\ $$$$\frac{{ax}+{b}}{{x}^{\mathrm{2}} +{x}+\mathrm{1}}\:+\:\frac{{cx}+{d}}{{x}^{\mathrm{2}} −{x}+\mathrm{1}}\:= \\ $$$$\frac{{ax}^{\mathrm{3}} −{ax}^{\mathrm{2}} +{ax}+{bx}^{\mathrm{2}} −{bx}+{b}+{cx}^{\mathrm{3}} +{cx}^{\mathrm{2}} +{cx}+{dx}^{\mathrm{2}} +{dx}+{d}}{\left({x}^{\mathrm{2}} +{x}+\mathrm{1}\right)\left({x}^{\mathrm{2}} −{x}+\mathrm{1}\right)} \\ $$$${a}\:+\:{c}\:=\:\mathrm{0}\:…………\mathrm{1} \\ $$$$−{a}+{b}+{c}+{d}=\mathrm{1}….\mathrm{2} \\ $$$${a}−{b}+{c}+{d}=\:\mathrm{0}……\mathrm{3} \\ $$$${b}\:+\:{d}\:=−\mathrm{1}………..\mathrm{4} \\ $$$$\Rightarrow{a}\:=\:−\mathrm{1}\:\:;\:\:{b}\:=\:−\:\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\:{c}\:=\:\mathrm{1}\:\:;\:\:\:{d}\:=\:−\:\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\therefore\:\int\:\frac{−{x}−\frac{\mathrm{1}}{\mathrm{2}}}{{x}^{\mathrm{2}} +{x}+\mathrm{1}}{dx}\:+\:\int\frac{{x}−\frac{\mathrm{1}}{\mathrm{2}}}{{x}^{\mathrm{2}} −{x}+\mathrm{1}}{dx} \\ $$$$=\:−\:\frac{\mathrm{1}}{\mathrm{2}}\:\int\frac{\mathrm{2}{x}+\mathrm{1}}{{x}^{\mathrm{2}} +{x}+\mathrm{1}}{dx}+\:\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\mathrm{2}{x}−\mathrm{1}}{{x}^{\mathrm{2}} −{x}+\mathrm{1}}{dx} \\ $$$$=\:\frac{\mathrm{1}}{\mathrm{2}}\left[{ln}\left({x}^{\mathrm{2}} −{x}+\mathrm{1}\right)−{ln}\left({x}^{\mathrm{2}} +{x}+\mathrm{1}\right)\right]+\:{C} \\ $$
Commented by malwaan last updated on 16/Oct/20
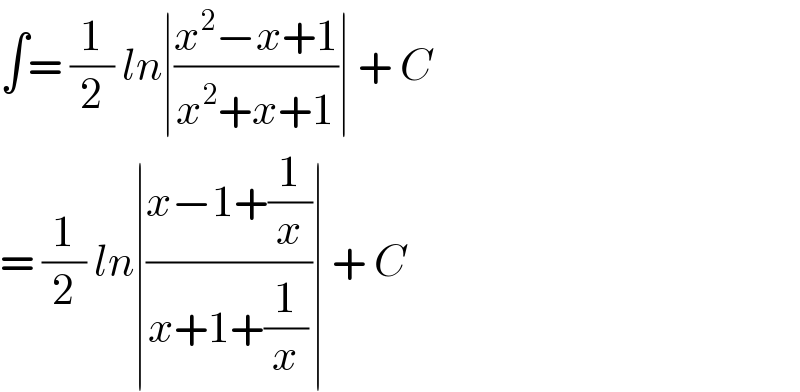
$$\int=\:\frac{\mathrm{1}}{\mathrm{2}}\:{ln}\mid\frac{{x}^{\mathrm{2}} −{x}+\mathrm{1}}{{x}^{\mathrm{2}} +{x}+\mathrm{1}}\mid\:+\:{C} \\ $$$$=\:\frac{\mathrm{1}}{\mathrm{2}}\:{ln}\mid\frac{{x}−\mathrm{1}+\frac{\mathrm{1}}{{x}}}{{x}+\mathrm{1}+\frac{\mathrm{1}}{{x}}}\mid\:+\:{C} \\ $$
Answered by bramlexs22 last updated on 16/Oct/20
![∫ ((x^2 −1)/(x^2 (x^2 +1+x^(−2) ))) dx = ∫ ((1−x^(−2) )/(x^2 +2+x^(−2) −1)) dx = ∫ ((1−x^(−2) )/((x+x^(−1) )^2 −1)) dx = [ let x+x^(−1) = v ⇒dv=1−x^(−2) dx ] ∫ (dv/(v^2 −1)) = (1/2)∫ (1/(v−1))−(1/(v+1)) dv= (1/2) ln ∣((v−1)/(v+1)) ∣ + c = ln (√((x+x^(−1) −1)/(x+x^(−1) +1))) + c](https://www.tinkutara.com/question/Q118268.png)
$$\int\:\frac{{x}^{\mathrm{2}} −\mathrm{1}}{{x}^{\mathrm{2}} \left({x}^{\mathrm{2}} +\mathrm{1}+{x}^{−\mathrm{2}} \right)}\:{dx}\:=\: \\ $$$$\int\:\frac{\mathrm{1}−{x}^{−\mathrm{2}} }{{x}^{\mathrm{2}} +\mathrm{2}+{x}^{−\mathrm{2}} −\mathrm{1}}\:{dx}\:= \\ $$$$\int\:\frac{\mathrm{1}−{x}^{−\mathrm{2}} }{\left({x}+{x}^{−\mathrm{1}} \right)^{\mathrm{2}} −\mathrm{1}}\:{dx}\:= \\ $$$$\left[\:{let}\:{x}+{x}^{−\mathrm{1}} \:=\:{v}\:\Rightarrow{dv}=\mathrm{1}−{x}^{−\mathrm{2}} \:{dx}\:\right] \\ $$$$\int\:\frac{{dv}}{{v}^{\mathrm{2}} −\mathrm{1}}\:=\:\frac{\mathrm{1}}{\mathrm{2}}\int\:\frac{\mathrm{1}}{{v}−\mathrm{1}}−\frac{\mathrm{1}}{{v}+\mathrm{1}}\:{dv}= \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\:\mathrm{ln}\:\mid\frac{{v}−\mathrm{1}}{{v}+\mathrm{1}}\:\mid\:+\:{c}\:= \\ $$$$\mathrm{ln}\:\sqrt{\frac{{x}+{x}^{−\mathrm{1}} −\mathrm{1}}{{x}+{x}^{−\mathrm{1}} +\mathrm{1}}}\:+\:{c}\: \\ $$
