Menu Close

x-2-1-y-2xy-x-x-2-1-please-solve-this-differential-equation-

Tinku Tara 0 Comments
Pin




Question Number 108475 by pticantor last updated on 17/Aug/20
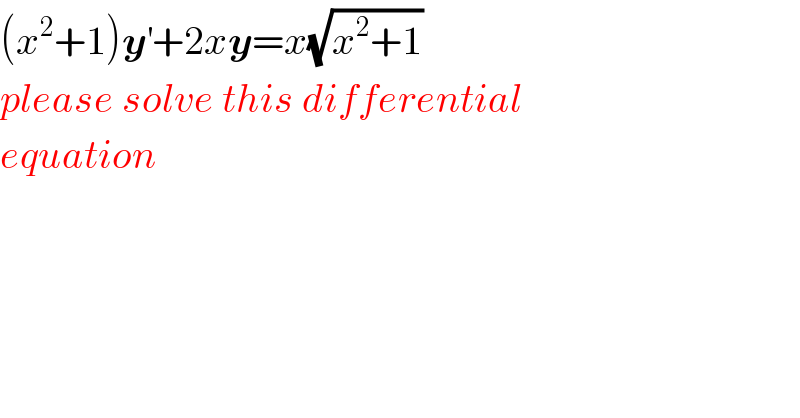
(x^2 +1)y^′ +2xy=x(√(x^2 +1)) please solve this differential equation
$$\left({x}^{\mathrm{2}} +\mathrm{1}\right)\boldsymbol{{y}}^{'} +\mathrm{2}{x}\boldsymbol{{y}}={x}\sqrt{{x}^{\mathrm{2}} +\mathrm{1}} \\ $$$${please}\:{solve}\:{this}\:{differential} \\ $$$${equation} \\ $$
Answered by Dwaipayan Shikari last updated on 17/Aug/20
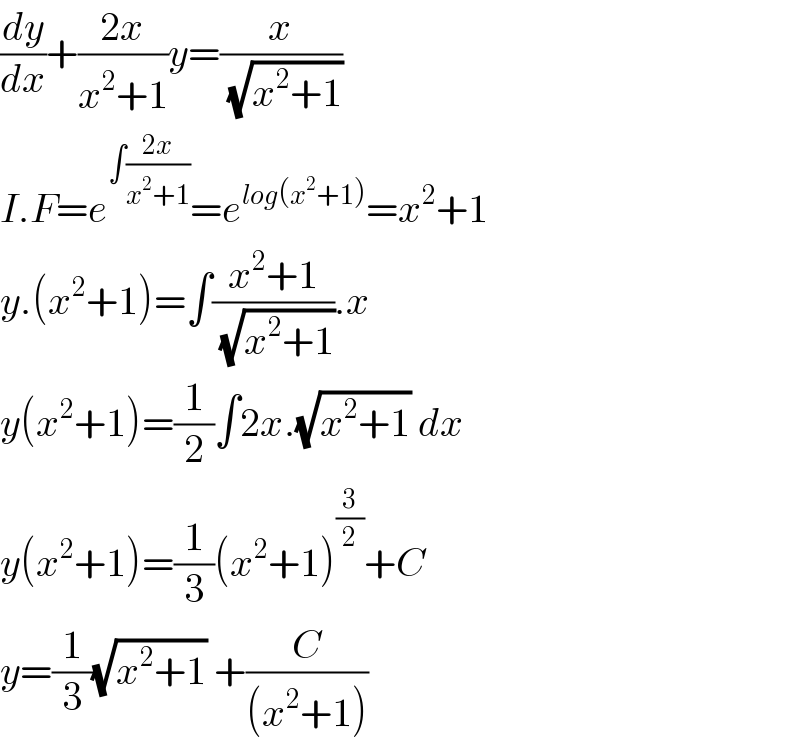
(dy/dx)+((2x)/(x^2 +1))y=(x/( (√(x^2 +1)))) I.F=e^(∫((2x)/(x^2 +1))) =e^(log(x^2 +1)) =x^2 +1 y.(x^2 +1)=∫((x^2 +1)/( (√(x^2 +1)))).x y(x^2 +1)=(1/2)∫2x.(√(x^2 +1)) dx y(x^2 +1)=(1/3)(x^2 +1)^(3/2) +C y=(1/3)(√(x^2 +1)) +(C/((x^2 +1)))
$$\frac{{dy}}{{dx}}+\frac{\mathrm{2}{x}}{{x}^{\mathrm{2}} +\mathrm{1}}{y}=\frac{{x}}{\:\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}} \\ $$$${I}.{F}={e}^{\int\frac{\mathrm{2}{x}}{{x}^{\mathrm{2}} +\mathrm{1}}} ={e}^{{log}\left({x}^{\mathrm{2}} +\mathrm{1}\right)} ={x}^{\mathrm{2}} +\mathrm{1} \\ $$$${y}.\left({x}^{\mathrm{2}} +\mathrm{1}\right)=\int\frac{{x}^{\mathrm{2}} +\mathrm{1}}{\:\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}}.{x} \\ $$$${y}\left({x}^{\mathrm{2}} +\mathrm{1}\right)=\frac{\mathrm{1}}{\mathrm{2}}\int\mathrm{2}{x}.\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}\:{dx} \\ $$$${y}\left({x}^{\mathrm{2}} +\mathrm{1}\right)=\frac{\mathrm{1}}{\mathrm{3}}\left({x}^{\mathrm{2}} +\mathrm{1}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} +{C} \\ $$$${y}=\frac{\mathrm{1}}{\mathrm{3}}\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}\:+\frac{{C}}{\left({x}^{\mathrm{2}} +\mathrm{1}\right)} \\ $$
Answered by mathmax by abdo last updated on 17/Aug/20
(x^2 +1)y^(′ ) +2xy =x(√(x^2 +1)) h→(x^2 +1)y^′ =−2xy ⇒(y^′ /y)=((−2x)/(x^2 +1)) ⇒ln∣y∣ =−ln(x^2 +1) +c ⇒ y =(k/(x^2 +1)) lagrange method ⇒y^′ =(k^′ /(x^2 +1))−((2xk)/((x^2 +1)^2 )) e ⇒k^′ −((2xk)/(x^2 +1)) +((2xk)/(x^2 +1)) =x(√(x^2 +1)) ⇒k^′ =x(√(x^2 +1)) ⇒ k (x) =∫ x(√(1+x^2 ))dx =_(x =sht) ∫ sht c^2 ht dt =(1/3)ch^3 t +c =(1/3)(((e^t +e^(−t) )/2))^3 +c =(1/(24))( e^t +e^(−t) )^(3 ) +c we have t =ln(x+(√(1+x^2 ))) ⇒ k(x) =(1/(24)){x+(√(1+x^2 )) +(1/(x+(√(1+x^2 ))))}^3 +c ⇒ y(x) =(1/(x^2 +1)){(1/(24))(x+(√(1+x^2 ))+(1/(x+(√(1+x^2 )))))^3 +c}
$$\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{1}\right)\mathrm{y}^{'\:} \:+\mathrm{2xy}\:=\mathrm{x}\sqrt{\mathrm{x}^{\mathrm{2}} \:+\mathrm{1}} \\ $$$$\mathrm{h}\rightarrow\left(\mathrm{x}^{\mathrm{2}} +\mathrm{1}\right)\mathrm{y}^{'} \:=−\mathrm{2xy}\:\Rightarrow\frac{\mathrm{y}^{'} }{\mathrm{y}}=\frac{−\mathrm{2x}}{\mathrm{x}^{\mathrm{2}} \:+\mathrm{1}}\:\Rightarrow\mathrm{ln}\mid\mathrm{y}\mid\:=−\mathrm{ln}\left(\mathrm{x}^{\mathrm{2}} +\mathrm{1}\right)\:+\mathrm{c}\:\Rightarrow \\ $$$$\mathrm{y}\:=\frac{\mathrm{k}}{\mathrm{x}^{\mathrm{2}} \:+\mathrm{1}}\:\:\mathrm{lagrange}\:\mathrm{method}\:\Rightarrow\mathrm{y}^{'} \:=\frac{\mathrm{k}^{'} }{\mathrm{x}^{\mathrm{2}} \:+\mathrm{1}}−\frac{\mathrm{2xk}}{\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$\mathrm{e}\:\Rightarrow\mathrm{k}^{'} −\frac{\mathrm{2xk}}{\mathrm{x}^{\mathrm{2}} \:+\mathrm{1}}\:+\frac{\mathrm{2xk}}{\mathrm{x}^{\mathrm{2}} \:+\mathrm{1}}\:=\mathrm{x}\sqrt{\mathrm{x}^{\mathrm{2}} \:+\mathrm{1}}\:\Rightarrow\mathrm{k}^{'} \:=\mathrm{x}\sqrt{\mathrm{x}^{\mathrm{2}} \:+\mathrm{1}}\:\Rightarrow \\ $$$$\mathrm{k}\:\left(\mathrm{x}\right)\:=\int\:\mathrm{x}\sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\mathrm{dx}\:=_{\mathrm{x}\:=\mathrm{sht}} \:\:\:\int\:\mathrm{sht}\:\mathrm{c}^{\mathrm{2}} \mathrm{ht}\:\mathrm{dt}\:\:=\frac{\mathrm{1}}{\mathrm{3}}\mathrm{ch}^{\mathrm{3}} \mathrm{t}\:\:+\mathrm{c} \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}}\left(\frac{\mathrm{e}^{\mathrm{t}} +\mathrm{e}^{−\mathrm{t}} }{\mathrm{2}}\right)^{\mathrm{3}} \:+\mathrm{c}\:=\frac{\mathrm{1}}{\mathrm{24}}\left(\:\mathrm{e}^{\mathrm{t}} \:+\mathrm{e}^{−\mathrm{t}} \right)^{\mathrm{3}\:} +\mathrm{c}\:\:\mathrm{we}\:\mathrm{have}\:\mathrm{t}\:=\mathrm{ln}\left(\mathrm{x}+\sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\right)\:\Rightarrow \\ $$$$\mathrm{k}\left(\mathrm{x}\right)\:=\frac{\mathrm{1}}{\mathrm{24}}\left\{\mathrm{x}+\sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\:+\frac{\mathrm{1}}{\mathrm{x}+\sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }}\right\}^{\mathrm{3}} \:+\mathrm{c}\:\Rightarrow \\ $$$$\mathrm{y}\left(\mathrm{x}\right)\:=\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} \:+\mathrm{1}}\left\{\frac{\mathrm{1}}{\mathrm{24}}\left(\mathrm{x}+\sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{x}+\sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }}\right)^{\mathrm{3}} \:+\mathrm{c}\right\} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *