x-2-1-y-3-5-8-11-0-find-x-and-y-

Question Number 36003 by rishijagtar@gmail.com last updated on 27/May/18

$${x}\begin{bmatrix}{\mathrm{2}}\\{\mathrm{1}}\end{bmatrix}+{y}\begin{bmatrix}{\mathrm{3}}\\{\mathrm{5}}\end{bmatrix}+\begin{bmatrix}{−\mathrm{8}}\\{−\mathrm{11}}\end{bmatrix}=\mathrm{0} \\ $$$${find}\:{x}\:{and}\:{y} \\ $$

Answered by tanmay.chaudhury50@gmail.com last updated on 27/May/18

$$\mathrm{2}{x}+\mathrm{3}{y}−\mathrm{8}=\mathrm{0} \\ $$$${x}+\mathrm{5}{y}−\mathrm{11}=\mathrm{0} \\ $$$$\mathrm{2}{x}+\mathrm{3}{y}=\mathrm{8} \\ $$$$\mathrm{2}{x}+\mathrm{10}{y}=\mathrm{22} \\ $$$${so}\:\mathrm{7}{y}=\mathrm{14} \\ $$$${y}=\mathrm{2} \\ $$$${x}+\mathrm{10}−\mathrm{11}=\mathrm{0} \\ $$$${x}=\mathrm{1} \\ $$

Answered by Rio Mike last updated on 27/May/18

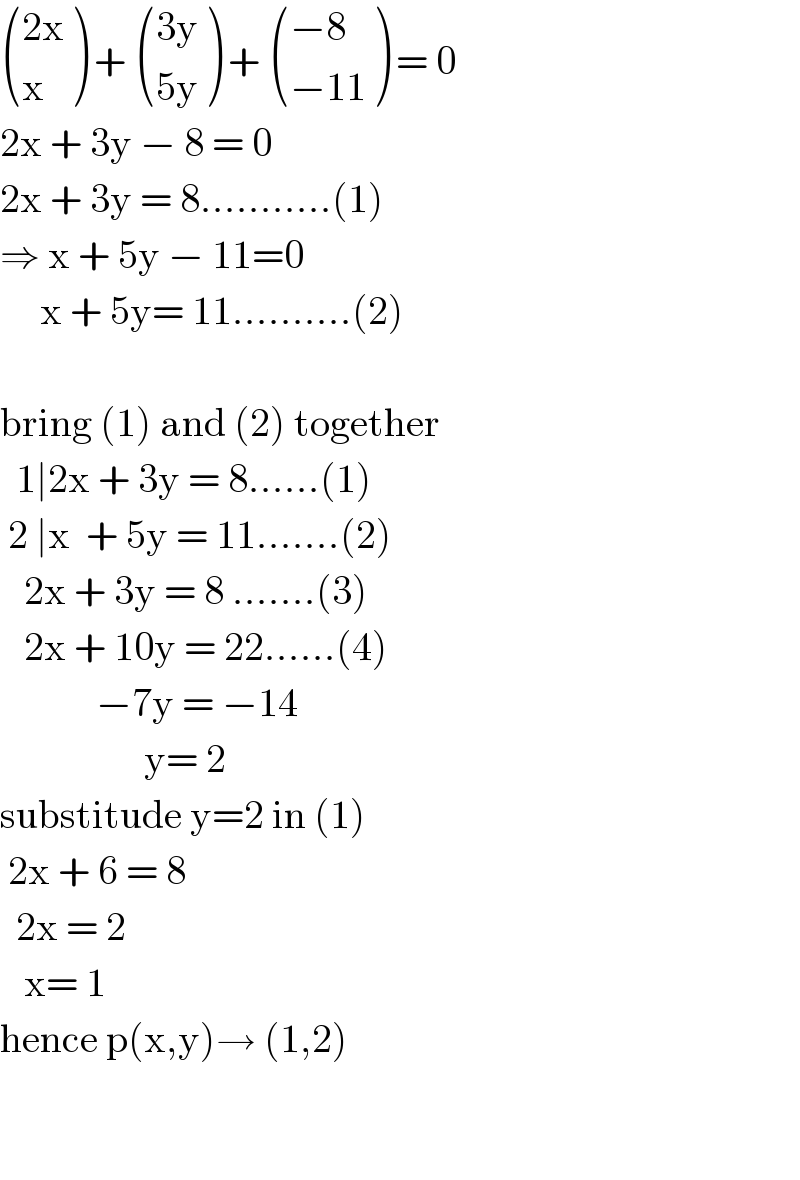
$$\begin{pmatrix}{\mathrm{2x}}\\{\mathrm{x}}\end{pmatrix}\:+\:\begin{pmatrix}{\mathrm{3y}}\\{\mathrm{5y}}\end{pmatrix}\:+\:\begin{pmatrix}{−\mathrm{8}}\\{−\mathrm{11}}\end{pmatrix}\:=\:\mathrm{0} \\ $$$$\mathrm{2x}\:+\:\mathrm{3y}\:−\:\mathrm{8}\:=\:\mathrm{0} \\ $$$$\mathrm{2x}\:+\:\mathrm{3y}\:=\:\mathrm{8}………..\left(\mathrm{1}\right) \\ $$$$\Rightarrow\:\mathrm{x}\:+\:\mathrm{5y}\:−\:\mathrm{11}=\mathrm{0} \\ $$$$\:\:\:\:\:\mathrm{x}\:+\:\mathrm{5y}=\:\mathrm{11}……….\left(\mathrm{2}\right) \\ $$$$ \\ $$$$\mathrm{bring}\:\left(\mathrm{1}\right)\:\mathrm{and}\:\left(\mathrm{2}\right)\:\mathrm{together}\: \\ $$$$\:\:\mathrm{1}\mid\mathrm{2x}\:+\:\mathrm{3y}\:=\:\mathrm{8}……\left(\mathrm{1}\right) \\ $$$$\:\mathrm{2}\:\mid\mathrm{x}\:\:+\:\mathrm{5y}\:=\:\mathrm{11}…….\left(\mathrm{2}\right) \\ $$$$\:\:\:\mathrm{2x}\:+\:\mathrm{3y}\:=\:\mathrm{8}\:…….\left(\mathrm{3}\right) \\ $$$$\:\:\:\mathrm{2x}\:+\:\mathrm{10y}\:=\:\mathrm{22}……\left(\mathrm{4}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:−\mathrm{7y}\:=\:−\mathrm{14} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{y}=\:\mathrm{2} \\ $$$$\mathrm{substitude}\:\mathrm{y}=\mathrm{2}\:\mathrm{in}\:\left(\mathrm{1}\right)\: \\ $$$$\:\mathrm{2x}\:+\:\mathrm{6}\:=\:\mathrm{8} \\ $$$$\:\:\mathrm{2x}\:=\:\mathrm{2}\: \\ $$$$\:\:\:\mathrm{x}=\:\mathrm{1} \\ $$$$\mathrm{hence}\:\mathrm{p}\left(\mathrm{x},\mathrm{y}\right)\rightarrow\:\left(\mathrm{1},\mathrm{2}\right) \\ $$$$ \\ $$$$ \\ $$

Terms of Service
Privacy Policy
Contact: info@tinkutara.com