Question Number 91558 by jagoll last updated on 01/May/20
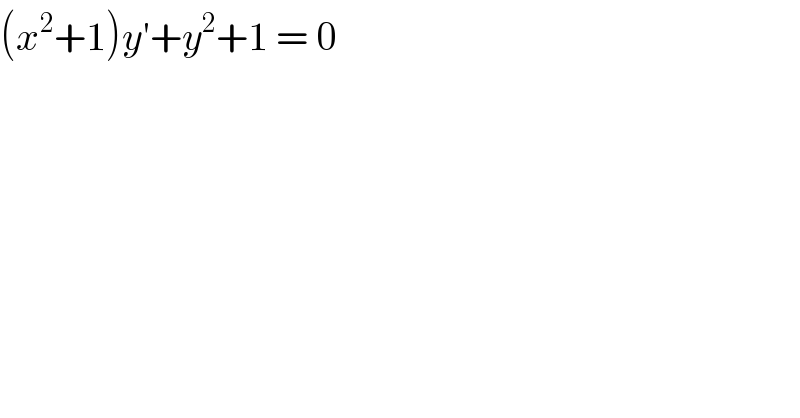
$$\left({x}^{\mathrm{2}} +\mathrm{1}\right){y}'+{y}^{\mathrm{2}} +\mathrm{1}\:=\:\mathrm{0}\: \\ $$
Commented by jagoll last updated on 01/May/20
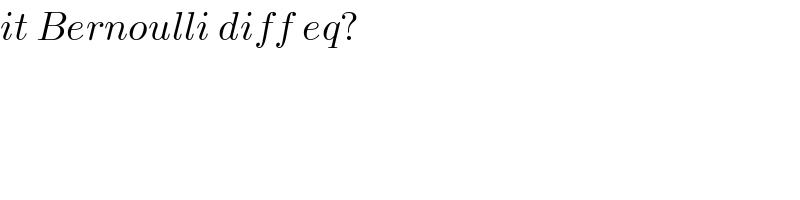
$${it}\:{Bernoulli}\:{diff}\:{eq}? \\ $$
Answered by niroj last updated on 01/May/20

$$\:\:\mathrm{I}\:\mathrm{think}\:\mathrm{its}\:\mathrm{not}\:\mathrm{be}\:\mathrm{a}\:\mathrm{Bernoulli}'\mathrm{s}\:\mathrm{equation}.\:\mathrm{It}\:\mathrm{might}\:\mathrm{be}\: \\ $$$$\:\mathrm{First}\:\mathrm{order}\:\mathrm{Veriables}\:\mathrm{Separable}\:\:\mathrm{Differential}\:\mathrm{Equation}.\: \\ $$$$\:\:\left(\mathrm{x}^{\mathrm{2}} +\mathrm{1}\right)\mathrm{y}^{'} +\mathrm{y}^{\mathrm{2}} +\mathrm{1}=\mathrm{0} \\ $$$$\:\:\left(\mathrm{x}^{\mathrm{2}} +\mathrm{1}\right)\frac{\mathrm{dy}}{\mathrm{dx}}+\mathrm{y}^{\mathrm{2}} +\mathrm{1}=\mathrm{0} \\ $$$$\:\:\left(\mathrm{x}^{\mathrm{2}} +\mathrm{1}\right)\frac{\mathrm{dy}}{\mathrm{dx}}=\:−\left(\mathrm{y}^{\mathrm{2}} +\mathrm{1}\right) \\ $$$$\:\:\:\:\frac{\mathrm{1}}{\mathrm{y}^{\mathrm{2}} +\mathrm{1}}\mathrm{dy}=−\:\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} +\mathrm{1}}\mathrm{dx} \\ $$$$\:\:\:\mathrm{On}\:\mathrm{Integrating}\:\mathrm{both}\:\mathrm{side}, \\ $$$$\:\:\int\:\frac{\mathrm{1}}{\mathrm{y}^{\mathrm{2}} +\mathrm{1}}\mathrm{dy}\:=−\:\int\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} +\mathrm{1}}\mathrm{dx} \\ $$$$\:\:\mathrm{tan}^{−\mathrm{1}} \mathrm{y}\:=−\:\mathrm{tan}^{−\mathrm{1}} \mathrm{x}\:+\mathrm{C} \\ $$$$\:\mathrm{tan}^{−\mathrm{1}} \mathrm{x}+\:\mathrm{tan}^{−\mathrm{1}} \mathrm{y}\:=\:\mathrm{C}\://. \\ $$
Commented by jagoll last updated on 01/May/20

$${yes}.\:{agree} \\ $$
Answered by jagoll last updated on 01/May/20
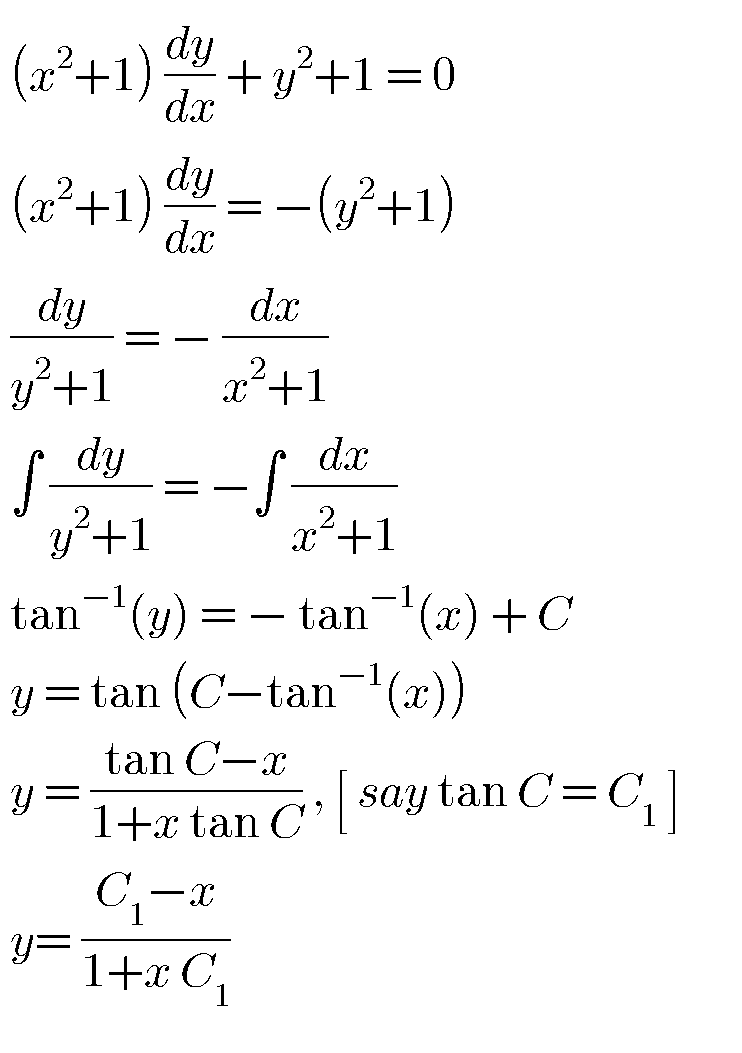
Commented by niroj last updated on 01/May/20
����
