Question Number 131058 by pipin last updated on 01/Feb/21

$$\int\frac{\left(\mathrm{x}^{\mathrm{2}} +\mathrm{2}\right)\left(\mathrm{x}^{\mathrm{2}} +\mathrm{3}\right)\left(\mathrm{x}^{\mathrm{2}} +\mathrm{4}\right)}{\left(\mathrm{x}^{\mathrm{2}} +\mathrm{5}\right)\left(\mathrm{x}^{\mathrm{2}} +\mathrm{6}\right)\left(\mathrm{x}^{\mathrm{2}} +\mathrm{7}\right)}\:\mathrm{dx}\: \\ $$
Answered by MJS_new last updated on 01/Feb/21
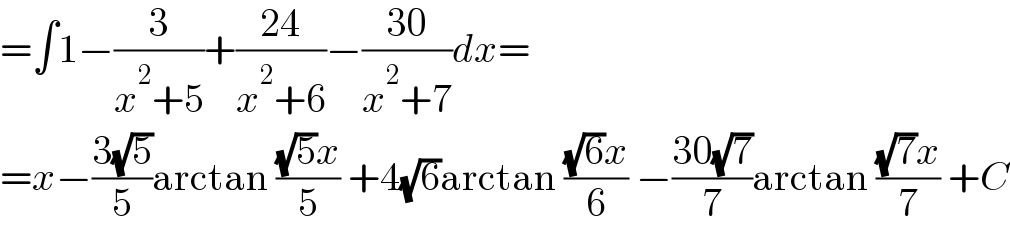
$$=\int\mathrm{1}−\frac{\mathrm{3}}{{x}^{\mathrm{2}} +\mathrm{5}}+\frac{\mathrm{24}}{{x}^{\mathrm{2}} +\mathrm{6}}−\frac{\mathrm{30}}{{x}^{\mathrm{2}} +\mathrm{7}}{dx}= \\ $$$$={x}−\frac{\mathrm{3}\sqrt{\mathrm{5}}}{\mathrm{5}}\mathrm{arctan}\:\frac{\sqrt{\mathrm{5}}{x}}{\mathrm{5}}\:+\mathrm{4}\sqrt{\mathrm{6}}\mathrm{arctan}\:\frac{\sqrt{\mathrm{6}}{x}}{\mathrm{6}}\:−\frac{\mathrm{30}\sqrt{\mathrm{7}}}{\mathrm{7}}\mathrm{arctan}\:\frac{\sqrt{\mathrm{7}}{x}}{\mathrm{7}}\:+{C} \\ $$
