Question Number 162088 by mathlove last updated on 26/Dec/21
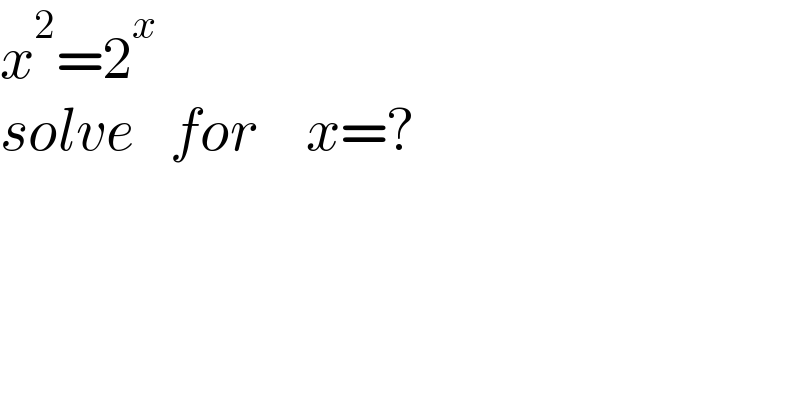
$${x}^{\mathrm{2}} =\mathrm{2}^{{x}} \\ $$$${solve}\:\:\:{for}\:\:\:\:{x}=? \\ $$
Answered by Ar Brandon last updated on 26/Dec/21
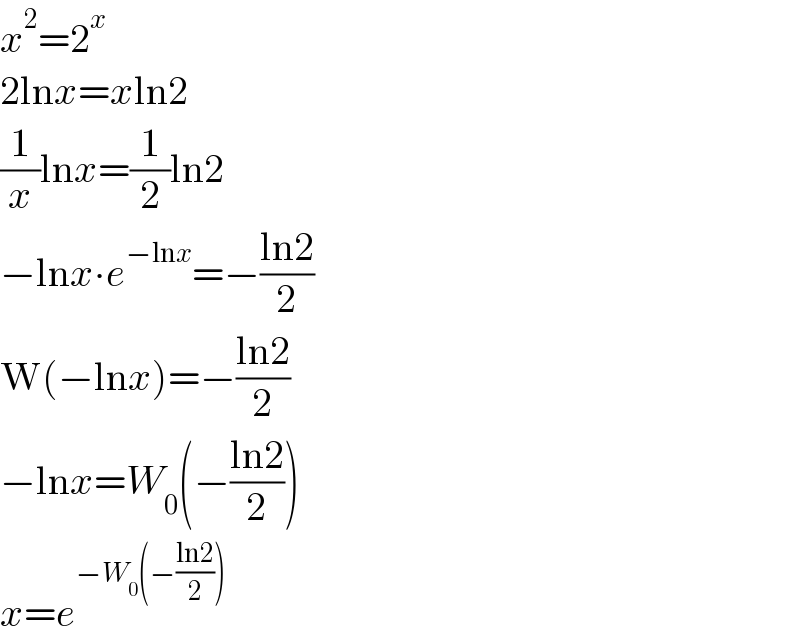
$${x}^{\mathrm{2}} =\mathrm{2}^{{x}} \\ $$$$\mathrm{2ln}{x}={x}\mathrm{ln2} \\ $$$$\frac{\mathrm{1}}{{x}}\mathrm{ln}{x}=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln2} \\ $$$$−\mathrm{ln}{x}\centerdot{e}^{−\mathrm{ln}{x}} =−\frac{\mathrm{ln2}}{\mathrm{2}} \\ $$$$\mathrm{W}\left(−\mathrm{ln}{x}\right)=−\frac{\mathrm{ln2}}{\mathrm{2}} \\ $$$$−\mathrm{ln}{x}={W}_{\mathrm{0}} \left(−\frac{\mathrm{ln2}}{\mathrm{2}}\right) \\ $$$${x}={e}^{−{W}_{\mathrm{0}} \left(−\frac{\mathrm{ln2}}{\mathrm{2}}\right)} \\ $$
Commented by mathlove last updated on 26/Dec/21

$$ \\ $$The numerical answer is
Commented by mr W last updated on 26/Dec/21
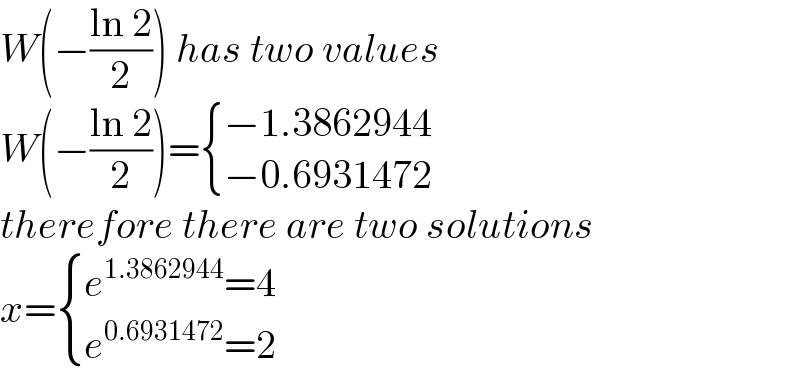
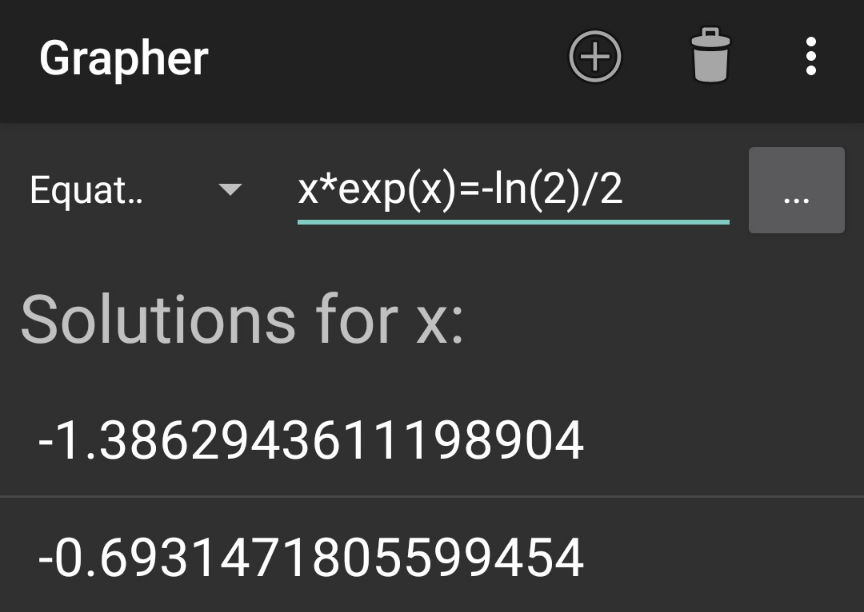
$${W}\left(−\frac{\mathrm{ln}\:\mathrm{2}}{\mathrm{2}}\right)\:{has}\:{two}\:{values} \\ $$$${W}\left(−\frac{\mathrm{ln}\:\mathrm{2}}{\mathrm{2}}\right)=\begin{cases}{−\mathrm{1}.\mathrm{3862944}}\\{−\mathrm{0}.\mathrm{6931472}}\end{cases} \\ $$$${therefore}\:{there}\:{are}\:{two}\:{solutions} \\ $$$${x}=\begin{cases}{{e}^{\mathrm{1}.\mathrm{3862944}} =\mathrm{4}}\\{{e}^{\mathrm{0}.\mathrm{6931472}} =\mathrm{2}}\end{cases} \\ $$
Commented by Ar Brandon last updated on 26/Dec/21

$$\mathrm{Thank}\:\mathrm{you},\:\mathrm{Sir}. \\ $$
Commented by Ar Brandon last updated on 26/Dec/21
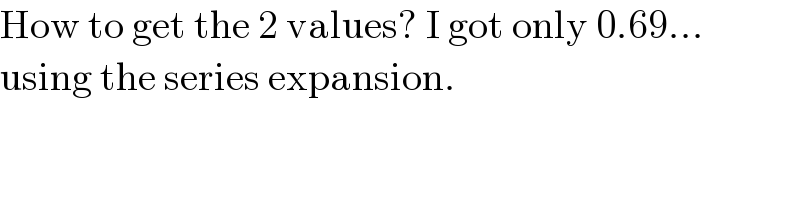
$$\mathrm{How}\:\mathrm{to}\:\mathrm{get}\:\mathrm{the}\:\mathrm{2}\:\mathrm{values}?\:\mathrm{I}\:\mathrm{got}\:\mathrm{only}\:\mathrm{0}.\mathrm{69}… \\ $$$$\mathrm{using}\:\mathrm{the}\:\mathrm{series}\:\mathrm{expansion}. \\ $$
Commented by mr W last updated on 27/Dec/21

$${W}\left(−\frac{\mathrm{ln}\:\mathrm{2}}{\mathrm{2}}\right)\:{is}\:{the}\:{root}\left({s}\right)\:{of} \\ $$$${xe}^{{x}} =−\frac{\mathrm{ln}\:\mathrm{2}}{\mathrm{2}} \\ $$$${there}\:{are}\:{two}\:{roots}.\:{i}\:{got}\:{the} \\ $$$${numeric}\:{values}\:{using}\:{Grapher}: \\ $$
Commented by mathlove last updated on 27/Dec/21

$${thanks}\:\:\:{sir} \\ $$
Commented by mr W last updated on 27/Dec/21
Answered by Rasheed.Sindhi last updated on 27/Dec/21
$${Comparing}\:{exponents}\:{on}\:{both}\:{sides} \\ $$$${and}\:{comparing}\:{bases}\:{on}\:{both}\:{sides} \\ $$$${it}'{s}\:{obvious}\:{that}\:{x}=\mathrm{2}. \\ $$$$\:{x}\leftrightarrows\mathrm{2} \\ $$$${So}\:{x}=\mathrm{2} \\ $$
Commented by mr W last updated on 26/Dec/21

$$\mathrm{2}^{\mathrm{2}} =\mathrm{2}^{\mathrm{2}} \:\Rightarrow{x}=\mathrm{2} \\ $$$${and} \\ $$$$\mathrm{4}^{\mathrm{2}} =\mathrm{2}^{\mathrm{4}} \:\Rightarrow{x}=\mathrm{4} \\ $$
