Question Number 80733 by key of knowledge last updated on 05/Feb/20
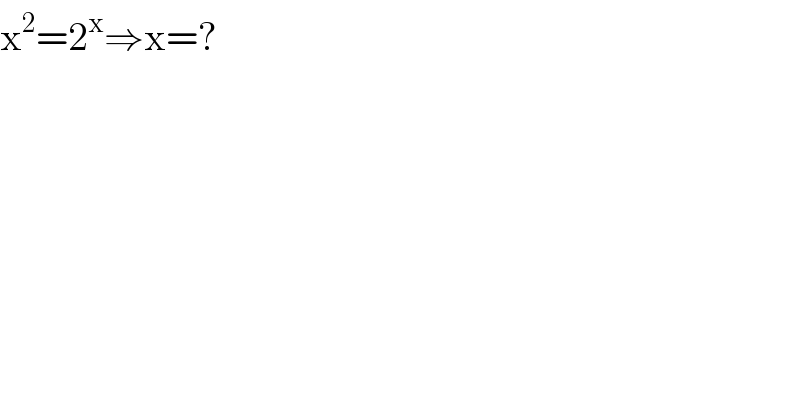
$$\mathrm{x}^{\mathrm{2}} =\mathrm{2}^{\mathrm{x}} \Rightarrow\mathrm{x}=? \\ $$
Commented by mr W last updated on 05/Feb/20
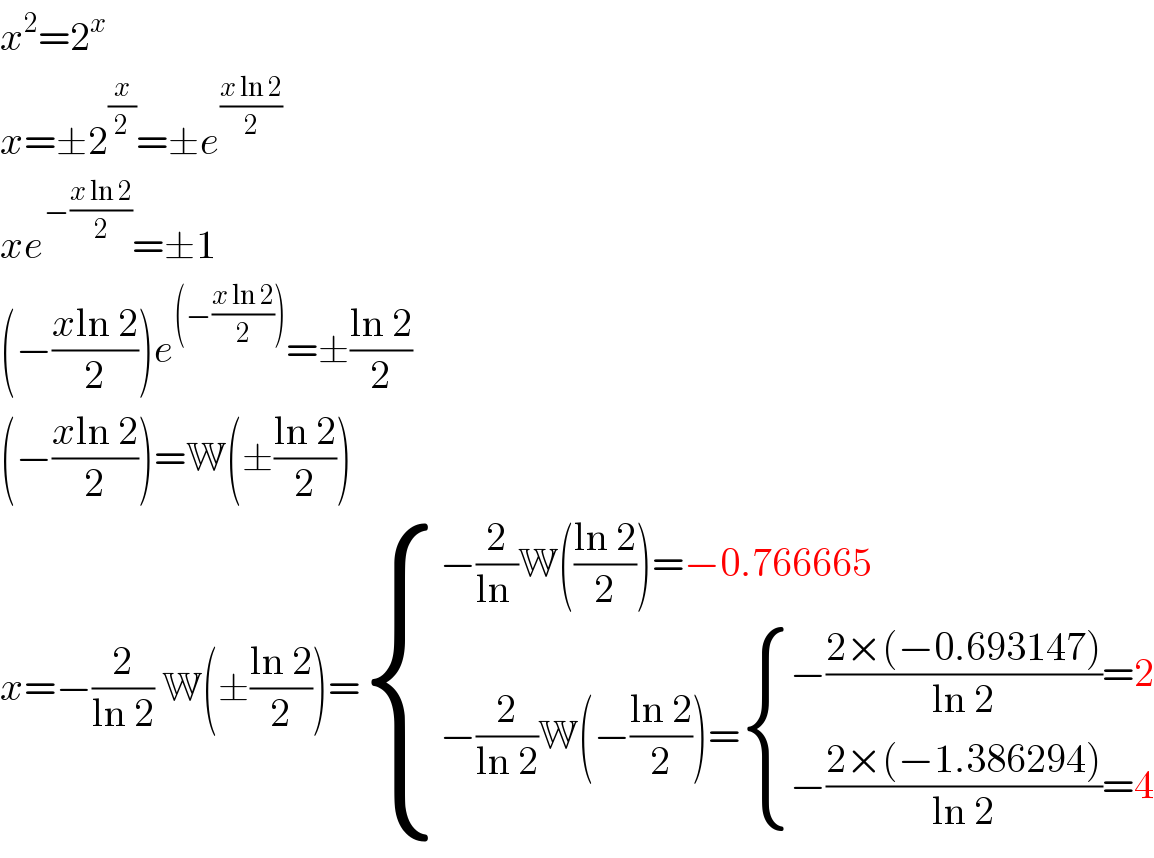
$${x}^{\mathrm{2}} =\mathrm{2}^{{x}} \\ $$$${x}=\pm\mathrm{2}^{\frac{{x}}{\mathrm{2}}} =\pm{e}^{\frac{{x}\:\mathrm{ln}\:\mathrm{2}}{\mathrm{2}}} \\ $$$${xe}^{−\frac{{x}\:\mathrm{ln}\:\mathrm{2}}{\mathrm{2}}} =\pm\mathrm{1} \\ $$$$\left(−\frac{{x}\mathrm{ln}\:\mathrm{2}}{\mathrm{2}}\right){e}^{\left(−\frac{{x}\:\mathrm{ln}\:\mathrm{2}}{\mathrm{2}}\right)} =\pm\frac{\mathrm{ln}\:\mathrm{2}}{\mathrm{2}} \\ $$$$\left(−\frac{{x}\mathrm{ln}\:\mathrm{2}}{\mathrm{2}}\right)=\mathbb{W}\left(\pm\frac{\mathrm{ln}\:\mathrm{2}}{\mathrm{2}}\right) \\ $$$${x}=−\frac{\mathrm{2}}{\mathrm{ln}\:\mathrm{2}}\:\mathbb{W}\left(\pm\frac{\mathrm{ln}\:\mathrm{2}}{\mathrm{2}}\right)=\begin{cases}{−\frac{\mathrm{2}}{\mathrm{ln}\:}\mathbb{W}\left(\frac{\mathrm{ln}\:\mathrm{2}}{\mathrm{2}}\right)=−\mathrm{0}.\mathrm{766665}}\\{−\frac{\mathrm{2}}{\mathrm{ln}\:\mathrm{2}}\mathbb{W}\left(−\frac{\mathrm{ln}\:\mathrm{2}}{\mathrm{2}}\right)=\begin{cases}{−\frac{\mathrm{2}×\left(−\mathrm{0}.\mathrm{693147}\right)}{\mathrm{ln}\:\mathrm{2}}=\mathrm{2}}\\{−\frac{\mathrm{2}×\left(−\mathrm{1}.\mathrm{386294}\right)}{\mathrm{ln}\:\mathrm{2}}=\mathrm{4}}\end{cases}}\end{cases} \\ $$
Commented by key of knowledge last updated on 06/Feb/20
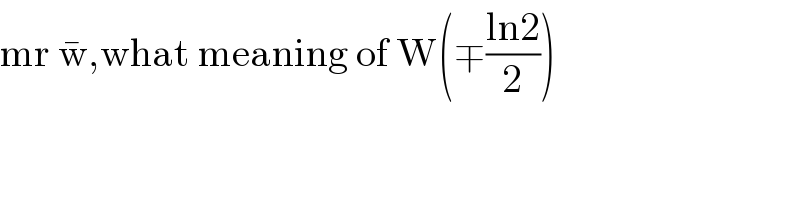
$$\mathrm{mr}\:\bar {\mathrm{w}},\mathrm{what}\:\mathrm{meaning}\:\mathrm{of}\:\mathrm{W}\left(\mp\frac{\mathrm{ln2}}{\mathrm{2}}\right) \\ $$
Commented by mr W last updated on 06/Feb/20
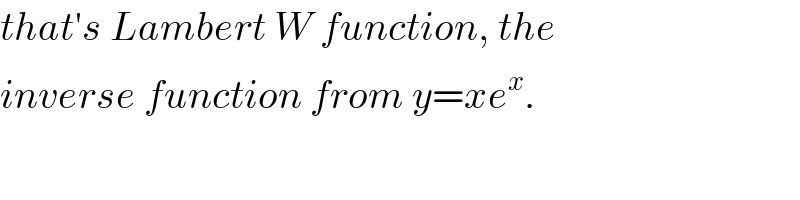
$${that}'{s}\:{Lambert}\:{W}\:{function},\:{the} \\ $$$${inverse}\:{function}\:{from}\:{y}={xe}^{{x}} . \\ $$
