Question Number 44783 by Necxx last updated on 04/Oct/18
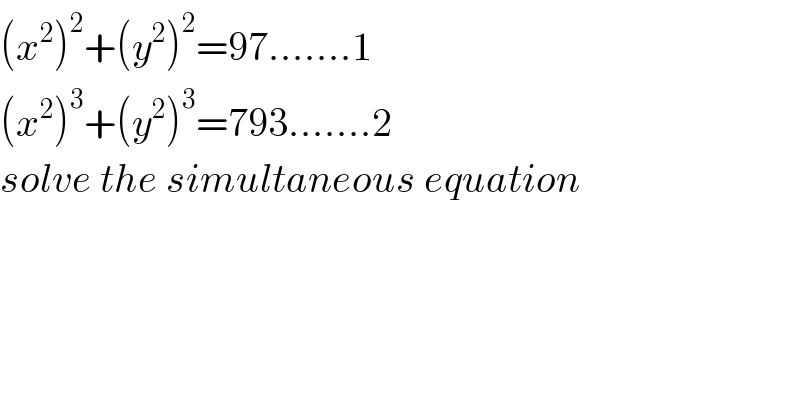
$$\left({x}^{\mathrm{2}} \right)^{\mathrm{2}} +\left({y}^{\mathrm{2}} \right)^{\mathrm{2}} =\mathrm{97}…….\mathrm{1} \\ $$$$\left({x}^{\mathrm{2}} \right)^{\mathrm{3}} +\left({y}^{\mathrm{2}} \right)^{\mathrm{3}} =\mathrm{793}…….\mathrm{2} \\ $$$${solve}\:{the}\:{simultaneous}\:{equation} \\ $$
Answered by ajfour last updated on 05/Oct/18

$${a}^{\mathrm{2}} +{b}^{\mathrm{2}} \:=\:\mathrm{97} \\ $$$${a}^{\mathrm{3}} +{b}^{\mathrm{3}} =\:\mathrm{793} \\ $$$$ \\ $$$$\Rightarrow\:\:\left({a}+{b}\right)^{\mathrm{2}} −\mathrm{2}{ab}\:=\:\mathrm{97}\: \\ $$$$\:\&\:\:\:\:\left({a}+{b}\right)^{\mathrm{3}} −\mathrm{3}{ab}\left({a}+{b}\right)=\mathrm{793} \\ $$$${let}\:\:{a}+{b}\:=\:{r}\:\:\:\:\&\:\:{ab}\:=\:{s} \\ $$$$\Rightarrow\:\:\:{r}^{\mathrm{2}} −\mathrm{2}{s}\:=\:\mathrm{97}\:\:\:\& \\ $$$$\:\:\:\:\:\:\:\:{r}^{\mathrm{3}} −\mathrm{3}{rs}\:=\:\mathrm{793} \\ $$$$\Rightarrow\:\:\:\mathrm{2}{r}^{\mathrm{3}} −\mathrm{3}{r}\left({r}^{\mathrm{3}} −\mathrm{97}\right)=\mathrm{1586} \\ $$$$\Rightarrow\:\:\:{r}^{\mathrm{3}} −\mathrm{291}{r}\:+\mathrm{1586}\:=\:\mathrm{0} \\ $$$${solution}\:{of}\:{a}\:{cubic}\:{of}\:{the}\:{form} \\ $$$$\:\:\:\:{x}^{\mathrm{3}} +{px}+{q}\:=\:\mathrm{0}\:\:\:{is} \\ $$$$\:\boldsymbol{{x}}=\:\left(−\frac{\boldsymbol{{q}}}{\mathrm{2}}+\sqrt{\frac{\boldsymbol{{q}}^{\mathrm{2}} }{\mathrm{4}}+\frac{\boldsymbol{{p}}^{\mathrm{3}} }{\mathrm{27}}}\:\right)^{\mathrm{1}/\mathrm{3}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:−\left(\frac{\boldsymbol{{q}}}{\mathrm{2}}+\sqrt{\frac{\boldsymbol{{q}}^{\mathrm{2}} }{\mathrm{4}}+\frac{\boldsymbol{{p}}^{\mathrm{3}} }{\mathrm{27}}}\:\right)^{\mathrm{1}/\mathrm{3}} \\ $$$$\left({if}\:{it}\:{has}\:{one}\:{real}\:{root}\right) \\ $$$${Here}\:{we}\:{have} \\ $$$$\:\:\:\:\:\:\:\boldsymbol{{r}}^{\mathrm{3}} −\mathrm{291}\boldsymbol{{r}}+\mathrm{1586}\:=\:\mathrm{0} \\ $$$$\:\:{calculator}\:{provides}\:{the}\:{real}\:{root}, \\ $$$$\:\:\:\boldsymbol{{r}}\:=\:\mathrm{13}\:,\:\boldsymbol{{s}}\:=\:\frac{{r}^{\mathrm{2}} −\mathrm{97}}{\mathrm{2}}\:=\:\frac{\mathrm{169}−\mathrm{97}}{\mathrm{2}} \\ $$$$\Rightarrow\:\:\boldsymbol{{s}}\:=\:\mathrm{36} \\ $$$$\Rightarrow\:\:{a}+{b}\:=\:\mathrm{13},\:\:{ab}\:=\:\mathrm{36} \\ $$$${x}=\:\pm\mathrm{9},\:\:{y}\:=\:\pm\mathrm{4}\:\:{or} \\ $$$${x}=\:\pm\mathrm{4},\:\:{y}=\:\pm\mathrm{9}\:. \\ $$
Commented by Necxx last updated on 05/Oct/18
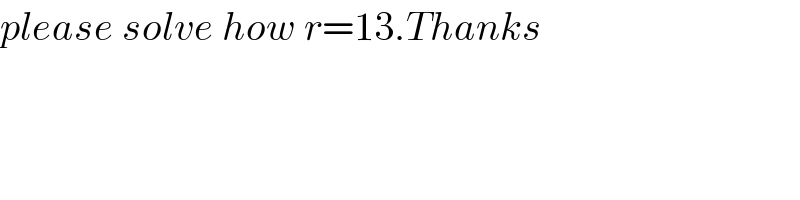
$${please}\:{solve}\:{how}\:{r}=\mathrm{13}.{Thanks} \\ $$
Commented by Necxx last updated on 05/Oct/18
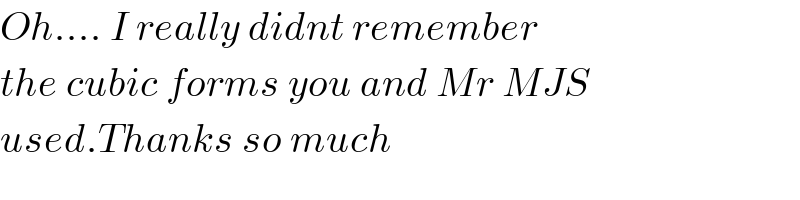
$${Oh}….\:{I}\:{really}\:{didnt}\:{remember} \\ $$$${the}\:{cubic}\:{forms}\:{you}\:{and}\:{Mr}\:{MJS} \\ $$$${used}.{Thanks}\:{so}\:{much} \\ $$
