Question Number 83923 by jagoll last updated on 08/Mar/20
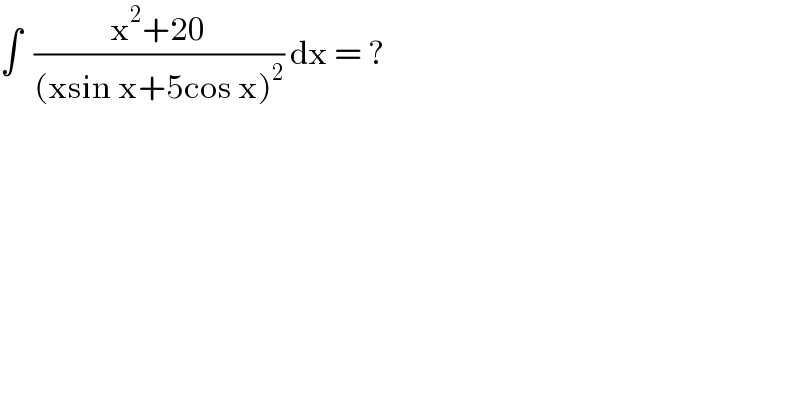
$$\int\:\:\frac{\mathrm{x}^{\mathrm{2}} +\mathrm{20}}{\left(\mathrm{xsin}\:\mathrm{x}+\mathrm{5cos}\:\mathrm{x}\right)^{\mathrm{2}} }\:\mathrm{dx}\:=\:? \\ $$
Answered by john santu last updated on 08/Mar/20
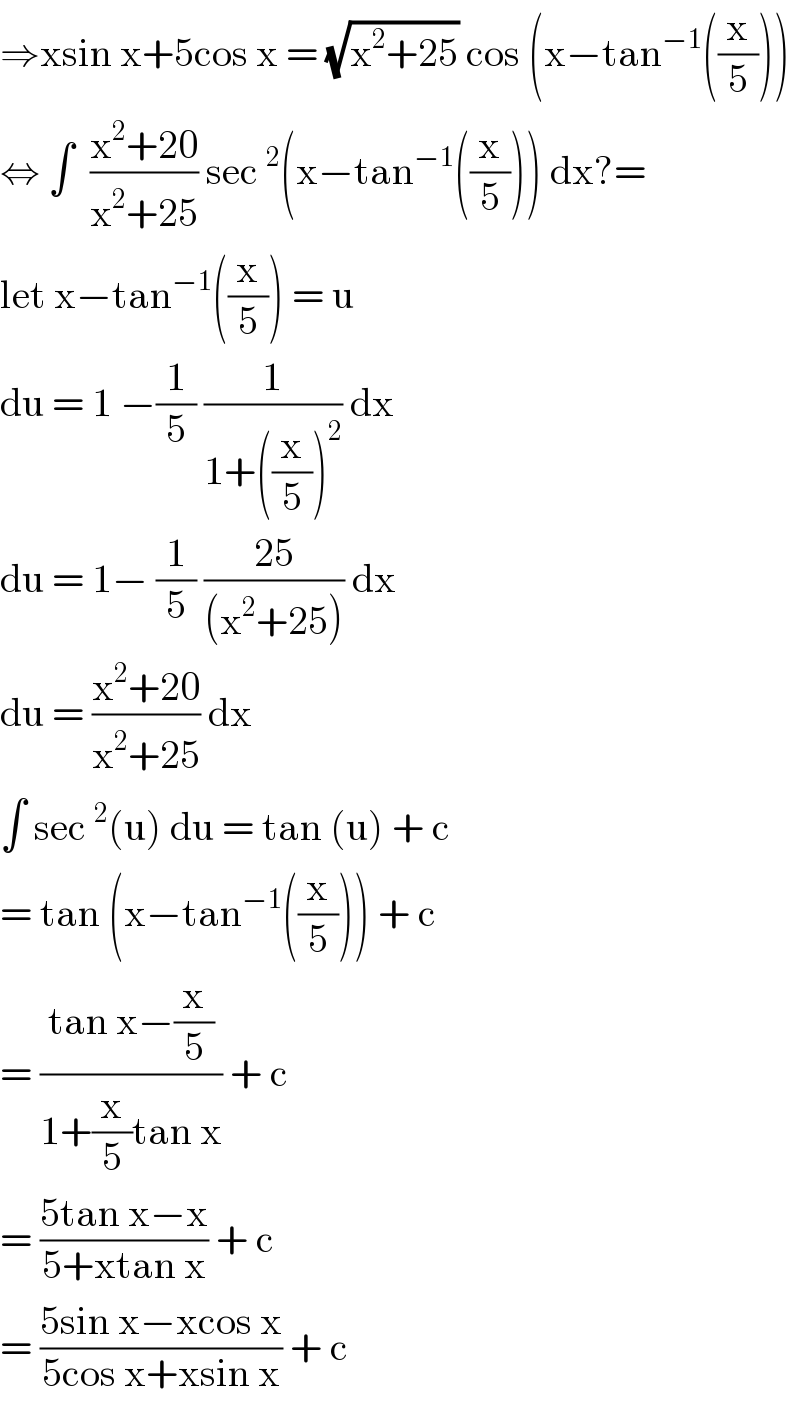
$$\Rightarrow\mathrm{xsin}\:\mathrm{x}+\mathrm{5cos}\:\mathrm{x}\:=\:\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{25}}\:\mathrm{cos}\:\left(\mathrm{x}−\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{x}}{\mathrm{5}}\right)\right) \\ $$$$\Leftrightarrow\:\int\:\:\frac{\mathrm{x}^{\mathrm{2}} +\mathrm{20}}{\mathrm{x}^{\mathrm{2}} +\mathrm{25}}\:\mathrm{sec}\:^{\mathrm{2}} \left(\mathrm{x}−\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{x}}{\mathrm{5}}\right)\right)\:\mathrm{dx}?= \\ $$$$\mathrm{let}\:\mathrm{x}−\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{x}}{\mathrm{5}}\right)\:=\:\mathrm{u}\: \\ $$$$\mathrm{du}\:=\:\mathrm{1}\:−\frac{\mathrm{1}}{\mathrm{5}}\:\frac{\mathrm{1}}{\mathrm{1}+\left(\frac{\mathrm{x}}{\mathrm{5}}\right)^{\mathrm{2}} }\:\mathrm{dx} \\ $$$$\mathrm{du}\:=\:\mathrm{1}−\:\frac{\mathrm{1}}{\mathrm{5}}\:\frac{\mathrm{25}}{\left(\mathrm{x}^{\mathrm{2}} +\mathrm{25}\right)}\:\mathrm{dx} \\ $$$$\mathrm{du}\:=\:\frac{\mathrm{x}^{\mathrm{2}} +\mathrm{20}}{\mathrm{x}^{\mathrm{2}} +\mathrm{25}}\:\mathrm{dx}\: \\ $$$$\int\:\mathrm{sec}\:^{\mathrm{2}} \left(\mathrm{u}\right)\:\mathrm{du}\:=\:\mathrm{tan}\:\left(\mathrm{u}\right)\:+\:\mathrm{c} \\ $$$$=\:\mathrm{tan}\:\left(\mathrm{x}−\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{x}}{\mathrm{5}}\right)\right)\:+\:\mathrm{c} \\ $$$$=\:\frac{\mathrm{tan}\:\mathrm{x}−\frac{\mathrm{x}}{\mathrm{5}}}{\mathrm{1}+\frac{\mathrm{x}}{\mathrm{5}}\mathrm{tan}\:\mathrm{x}}\:+\:\mathrm{c} \\ $$$$=\:\frac{\mathrm{5tan}\:\mathrm{x}−\mathrm{x}}{\mathrm{5}+\mathrm{xtan}\:\mathrm{x}}\:+\:\mathrm{c}\: \\ $$$$=\:\frac{\mathrm{5sin}\:\mathrm{x}−\mathrm{xcos}\:\mathrm{x}}{\mathrm{5cos}\:\mathrm{x}+\mathrm{xsin}\:\mathrm{x}}\:+\:\mathrm{c} \\ $$
Commented by jagoll last updated on 08/Mar/20

$$\mathrm{thank}\:\mathrm{you} \\ $$
