Question Number 96072 by i jagooll last updated on 29/May/20
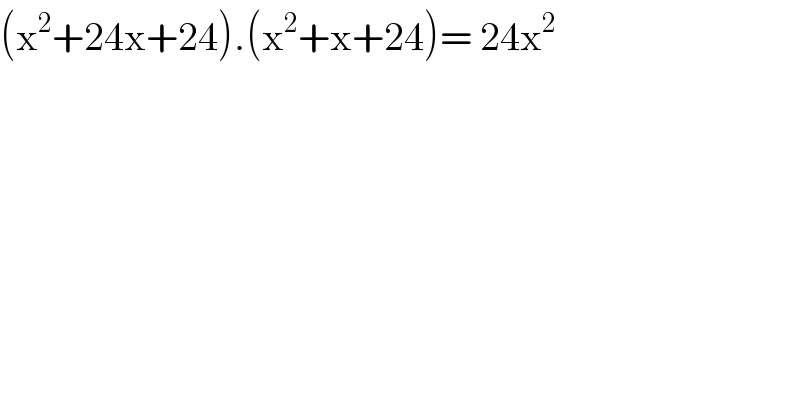
$$\left(\mathrm{x}^{\mathrm{2}} +\mathrm{24x}+\mathrm{24}\right).\left(\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{24}\right)=\:\mathrm{24x}^{\mathrm{2}} \\ $$
Answered by bobhans last updated on 29/May/20
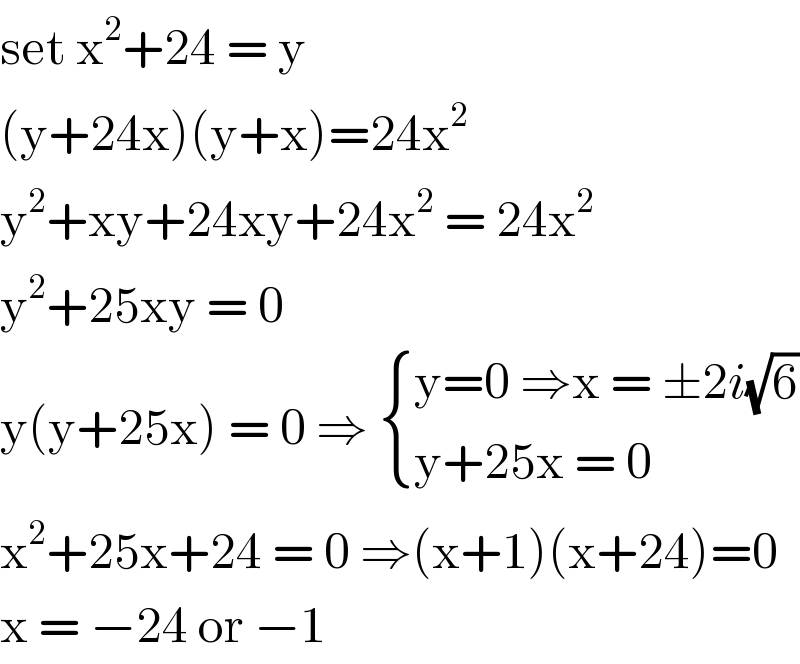
$$\mathrm{set}\:\mathrm{x}^{\mathrm{2}} +\mathrm{24}\:=\:\mathrm{y}\: \\ $$$$\left(\mathrm{y}+\mathrm{24x}\right)\left(\mathrm{y}+\mathrm{x}\right)=\mathrm{24x}^{\mathrm{2}} \\ $$$$\mathrm{y}^{\mathrm{2}} +\mathrm{xy}+\mathrm{24xy}+\mathrm{24x}^{\mathrm{2}} \:=\:\mathrm{24x}^{\mathrm{2}} \: \\ $$$$\mathrm{y}^{\mathrm{2}} +\mathrm{25xy}\:=\:\mathrm{0} \\ $$$$\mathrm{y}\left(\mathrm{y}+\mathrm{25x}\right)\:=\:\mathrm{0}\:\Rightarrow\:\begin{cases}{\mathrm{y}=\mathrm{0}\:\Rightarrow\mathrm{x}\:=\:\pm\mathrm{2}{i}\sqrt{\mathrm{6}}}\\{\mathrm{y}+\mathrm{25x}\:=\:\mathrm{0}\:}\end{cases} \\ $$$$\mathrm{x}^{\mathrm{2}} +\mathrm{25x}+\mathrm{24}\:=\:\mathrm{0}\:\Rightarrow\left(\mathrm{x}+\mathrm{1}\right)\left(\mathrm{x}+\mathrm{24}\right)=\mathrm{0} \\ $$$$\mathrm{x}\:=\:−\mathrm{24}\:\mathrm{or}\:−\mathrm{1}\: \\ $$
Commented by i jagooll last updated on 29/May/20
coooollll ������
