Menu Close

x-2-2x-3-x-2-x-1-dx-

Tinku Tara 0 Comments
Pin




Question Number 88010 by Chi Mes Try last updated on 07/Apr/20
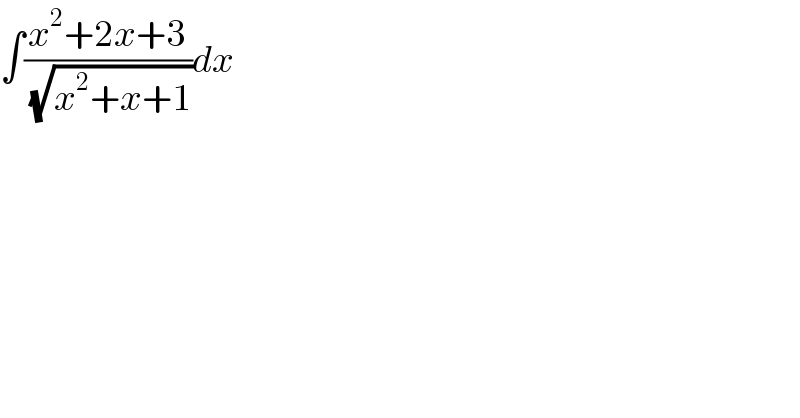
∫((x^2 +2x+3)/( (√(x^2 +x+1))))dx
$$\int\frac{{x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{3}}{\:\sqrt{{x}^{\mathrm{2}} +{x}+\mathrm{1}}}{dx} \\ $$
Commented by niroj last updated on 07/Apr/20
∫((x^2 +2x+3)/( (√(x^2 +x+1))))dx = ∫ ((x^2 +x+1+x+2)/( (√(x^2 +x+1))))dx = ∫ ((x^2 +x+1)/( (√(x^2 +x+1))))dx+ ∫(( x+2)/( (√(x^2 +x+1))))dx = ∫(√(x^2 +x+1)) dx+ ∫ (((1/2)(2x+1)+(3/2))/( (√(x^2 +x+1))))dx = ∫(√(x^2 +2x.(1/2)+(1/4)−(1/4)+))1 dx + (1/2)∫ (((2x+1))/( (√(x^2 +x+1))))dx+(3/2)∫(( 1)/( (√((x+(1/2))^2 +(3/2)))))dx = ∫(√((x+(1/2))^2 +(3/4))) dx +(1/2).2(√(x^2 +x+1))+C+ (3/2)∫ (( 1)/( (√( (x+(1/2))^2 + (((√3)/2))^2 ))))dx = ∫(√((x+(1/2))^2 +(((√3)/2))^2 ))dx + (3/2)∫(1/( (√((x+(1/2))^2 +(((√3)/2))^2 ))))dx +(√(x^2 +x+1)) +C = (((2x+1)(√(x^2 +x+1)))/4)+ (3/8)log (x+(1/2)+(√(x^2 +x+1)) )+ (3/2)log (x+(1/2)+(√(x^2 +x+1)) ) +(√(x^2 +x+1)) +C //.
$$\:\:\:\int\frac{\mathrm{x}^{\mathrm{2}} +\mathrm{2x}+\mathrm{3}}{\:\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}}}\mathrm{dx} \\ $$$$=\:\int\:\frac{\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}+\mathrm{x}+\mathrm{2}}{\:\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}}}\mathrm{dx} \\ $$$$=\:\int\:\frac{\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}}{\:\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}}}\mathrm{dx}+\:\int\frac{\:\mathrm{x}+\mathrm{2}}{\:\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}}}\mathrm{dx} \\ $$$$\:\:\:=\:\int\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}}\:\:\mathrm{dx}+\:\int\:\frac{\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{2x}+\mathrm{1}\right)+\frac{\mathrm{3}}{\mathrm{2}}}{\:\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}}}\mathrm{dx} \\ $$$$\:\:=\:\int\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{2x}.\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{4}}−\frac{\mathrm{1}}{\mathrm{4}}+}\mathrm{1}\:\mathrm{dx}\:+\:\:\frac{\mathrm{1}}{\mathrm{2}}\int\:\frac{\left(\mathrm{2x}+\mathrm{1}\right)}{\:\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}}}\mathrm{dx}+\frac{\mathrm{3}}{\mathrm{2}}\int\frac{\:\mathrm{1}}{\:\sqrt{\left(\mathrm{x}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +\frac{\mathrm{3}}{\mathrm{2}}}}\mathrm{dx} \\ $$$$=\:\int\sqrt{\left(\mathrm{x}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +\frac{\mathrm{3}}{\mathrm{4}}}\:\:\mathrm{dx}\:+\frac{\mathrm{1}}{\mathrm{2}}.\mathrm{2}\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}}+\mathrm{C}+\:\:\frac{\mathrm{3}}{\mathrm{2}}\int\:\frac{\:\:\mathrm{1}}{\:\sqrt{\:\left(\mathrm{x}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +\:\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right)^{\mathrm{2}} }}\mathrm{dx} \\ $$$$\:=\:\int\sqrt{\left(\mathrm{x}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right)^{\mathrm{2}} }\mathrm{dx}\:+\:\frac{\mathrm{3}}{\mathrm{2}}\int\frac{\mathrm{1}}{\:\sqrt{\left(\mathrm{x}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right)^{\mathrm{2}} }}\mathrm{dx}\:+\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}}\:\:+\mathrm{C} \\ $$$$=\:\:\frac{\left(\mathrm{2x}+\mathrm{1}\right)\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}}}{\mathrm{4}}+\:\frac{\mathrm{3}}{\mathrm{8}}\mathrm{log}\:\left(\mathrm{x}+\frac{\mathrm{1}}{\mathrm{2}}+\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}}\:\right)+\:\frac{\mathrm{3}}{\mathrm{2}}\mathrm{log}\:\left(\mathrm{x}+\frac{\mathrm{1}}{\mathrm{2}}+\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}}\:\right)\:+\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}}\:\:+\mathrm{C}\:\://. \\ $$
Commented by mathmax by abdo last updated on 08/Apr/20
A =∫ ((x^2 +2x+3)/( (√(x^2 +x+1))))dx ⇒A =∫ ((x^2 +2)/( (√(x^2 +x+1))))dx +∫ ((2x+1)/( (√(x^2 +x+1))))dx we have ∫ ((2x+1)/( (√(x^2 +x+1))))dx =2(√(x^2 +x+1)) +c_1 ∫ ((x^2 +2)/( (√(x^2 +x+1))))dx =∫ ((x^2 +2)/( (√((x+(1/2))^2 +(3/4)))))dx =_(x+(1/2)=((√3)/2)sh(t)) =∫ (((((√3)/2)sh(t)−(1/2))^2 +2)/(((√3)/2)ch(t)))×((√3)/2)ch(t)dt =(1/4)∫( ((√3)sh(t)−1)^2 +8) dt = 2t +(1/4)∫(3sh^2 t−2(√3)sh(t)+1)dt =2t +(3/8)∫(ch(2t)−1)dt −((√3)/2)ch(t) +(t/4) =(9/4)t +(3/(16))sh(2t)−((3t)/8)−((√3)/3)ch(t)+C_2 =((15)/8) t +(3/8)sh(t)ch(t) −((√3)/3)ch(t) +c_2 =((15)/8)argsh(((2x+1)/( (√3)))) +(3/8)(((2x+1)/( (√3))))(√(1+(((2x+1)/( (√3))))^2 )) −((√3)/3)(√(1+(((2x+1)/( (√3))))^2 )) +C_2 ⇒ A =2(√(x^2 +x+1)) +((15)/8)ln(((2x+1)/( (√3)))+(√(1+(((2x+1)/( (√3))))^2 )) +(3/8)(((2x+1)/( (√3))))(√(1+(((2x+1)/( (√3))))^2 ))−((√3)/3)(√(1+(((2x+1)/( (√3))))^2 )) +C
$${A}\:=\int\:\:\frac{{x}^{\mathrm{2}} \:+\mathrm{2}{x}+\mathrm{3}}{\:\sqrt{{x}^{\mathrm{2}} \:+{x}+\mathrm{1}}}{dx}\:\Rightarrow{A}\:=\int\:\frac{{x}^{\mathrm{2}} \:+\mathrm{2}}{\:\sqrt{{x}^{\mathrm{2}} \:+{x}+\mathrm{1}}}{dx}\:+\int\:\frac{\mathrm{2}{x}+\mathrm{1}}{\:\sqrt{{x}^{\mathrm{2}} \:+{x}+\mathrm{1}}}{dx} \\ $$$${we}\:{have}\:\int\:\frac{\mathrm{2}{x}+\mathrm{1}}{\:\sqrt{{x}^{\mathrm{2}} \:+{x}+\mathrm{1}}}{dx}\:=\mathrm{2}\sqrt{{x}^{\mathrm{2}} \:+{x}+\mathrm{1}}\:+{c}_{\mathrm{1}} \\ $$$$\int\:\frac{{x}^{\mathrm{2}} \:+\mathrm{2}}{\:\sqrt{{x}^{\mathrm{2}} +{x}+\mathrm{1}}}{dx}\:=\int\:\frac{{x}^{\mathrm{2}} \:+\mathrm{2}}{\:\sqrt{\left({x}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} \:+\frac{\mathrm{3}}{\mathrm{4}}}}{dx}\:=_{{x}+\frac{\mathrm{1}}{\mathrm{2}}=\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}{sh}\left({t}\right)} \\ $$$$=\int\:\:\:\frac{\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}{sh}\left({t}\right)−\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} \:+\mathrm{2}}{\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}{ch}\left({t}\right)}×\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}{ch}\left({t}\right){dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\int\left(\:\:\left(\sqrt{\mathrm{3}}{sh}\left({t}\right)−\mathrm{1}\right)^{\mathrm{2}} \:+\mathrm{8}\right)\:{dt}\:=\:\mathrm{2}{t}\:\:+\frac{\mathrm{1}}{\mathrm{4}}\int\left(\mathrm{3}{sh}^{\mathrm{2}} {t}−\mathrm{2}\sqrt{\mathrm{3}}{sh}\left({t}\right)+\mathrm{1}\right){dt} \\ $$$$=\mathrm{2}{t}\:+\frac{\mathrm{3}}{\mathrm{8}}\int\left({ch}\left(\mathrm{2}{t}\right)−\mathrm{1}\right){dt}\:−\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}{ch}\left({t}\right)\:+\frac{{t}}{\mathrm{4}} \\ $$$$=\frac{\mathrm{9}}{\mathrm{4}}{t}\:+\frac{\mathrm{3}}{\mathrm{16}}{sh}\left(\mathrm{2}{t}\right)−\frac{\mathrm{3}{t}}{\mathrm{8}}−\frac{\sqrt{\mathrm{3}}}{\mathrm{3}}{ch}\left({t}\right)+{C}_{\mathrm{2}} \\ $$$$=\frac{\mathrm{15}}{\mathrm{8}}\:{t}\:\:+\frac{\mathrm{3}}{\mathrm{8}}{sh}\left({t}\right){ch}\left({t}\right)\:−\frac{\sqrt{\mathrm{3}}}{\mathrm{3}}{ch}\left({t}\right)\:+{c}_{\mathrm{2}} \\ $$$$=\frac{\mathrm{15}}{\mathrm{8}}{argsh}\left(\frac{\mathrm{2}{x}+\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right)\:+\frac{\mathrm{3}}{\mathrm{8}}\left(\frac{\mathrm{2}{x}+\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right)\sqrt{\mathrm{1}+\left(\frac{\mathrm{2}{x}+\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right)^{\mathrm{2}} }\:−\frac{\sqrt{\mathrm{3}}}{\mathrm{3}}\sqrt{\mathrm{1}+\left(\frac{\mathrm{2}{x}+\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right)^{\mathrm{2}} }\:+{C}_{\mathrm{2}} \\ $$$$\Rightarrow\:{A}\:=\mathrm{2}\sqrt{{x}^{\mathrm{2}} \:+{x}+\mathrm{1}}\:\:+\frac{\mathrm{15}}{\mathrm{8}}{ln}\left(\frac{\mathrm{2}{x}+\mathrm{1}}{\:\sqrt{\mathrm{3}}}+\sqrt{\mathrm{1}+\left(\frac{\mathrm{2}{x}+\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right)^{\mathrm{2}} }\right. \\ $$$$+\frac{\mathrm{3}}{\mathrm{8}}\left(\frac{\mathrm{2}{x}+\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right)\sqrt{\mathrm{1}+\left(\frac{\mathrm{2}{x}+\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right)^{\mathrm{2}} }−\frac{\sqrt{\mathrm{3}}}{\mathrm{3}}\sqrt{\mathrm{1}+\left(\frac{\mathrm{2}{x}+\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right)^{\mathrm{2}} }\:+{C} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *