Question Number 103454 by bemath last updated on 15/Jul/20
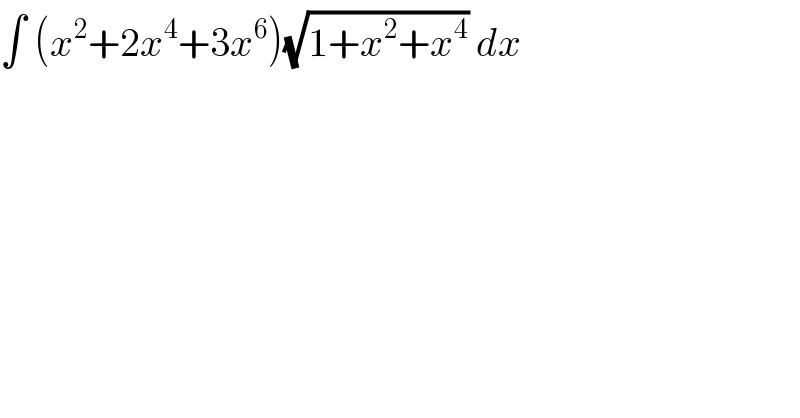
$$\int\:\left({x}^{\mathrm{2}} +\mathrm{2}{x}^{\mathrm{4}} +\mathrm{3}{x}^{\mathrm{6}} \right)\sqrt{\mathrm{1}+{x}^{\mathrm{2}} +{x}^{\mathrm{4}} }\:{dx}\: \\ $$
Answered by bobhans last updated on 15/Jul/20
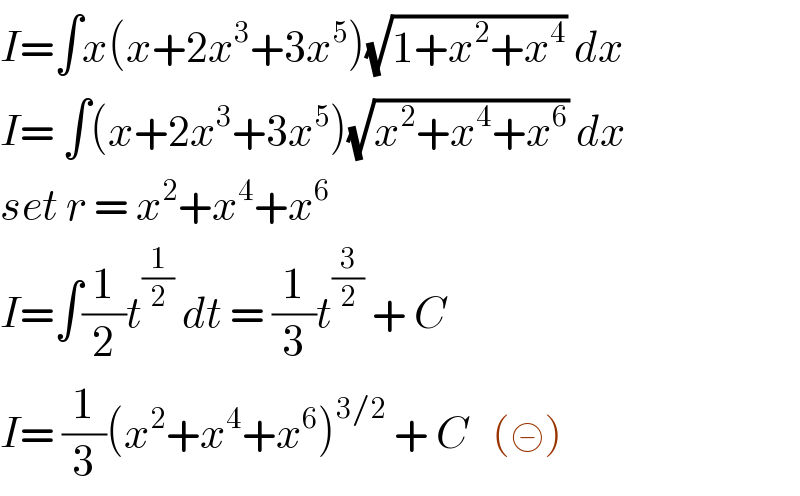
$${I}=\int{x}\left({x}+\mathrm{2}{x}^{\mathrm{3}} +\mathrm{3}{x}^{\mathrm{5}} \right)\sqrt{\mathrm{1}+{x}^{\mathrm{2}} +{x}^{\mathrm{4}} }\:{dx}\: \\ $$$${I}=\:\int\left({x}+\mathrm{2}{x}^{\mathrm{3}} +\mathrm{3}{x}^{\mathrm{5}} \right)\sqrt{{x}^{\mathrm{2}} +{x}^{\mathrm{4}} +{x}^{\mathrm{6}} }\:{dx}\: \\ $$$${set}\:{r}\:=\:{x}^{\mathrm{2}} +{x}^{\mathrm{4}} +{x}^{\mathrm{6}} \: \\ $$$${I}=\int\frac{\mathrm{1}}{\mathrm{2}}{t}^{\frac{\mathrm{1}}{\mathrm{2}}} \:{dt}\:=\:\frac{\mathrm{1}}{\mathrm{3}}{t}^{\frac{\mathrm{3}}{\mathrm{2}}} \:+\:{C} \\ $$$${I}=\:\frac{\mathrm{1}}{\mathrm{3}}\left({x}^{\mathrm{2}} +{x}^{\mathrm{4}} +{x}^{\mathrm{6}} \right)^{\mathrm{3}/\mathrm{2}} \:+\:{C}\:\:\:\left(\circleddash\right)\: \\ $$
