Question Number 103043 by bemath last updated on 12/Jul/20
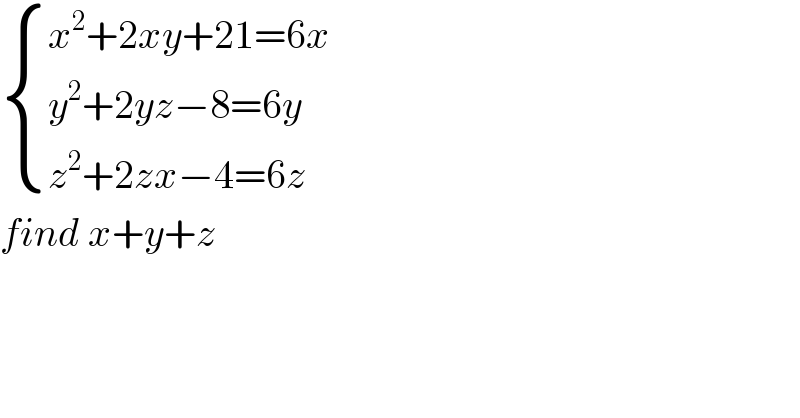
$$\begin{cases}{{x}^{\mathrm{2}} +\mathrm{2}{xy}+\mathrm{21}=\mathrm{6}{x}}\\{{y}^{\mathrm{2}} +\mathrm{2}{yz}−\mathrm{8}=\mathrm{6}{y}}\\{{z}^{\mathrm{2}} +\mathrm{2}{zx}−\mathrm{4}=\mathrm{6}{z}}\end{cases} \\ $$$${find}\:{x}+{y}+{z}\: \\ $$
Answered by maths mind last updated on 12/Jul/20
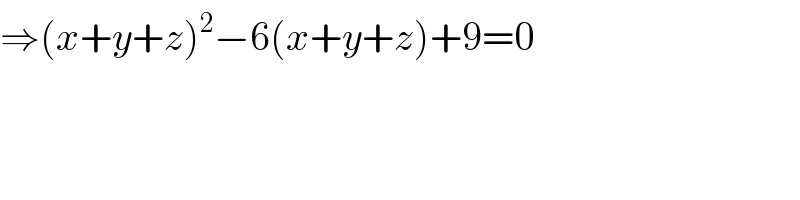
$$\Rightarrow\left({x}+{y}+{z}\right)^{\mathrm{2}} −\mathrm{6}\left({x}+{y}+{z}\right)+\mathrm{9}=\mathrm{0} \\ $$
Commented by bemath last updated on 12/Jul/20
coll ,������
Commented by Rasheed.Sindhi last updated on 12/Jul/20

$$\mathcal{N}{ice}! \\ $$
Answered by Dwaipayan Shikari last updated on 12/Jul/20
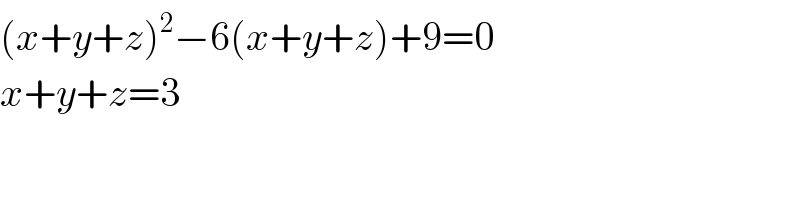
$$\left({x}+{y}+{z}\right)^{\mathrm{2}} −\mathrm{6}\left({x}+{y}+{z}\right)+\mathrm{9}=\mathrm{0} \\ $$$${x}+{y}+{z}=\mathrm{3} \\ $$
