Menu Close

x-2-2y-2-dx-4xy-y-2-dy-0-

Tinku Tara 0 Comments
Pin




Question Number 117029 by bemath last updated on 09/Oct/20
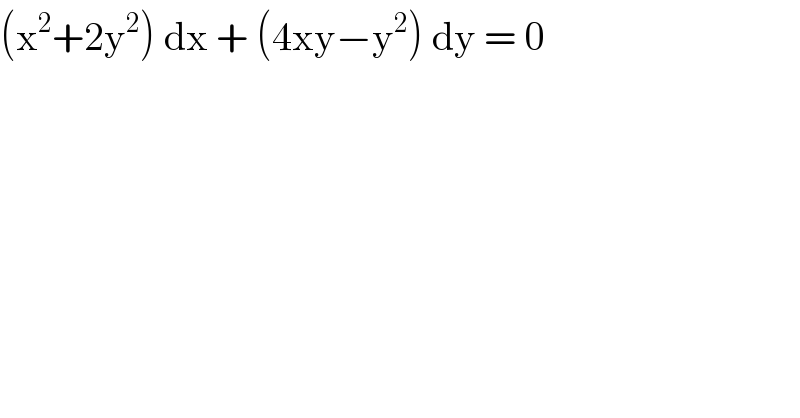
(x^2 +2y^2 ) dx + (4xy−y^2 ) dy = 0
$$\left(\mathrm{x}^{\mathrm{2}} +\mathrm{2y}^{\mathrm{2}} \right)\:\mathrm{dx}\:+\:\left(\mathrm{4xy}−\mathrm{y}^{\mathrm{2}} \right)\:\mathrm{dy}\:=\:\mathrm{0} \\ $$
Answered by bemath last updated on 09/Oct/20
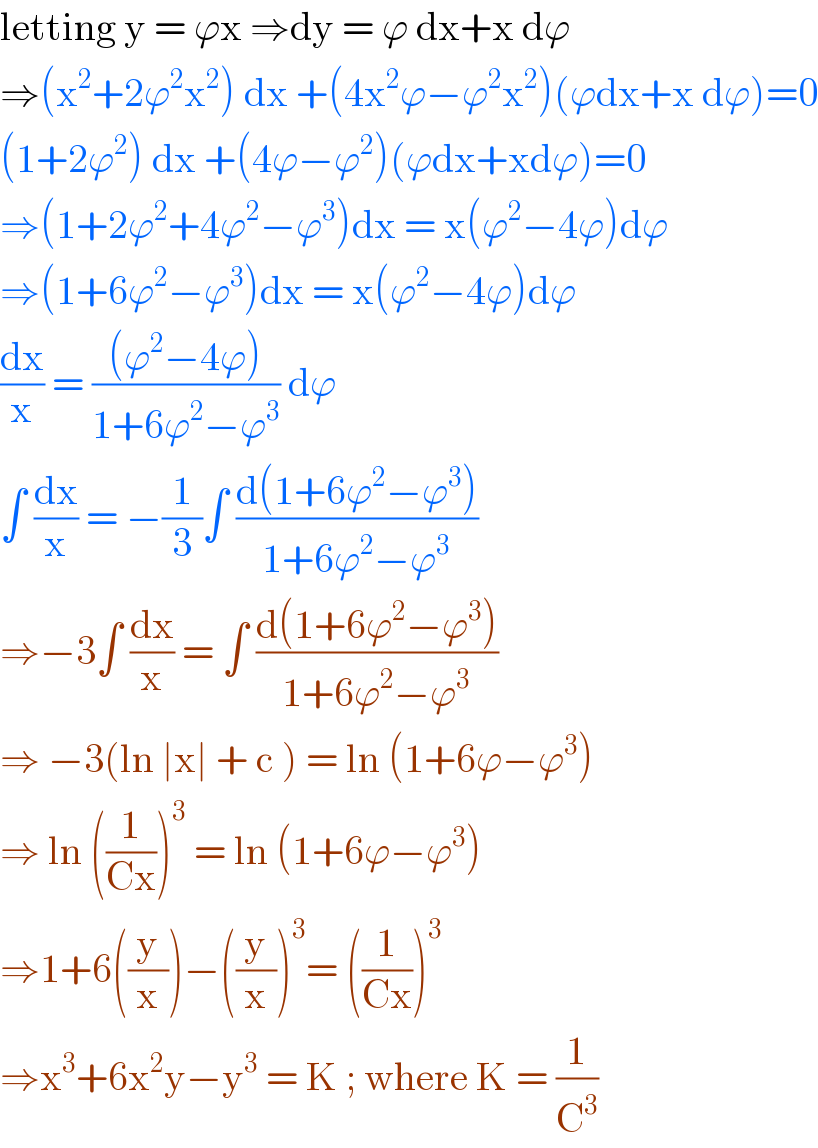
letting y = ϕx ⇒dy = ϕ dx+x dϕ ⇒(x^2 +2ϕ^2 x^2 ) dx +(4x^2 ϕ−ϕ^2 x^2 )(ϕdx+x dϕ)=0 (1+2ϕ^2 ) dx +(4ϕ−ϕ^2 )(ϕdx+xdϕ)=0 ⇒(1+2ϕ^2 +4ϕ^2 −ϕ^3 )dx = x(ϕ^2 −4ϕ)dϕ ⇒(1+6ϕ^2 −ϕ^3 )dx = x(ϕ^2 −4ϕ)dϕ (dx/x) = (((ϕ^2 −4ϕ))/(1+6ϕ^2 −ϕ^3 )) dϕ ∫ (dx/x) = −(1/3)∫ ((d(1+6ϕ^2 −ϕ^3 ))/(1+6ϕ^2 −ϕ^3 )) ⇒−3∫ (dx/x) = ∫ ((d(1+6ϕ^2 −ϕ^3 ))/(1+6ϕ^2 −ϕ^3 )) ⇒ −3(ln ∣x∣ + c ) = ln (1+6ϕ−ϕ^3 ) ⇒ ln ((1/(Cx)))^3 = ln (1+6ϕ−ϕ^3 ) ⇒1+6((y/x))−((y/x))^3 = ((1/(Cx)))^3 ⇒x^3 +6x^2 y−y^3 = K ; where K = (1/C^3 )
$$\mathrm{letting}\:\mathrm{y}\:=\:\varphi\mathrm{x}\:\Rightarrow\mathrm{dy}\:=\:\varphi\:\mathrm{dx}+\mathrm{x}\:\mathrm{d}\varphi \\ $$$$\Rightarrow\left(\mathrm{x}^{\mathrm{2}} +\mathrm{2}\varphi^{\mathrm{2}} \mathrm{x}^{\mathrm{2}} \right)\:\mathrm{dx}\:+\left(\mathrm{4x}^{\mathrm{2}} \varphi−\varphi^{\mathrm{2}} \mathrm{x}^{\mathrm{2}} \right)\left(\varphi\mathrm{dx}+\mathrm{x}\:\mathrm{d}\varphi\right)=\mathrm{0} \\ $$$$\left(\mathrm{1}+\mathrm{2}\varphi^{\mathrm{2}} \right)\:\mathrm{dx}\:+\left(\mathrm{4}\varphi−\varphi^{\mathrm{2}} \right)\left(\varphi\mathrm{dx}+\mathrm{xd}\varphi\right)=\mathrm{0} \\ $$$$\Rightarrow\left(\mathrm{1}+\mathrm{2}\varphi^{\mathrm{2}} +\mathrm{4}\varphi^{\mathrm{2}} −\varphi^{\mathrm{3}} \right)\mathrm{dx}\:=\:\mathrm{x}\left(\varphi^{\mathrm{2}} −\mathrm{4}\varphi\right)\mathrm{d}\varphi \\ $$$$\Rightarrow\left(\mathrm{1}+\mathrm{6}\varphi^{\mathrm{2}} −\varphi^{\mathrm{3}} \right)\mathrm{dx}\:=\:\mathrm{x}\left(\varphi^{\mathrm{2}} −\mathrm{4}\varphi\right)\mathrm{d}\varphi \\ $$$$\frac{\mathrm{dx}}{\mathrm{x}}\:=\:\frac{\left(\varphi^{\mathrm{2}} −\mathrm{4}\varphi\right)}{\mathrm{1}+\mathrm{6}\varphi^{\mathrm{2}} −\varphi^{\mathrm{3}} }\:\mathrm{d}\varphi \\ $$$$\int\:\frac{\mathrm{dx}}{\mathrm{x}}\:=\:−\frac{\mathrm{1}}{\mathrm{3}}\int\:\frac{\mathrm{d}\left(\mathrm{1}+\mathrm{6}\varphi^{\mathrm{2}} −\varphi^{\mathrm{3}} \right)}{\mathrm{1}+\mathrm{6}\varphi^{\mathrm{2}} −\varphi^{\mathrm{3}} } \\ $$$$\Rightarrow−\mathrm{3}\int\:\frac{\mathrm{dx}}{\mathrm{x}}\:=\:\int\:\frac{\mathrm{d}\left(\mathrm{1}+\mathrm{6}\varphi^{\mathrm{2}} −\varphi^{\mathrm{3}} \right)}{\mathrm{1}+\mathrm{6}\varphi^{\mathrm{2}} −\varphi^{\mathrm{3}} } \\ $$$$\Rightarrow\:−\mathrm{3}\left(\mathrm{ln}\:\mid\mathrm{x}\mid\:+\:\mathrm{c}\:\right)\:=\:\mathrm{ln}\:\left(\mathrm{1}+\mathrm{6}\varphi−\varphi^{\mathrm{3}} \right) \\ $$$$\Rightarrow\:\mathrm{ln}\:\left(\frac{\mathrm{1}}{\mathrm{Cx}}\right)^{\mathrm{3}} \:=\:\mathrm{ln}\:\left(\mathrm{1}+\mathrm{6}\varphi−\varphi^{\mathrm{3}} \right) \\ $$$$\Rightarrow\mathrm{1}+\mathrm{6}\left(\frac{\mathrm{y}}{\mathrm{x}}\right)−\left(\frac{\mathrm{y}}{\mathrm{x}}\right)^{\mathrm{3}} =\:\left(\frac{\mathrm{1}}{\mathrm{Cx}}\right)^{\mathrm{3}} \\ $$$$\Rightarrow\mathrm{x}^{\mathrm{3}} +\mathrm{6x}^{\mathrm{2}} \mathrm{y}−\mathrm{y}^{\mathrm{3}} \:=\:\mathrm{K}\:;\:\mathrm{where}\:\mathrm{K}\:=\:\frac{\mathrm{1}}{\mathrm{C}^{\mathrm{3}} } \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *