Menu Close

x-2-2y-2-xy-37-y-2-2x-2-2xy-26-x-2-y-2-

Tinku Tara 0 Comments
Pin




Question Number 146936 by mathdanisur last updated on 16/Jul/21
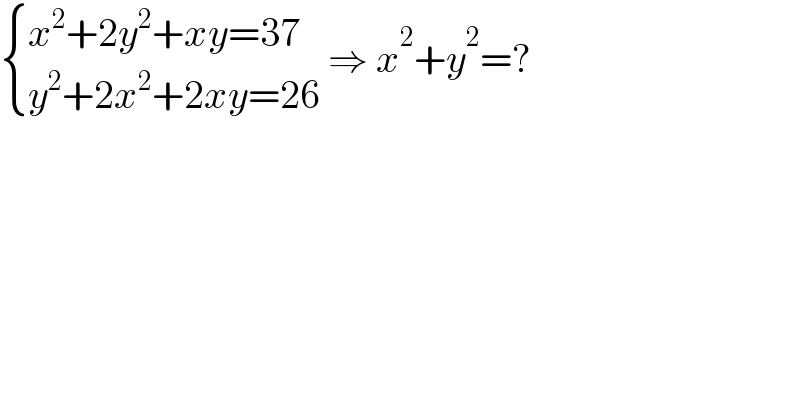
{ ((x^2 +2y^2 +xy=37)),((y^2 +2x^2 +2xy=26)) :} ⇒ x^2 +y^2 =?
$$\begin{cases}{{x}^{\mathrm{2}} +\mathrm{2}{y}^{\mathrm{2}} +{xy}=\mathrm{37}}\\{{y}^{\mathrm{2}} +\mathrm{2}{x}^{\mathrm{2}} +\mathrm{2}{xy}=\mathrm{26}}\end{cases}\:\Rightarrow\:{x}^{\mathrm{2}} +{y}^{\mathrm{2}} =? \\ $$
Answered by TheHoneyCat last updated on 16/Jul/21
let S= { ((x^2 +2y^2 +xy=37)),((y^2 +2x^2 +2xy=26)) :} ⇔ { ((x^2 +2y^2 +xy=37)),((−3y^2 =26−2×37)) :} ⇔ { ((x^2 +2y^2 +xy=37)),((y^2 =16)) :} ⇔ { ((x^2 +32+xy=37)),((y^2 =16)) :} ⇔ { ((x^2 +xy−5=0)),((y^2 =16)) :} since y^2 +4×5=36>0 x∈{((−y±(√(y^2 −4×5)))/2)} so: S⇔ { ((x∈{−y/2±3})),((y^2 =16)) :} S⇔ { ((x∈{−2±3,2±3})),((y^2 =16)) :} S⇒ { ((x^2 ∈{2^2 ±2×2×3+3^2 })),((y^2 =16)) :}I just developped (a±b)^2 thus S⇒ { ((x^2 ∈{13±12})),((y^2 =16)) :} so S⇒x^2 +y^2 ∈{17,41}_■ By the way (this has nothing to do with the question) those are two elipses so the number of solutions for (x,y) less (or equal) to 4 the two elispes beeing centered on (0,0) the set of solutions is symetrical that is to say that if (x,y) is solution (x,y) is too. you can then randomly try some values and notice that : (x,y)=(1,4) and (x,y)=(5,−4) are solutions so you have directly what you wanted this method is not as great as what I first did. because is relies on you making a lucky guess however if you have access to geogebra (or some equivalent) this makes the problem trivial plus, you can mix the methods. (for instance, once I have reached y^2 =16 with the first method, you might want to check for obvious values of x) I hope you find that note interesting :−)
$$\mathrm{let}\:\mathrm{S}=\begin{cases}{{x}^{\mathrm{2}} +\mathrm{2}{y}^{\mathrm{2}} +{xy}=\mathrm{37}}\\{{y}^{\mathrm{2}} +\mathrm{2}{x}^{\mathrm{2}} +\mathrm{2}{xy}=\mathrm{26}}\end{cases} \\ $$$$\Leftrightarrow\begin{cases}{{x}^{\mathrm{2}} +\mathrm{2}{y}^{\mathrm{2}} +{xy}=\mathrm{37}}\\{−\mathrm{3}{y}^{\mathrm{2}} =\mathrm{26}−\mathrm{2}×\mathrm{37}}\end{cases} \\ $$$$\Leftrightarrow\begin{cases}{{x}^{\mathrm{2}} +\mathrm{2}{y}^{\mathrm{2}} +{xy}=\mathrm{37}}\\{{y}^{\mathrm{2}} =\mathrm{16}}\end{cases} \\ $$$$\Leftrightarrow\begin{cases}{{x}^{\mathrm{2}} +\mathrm{32}+{xy}=\mathrm{37}}\\{{y}^{\mathrm{2}} =\mathrm{16}}\end{cases} \\ $$$$\Leftrightarrow\begin{cases}{{x}^{\mathrm{2}} +{xy}−\mathrm{5}=\mathrm{0}}\\{{y}^{\mathrm{2}} =\mathrm{16}}\end{cases} \\ $$$$\mathrm{since}\:{y}^{\mathrm{2}} +\mathrm{4}×\mathrm{5}=\mathrm{36}>\mathrm{0}\:{x}\in\left\{\frac{−{y}\pm\sqrt{{y}^{\mathrm{2}} −\mathrm{4}×\mathrm{5}}}{\mathrm{2}}\right\} \\ $$$$\mathrm{so}: \\ $$$$\mathrm{S}\Leftrightarrow\begin{cases}{{x}\in\left\{−{y}/\mathrm{2}\pm\mathrm{3}\right\}}\\{{y}^{\mathrm{2}} =\mathrm{16}}\end{cases} \\ $$$$\mathrm{S}\Leftrightarrow\begin{cases}{{x}\in\left\{−\mathrm{2}\pm\mathrm{3},\mathrm{2}\pm\mathrm{3}\right\}}\\{{y}^{\mathrm{2}} =\mathrm{16}}\end{cases} \\ $$$$\mathrm{S}\Rightarrow\begin{cases}{{x}^{\mathrm{2}} \in\left\{\mathrm{2}^{\mathrm{2}} \pm\mathrm{2}×\mathrm{2}×\mathrm{3}+\mathrm{3}^{\mathrm{2}} \right\}}\\{{y}^{\mathrm{2}} =\mathrm{16}}\end{cases}{I}\:{just}\:{developped}\:\left({a}\pm{b}\right)^{\mathrm{2}} \\ $$$$\mathrm{thus}\:\mathrm{S}\Rightarrow\begin{cases}{{x}^{\mathrm{2}} \in\left\{\mathrm{13}\pm\mathrm{12}\right\}}\\{{y}^{\mathrm{2}} =\mathrm{16}}\end{cases} \\ $$$$\mathrm{so}\:\mathrm{S}\Rightarrow{x}^{\mathrm{2}} +{y}^{\mathrm{2}} \in\left\{\mathrm{17},\mathrm{41}\right\}_{\blacksquare} \\ $$$$ \\ $$$$ \\ $$$${By}\:{the}\:{way}\:\left({this}\:{has}\:{nothing}\:{to}\:{do}\:{with}\:{the}\:{question}\right) \\ $$$${those}\:{are}\:{two}\:{elipses}\:{so}\:{the}\:{number}\:{of}\:{solutions}\:{for}\:\left({x},{y}\right)\:{less}\:\left({or}\:{equal}\right)\:{to}\:\mathrm{4} \\ $$$${the}\:{two}\:{elispes}\:{beeing}\:{centered}\:{on}\:\left(\mathrm{0},\mathrm{0}\right)\:{the}\:{set}\:{of}\:{solutions}\:{is}\:{symetrical} \\ $$$$\mathrm{that}\:\mathrm{is}\:\mathrm{to}\:\mathrm{say}\:\mathrm{that}\:\mathrm{if}\:\left({x},{y}\right)\:\mathrm{is}\:\mathrm{solution}\:\left({x},{y}\right)\:\mathrm{is}\:\mathrm{too}. \\ $$$${you}\:{can}\:{then}\:{randomly}\:{try}\:{some}\:{values}\:{and}\:{notice}\:{that}\:: \\ $$$$\left({x},{y}\right)=\left(\mathrm{1},\mathrm{4}\right)\:{and}\:\left({x},{y}\right)=\left(\mathrm{5},−\mathrm{4}\right)\:{are}\:{solutions} \\ $$$${so}\:{you}\:{have}\:{directly}\:{what}\:{you}\:{wanted} \\ $$$$ \\ $$$${this}\:{method}\:{is}\:{not}\:{as}\:{great}\:{as}\:{what}\:{I}\:{first}\:{did}. \\ $$$${because}\:{is}\:{relies}\:{on}\:{you}\:{making}\:{a}\:{lucky}\:{guess} \\ $$$${however}\:{if}\:{you}\:{have}\:{access}\:{to}\:{geogebra}\:\left({or}\:{some}\:{equivalent}\right)\:{this}\:{makes}\:{the}\:{problem}\:{trivial} \\ $$$$ \\ $$$${plus},\:{you}\:{can}\:{mix}\:{the}\:{methods}. \\ $$$$\left({for}\:{instance},\:{once}\:{I}\:{have}\:{reached}\:{y}^{\mathrm{2}} =\mathrm{16}\:{with}\:{the}\:{first}\:{method},\:{you}\:{might}\:{want}\:{to}\:{check}\:{for}\:{obvious}\:{values}\:{of}\:{x}\right) \\ $$$$ \\ $$$$ \\ $$$${I}\:{hope}\:{you}\:{find}\:{that}\:{note}\:{interesting} \\ $$$$\left.:−\right) \\ $$
Commented by mathdanisur last updated on 16/Jul/21
thank you Ser
$${thank}\:{you}\:{Ser} \\ $$
Answered by mr W last updated on 16/Jul/21
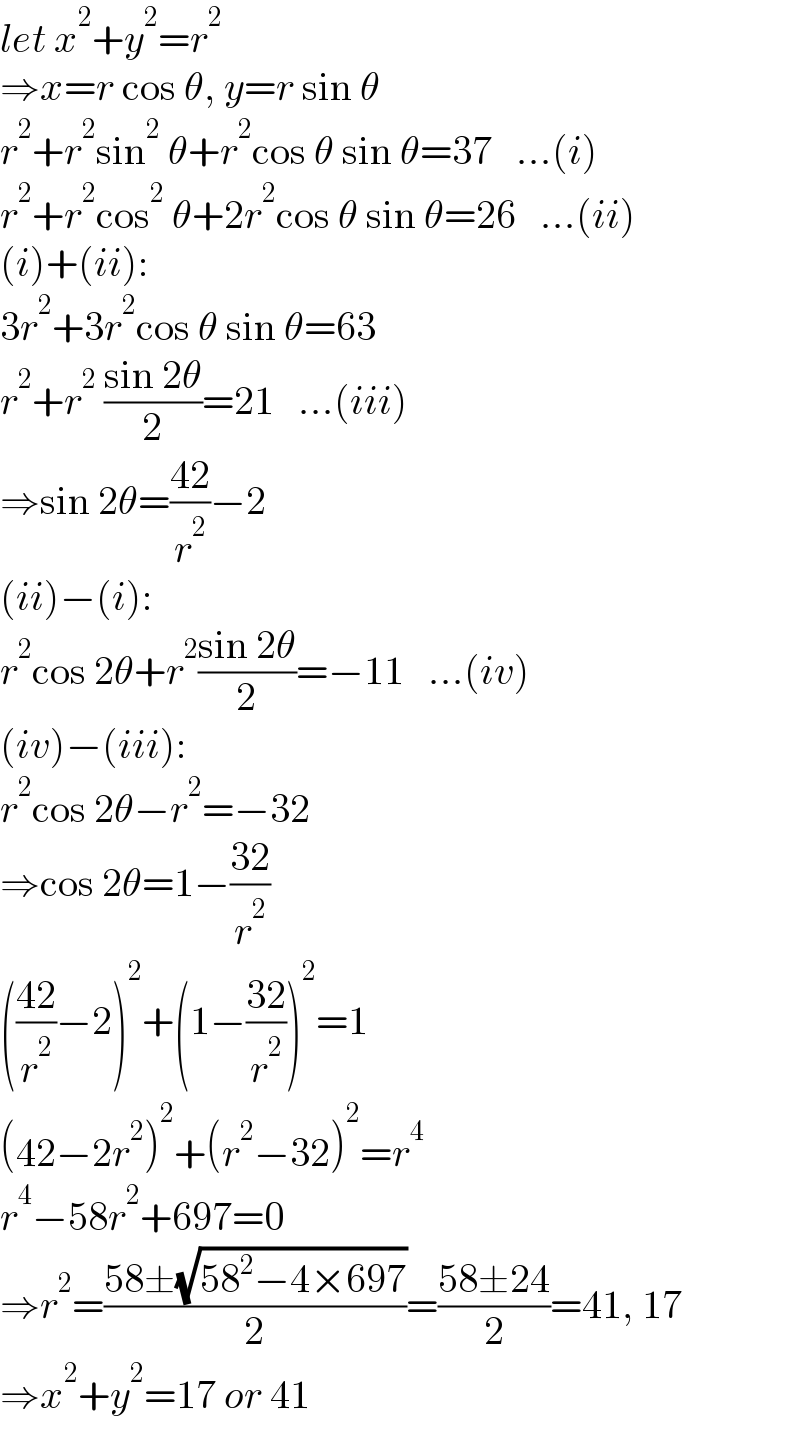
let x^2 +y^2 =r^2 ⇒x=r cos θ, y=r sin θ r^2 +r^2 sin^2 θ+r^2 cos θ sin θ=37 ...(i) r^2 +r^2 cos^2 θ+2r^2 cos θ sin θ=26 ...(ii) (i)+(ii): 3r^2 +3r^2 cos θ sin θ=63 r^2 +r^2 ((sin 2θ)/2)=21 ...(iii) ⇒sin 2θ=((42)/r^2 )−2 (ii)−(i): r^2 cos 2θ+r^2 ((sin 2θ)/2)=−11 ...(iv) (iv)−(iii): r^2 cos 2θ−r^2 =−32 ⇒cos 2θ=1−((32)/r^2 ) (((42)/r^2 )−2)^2 +(1−((32)/r^2 ))^2 =1 (42−2r^2 )^2 +(r^2 −32)^2 =r^4 r^4 −58r^2 +697=0 ⇒r^2 =((58±(√(58^2 −4×697)))/2)=((58±24)/2)=41, 17 ⇒x^2 +y^2 =17 or 41
$${let}\:{x}^{\mathrm{2}} +{y}^{\mathrm{2}} ={r}^{\mathrm{2}} \\ $$$$\Rightarrow{x}={r}\:\mathrm{cos}\:\theta,\:{y}={r}\:\mathrm{sin}\:\theta \\ $$$${r}^{\mathrm{2}} +{r}^{\mathrm{2}} \mathrm{sin}^{\mathrm{2}} \:\theta+{r}^{\mathrm{2}} \mathrm{cos}\:\theta\:\mathrm{sin}\:\theta=\mathrm{37}\:\:\:…\left({i}\right) \\ $$$${r}^{\mathrm{2}} +{r}^{\mathrm{2}} \mathrm{cos}^{\mathrm{2}} \:\theta+\mathrm{2}{r}^{\mathrm{2}} \mathrm{cos}\:\theta\:\mathrm{sin}\:\theta=\mathrm{26}\:\:\:…\left({ii}\right) \\ $$$$\left({i}\right)+\left({ii}\right): \\ $$$$\mathrm{3}{r}^{\mathrm{2}} +\mathrm{3}{r}^{\mathrm{2}} \mathrm{cos}\:\theta\:\mathrm{sin}\:\theta=\mathrm{63} \\ $$$${r}^{\mathrm{2}} +{r}^{\mathrm{2}} \:\frac{\mathrm{sin}\:\mathrm{2}\theta}{\mathrm{2}}=\mathrm{21}\:\:\:…\left({iii}\right) \\ $$$$\Rightarrow\mathrm{sin}\:\mathrm{2}\theta=\frac{\mathrm{42}}{{r}^{\mathrm{2}} }−\mathrm{2} \\ $$$$\left({ii}\right)−\left({i}\right): \\ $$$${r}^{\mathrm{2}} \mathrm{cos}\:\mathrm{2}\theta+{r}^{\mathrm{2}} \frac{\mathrm{sin}\:\mathrm{2}\theta}{\mathrm{2}}=−\mathrm{11}\:\:\:…\left({iv}\right) \\ $$$$\left({iv}\right)−\left({iii}\right): \\ $$$${r}^{\mathrm{2}} \mathrm{cos}\:\mathrm{2}\theta−{r}^{\mathrm{2}} =−\mathrm{32} \\ $$$$\Rightarrow\mathrm{cos}\:\mathrm{2}\theta=\mathrm{1}−\frac{\mathrm{32}}{{r}^{\mathrm{2}} } \\ $$$$\left(\frac{\mathrm{42}}{{r}^{\mathrm{2}} }−\mathrm{2}\right)^{\mathrm{2}} +\left(\mathrm{1}−\frac{\mathrm{32}}{{r}^{\mathrm{2}} }\right)^{\mathrm{2}} =\mathrm{1} \\ $$$$\left(\mathrm{42}−\mathrm{2}{r}^{\mathrm{2}} \right)^{\mathrm{2}} +\left({r}^{\mathrm{2}} −\mathrm{32}\right)^{\mathrm{2}} ={r}^{\mathrm{4}} \\ $$$${r}^{\mathrm{4}} −\mathrm{58}{r}^{\mathrm{2}} +\mathrm{697}=\mathrm{0} \\ $$$$\Rightarrow{r}^{\mathrm{2}} =\frac{\mathrm{58}\pm\sqrt{\mathrm{58}^{\mathrm{2}} −\mathrm{4}×\mathrm{697}}}{\mathrm{2}}=\frac{\mathrm{58}\pm\mathrm{24}}{\mathrm{2}}=\mathrm{41},\:\mathrm{17} \\ $$$$\Rightarrow{x}^{\mathrm{2}} +{y}^{\mathrm{2}} =\mathrm{17}\:{or}\:\mathrm{41} \\ $$
Commented by behi834171 last updated on 16/Jul/21
very nice dear master!
$${very}\:{nice}\:{dear}\:{master}! \\ $$
Commented by mathdanisur last updated on 16/Jul/21
thank you Ser cool
$${thank}\:{you}\:{Ser}\:{cool} \\ $$
Commented by Tawa11 last updated on 23/Jul/21
great
$$\mathrm{great} \\ $$
Answered by behi834171 last updated on 17/Jul/21
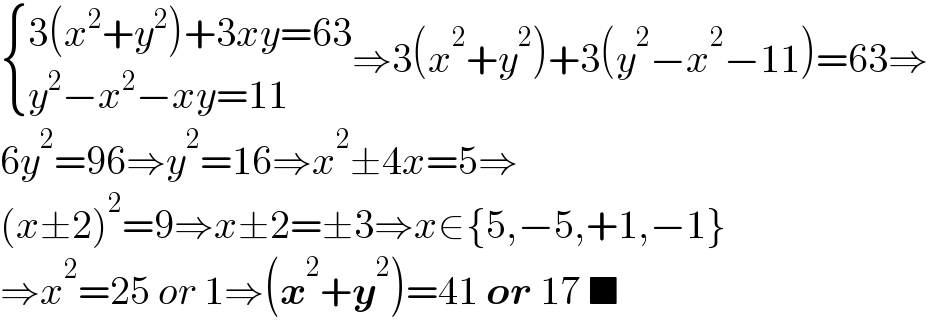
{ ((3(x^2 +y^2 )+3xy=63)),((y^2 −x^2 −xy=11)) :}⇒3(x^2 +y^2 )+3(y^2 −x^2 −11)=63⇒ 6y^2 =96⇒y^2 =16⇒x^2 ±4x=5⇒ (x±2)^2 =9⇒x±2=±3⇒x∈{5,−5,+1,−1} ⇒x^2 =25 or 1⇒(x^2 +y^2 )=41 or 17 ■
$$\begin{cases}{\mathrm{3}\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} \right)+\mathrm{3}{xy}=\mathrm{63}}\\{{y}^{\mathrm{2}} −{x}^{\mathrm{2}} −{xy}=\mathrm{11}}\end{cases}\Rightarrow\mathrm{3}\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} \right)+\mathrm{3}\left({y}^{\mathrm{2}} −{x}^{\mathrm{2}} −\mathrm{11}\right)=\mathrm{63}\Rightarrow \\ $$$$\mathrm{6}{y}^{\mathrm{2}} =\mathrm{96}\Rightarrow{y}^{\mathrm{2}} =\mathrm{16}\Rightarrow{x}^{\mathrm{2}} \pm\mathrm{4}{x}=\mathrm{5}\Rightarrow \\ $$$$\left({x}\pm\mathrm{2}\right)^{\mathrm{2}} =\mathrm{9}\Rightarrow{x}\pm\mathrm{2}=\pm\mathrm{3}\Rightarrow{x}\in\left\{\mathrm{5},−\mathrm{5},+\mathrm{1},−\mathrm{1}\right\} \\ $$$$\Rightarrow{x}^{\mathrm{2}} =\mathrm{25}\:{or}\:\mathrm{1}\Rightarrow\left(\boldsymbol{{x}}^{\mathrm{2}} +\boldsymbol{{y}}^{\mathrm{2}} \right)=\mathrm{41}\:\boldsymbol{{or}}\:\mathrm{17}\:\blacksquare \\ $$
Commented by mathdanisur last updated on 16/Jul/21
thanks Ser cool
$${thanks}\:{Ser}\:{cool} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *