Question Number 166610 by cortano1 last updated on 23/Feb/22
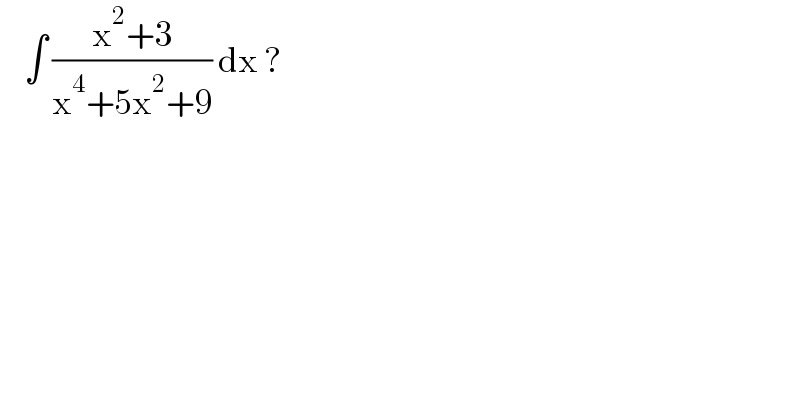
$$\:\:\:\:\int\:\frac{\mathrm{x}^{\mathrm{2}} +\mathrm{3}}{\mathrm{x}^{\mathrm{4}} +\mathrm{5x}^{\mathrm{2}} +\mathrm{9}}\:\mathrm{dx}\:? \\ $$
Commented by MJS_new last updated on 23/Feb/22
![in this case: (d/dx)[(1/a)arctan ((ax)/(b−x^2 ))]=((x^2 +b)/(x^4 +(a^2 −2b)x^2 +b^2 )) with a=(√(11)) ∧ b=3 ⇒ ∫((x^2 +3)/(x^4 +5x^2 +9))dx=(1/( (√(11))))arctan (((√(11))x)/(3−x^2 )) +C](https://www.tinkutara.com/question/Q166636.png)
$$\mathrm{in}\:\mathrm{this}\:\mathrm{case}: \\ $$$$\frac{{d}}{{dx}}\left[\frac{\mathrm{1}}{{a}}\mathrm{arctan}\:\frac{{ax}}{{b}−{x}^{\mathrm{2}} }\right]=\frac{{x}^{\mathrm{2}} +{b}}{{x}^{\mathrm{4}} +\left({a}^{\mathrm{2}} −\mathrm{2}{b}\right){x}^{\mathrm{2}} +{b}^{\mathrm{2}} } \\ $$$$\mathrm{with}\:{a}=\sqrt{\mathrm{11}}\:\wedge\:{b}=\mathrm{3} \\ $$$$\Rightarrow\:\int\frac{{x}^{\mathrm{2}} +\mathrm{3}}{{x}^{\mathrm{4}} +\mathrm{5}{x}^{\mathrm{2}} +\mathrm{9}}{dx}=\frac{\mathrm{1}}{\:\sqrt{\mathrm{11}}}\mathrm{arctan}\:\frac{\sqrt{\mathrm{11}}{x}}{\mathrm{3}−{x}^{\mathrm{2}} }\:+{C} \\ $$
Answered by MJS_new last updated on 23/Feb/22
![∫((x^2 +3)/(x^4 +5x^2 +9))dx=(1/2)∫(dx/(x^2 −x+3))+(1/2)∫(dx/(x^2 +x+3))= [use commom formula] =((√(11))/(11))(arctan ((2x−1)/( (√(11)))) +arctan ((2x+1)/( (√(11)))))+C](https://www.tinkutara.com/question/Q166635.png)
$$\int\frac{{x}^{\mathrm{2}} +\mathrm{3}}{{x}^{\mathrm{4}} +\mathrm{5}{x}^{\mathrm{2}} +\mathrm{9}}{dx}=\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{dx}}{{x}^{\mathrm{2}} −{x}+\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{dx}}{{x}^{\mathrm{2}} +{x}+\mathrm{3}}= \\ $$$$\:\:\:\:\:\left[\mathrm{use}\:\mathrm{commom}\:\mathrm{formula}\right] \\ $$$$=\frac{\sqrt{\mathrm{11}}}{\mathrm{11}}\left(\mathrm{arctan}\:\frac{\mathrm{2}{x}−\mathrm{1}}{\:\sqrt{\mathrm{11}}}\:+\mathrm{arctan}\:\frac{\mathrm{2}{x}+\mathrm{1}}{\:\sqrt{\mathrm{11}}}\right)+{C} \\ $$
Commented by cortano1 last updated on 25/Feb/22

$$\mathrm{nice} \\ $$
