Menu Close

x-2-3xy-y-2-1-x-3-y-3-7-

Tinku Tara 0 Comments
Pin




Question Number 112287 by weltr last updated on 07/Sep/20
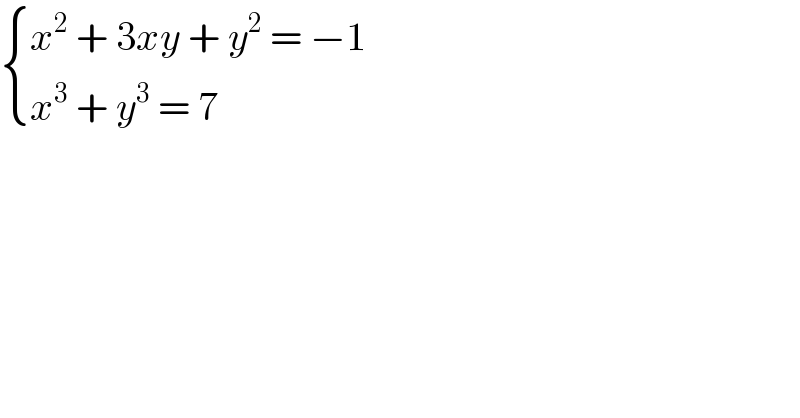
{ ((x^2 + 3xy + y^2 = −1)),((x^3 + y^3 = 7)) :}
$$\begin{cases}{{x}^{\mathrm{2}} \:+\:\mathrm{3}{xy}\:+\:{y}^{\mathrm{2}} \:=\:−\mathrm{1}}\\{{x}^{\mathrm{3}} \:+\:{y}^{\mathrm{3}} \:=\:\mathrm{7}}\end{cases} \\ $$
Answered by ajfour last updated on 07/Sep/20
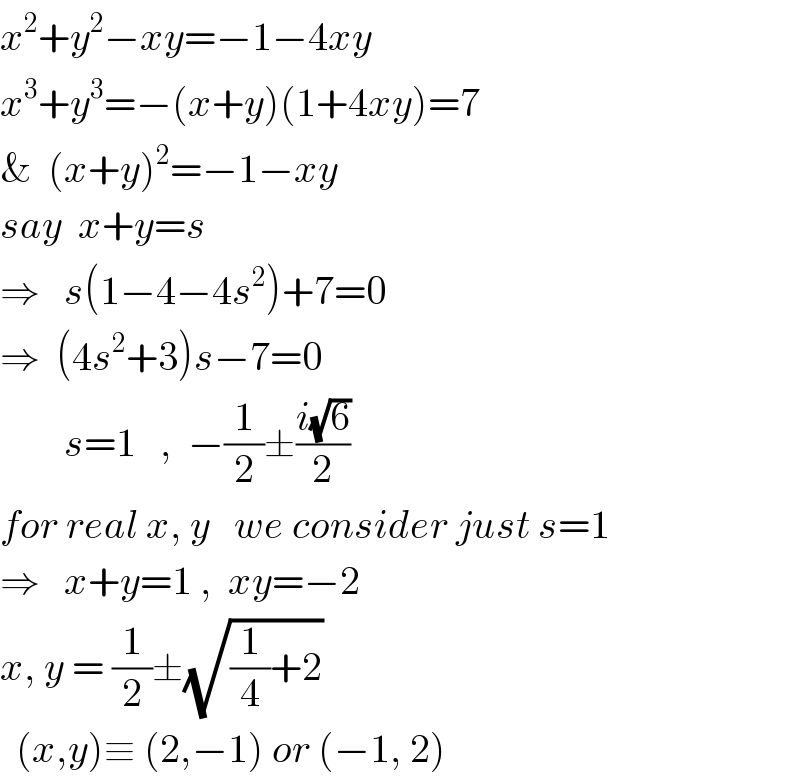
x^2 +y^2 −xy=−1−4xy x^3 +y^3 =−(x+y)(1+4xy)=7 & (x+y)^2 =−1−xy say x+y=s ⇒ s(1−4−4s^2 )+7=0 ⇒ (4s^2 +3)s−7=0 s=1 , −(1/2)±((i(√6))/2) for real x, y we consider just s=1 ⇒ x+y=1 , xy=−2 x, y = (1/2)±(√((1/4)+2)) (x,y)≡ (2,−1) or (−1, 2)
$${x}^{\mathrm{2}} +{y}^{\mathrm{2}} −{xy}=−\mathrm{1}−\mathrm{4}{xy} \\ $$$${x}^{\mathrm{3}} +{y}^{\mathrm{3}} =−\left({x}+{y}\right)\left(\mathrm{1}+\mathrm{4}{xy}\right)=\mathrm{7} \\ $$$$\&\:\:\left({x}+{y}\right)^{\mathrm{2}} =−\mathrm{1}−{xy} \\ $$$${say}\:\:{x}+{y}={s} \\ $$$$\Rightarrow\:\:\:{s}\left(\mathrm{1}−\mathrm{4}−\mathrm{4}{s}^{\mathrm{2}} \right)+\mathrm{7}=\mathrm{0} \\ $$$$\Rightarrow\:\:\left(\mathrm{4}{s}^{\mathrm{2}} +\mathrm{3}\right){s}−\mathrm{7}=\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:{s}=\mathrm{1}\:\:\:,\:\:−\frac{\mathrm{1}}{\mathrm{2}}\pm\frac{{i}\sqrt{\mathrm{6}}}{\mathrm{2}} \\ $$$${for}\:{real}\:{x},\:{y}\:\:\:{we}\:{consider}\:{just}\:{s}=\mathrm{1} \\ $$$$\Rightarrow\:\:\:{x}+{y}=\mathrm{1}\:,\:\:{xy}=−\mathrm{2} \\ $$$${x},\:{y}\:=\:\frac{\mathrm{1}}{\mathrm{2}}\pm\sqrt{\frac{\mathrm{1}}{\mathrm{4}}+\mathrm{2}} \\ $$$$\:\:\left({x},{y}\right)\equiv\:\left(\mathrm{2},−\mathrm{1}\right)\:{or}\:\left(−\mathrm{1},\:\mathrm{2}\right) \\ $$
Answered by MJS_new last updated on 07/Sep/20
let x=u−(√v)∧y=u+(√v) { ((5u^2 −v=−1 ⇒ v=5u^2 +1)),((2u^3 +6uv=7 ⇒ v=−((2u^3 −7)/(6u)))) :} 5u^2 +1=−((2u^3 −7)/(6u)) u^3 +(3/(16))u−(7/(32))=0 (u−(1/2))(u^2 +(1/2)u+(7/(16)))=0 u_1 =(1/2) u_(2, 3) =−(1/4)±((√6)/4)i v_1 =(9/4) v_(2, 3) =−(9/(16))∓((5(√6))/8)i x_1 =−1 y_1 =2 x_(2, 3) =−((2+(√(−18+2(√(681)))))/8)±((2(√6)+(√(18+2(√(681)))))/8)i y_(2, 3) =−((2−(√(−18+2(√(681)))))/8)±((2(√6)−(√(18+2(√(681)))))/8)i and of course we can exchange x with y due to symmetry
$$\mathrm{let}\:{x}={u}−\sqrt{{v}}\wedge{y}={u}+\sqrt{{v}} \\ $$$$\begin{cases}{\mathrm{5}{u}^{\mathrm{2}} −{v}=−\mathrm{1}\:\Rightarrow\:{v}=\mathrm{5}{u}^{\mathrm{2}} +\mathrm{1}}\\{\mathrm{2}{u}^{\mathrm{3}} +\mathrm{6}{uv}=\mathrm{7}\:\Rightarrow\:{v}=−\frac{\mathrm{2}{u}^{\mathrm{3}} −\mathrm{7}}{\mathrm{6}{u}}}\end{cases} \\ $$$$\mathrm{5}{u}^{\mathrm{2}} +\mathrm{1}=−\frac{\mathrm{2}{u}^{\mathrm{3}} −\mathrm{7}}{\mathrm{6}{u}} \\ $$$${u}^{\mathrm{3}} +\frac{\mathrm{3}}{\mathrm{16}}{u}−\frac{\mathrm{7}}{\mathrm{32}}=\mathrm{0} \\ $$$$\left({u}−\frac{\mathrm{1}}{\mathrm{2}}\right)\left({u}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{2}}{u}+\frac{\mathrm{7}}{\mathrm{16}}\right)=\mathrm{0} \\ $$$${u}_{\mathrm{1}} =\frac{\mathrm{1}}{\mathrm{2}}\:\:{u}_{\mathrm{2},\:\mathrm{3}} =−\frac{\mathrm{1}}{\mathrm{4}}\pm\frac{\sqrt{\mathrm{6}}}{\mathrm{4}}\mathrm{i} \\ $$$${v}_{\mathrm{1}} =\frac{\mathrm{9}}{\mathrm{4}}\:\:{v}_{\mathrm{2},\:\mathrm{3}} =−\frac{\mathrm{9}}{\mathrm{16}}\mp\frac{\mathrm{5}\sqrt{\mathrm{6}}}{\mathrm{8}}\mathrm{i} \\ $$$${x}_{\mathrm{1}} =−\mathrm{1}\:\:{y}_{\mathrm{1}} =\mathrm{2} \\ $$$${x}_{\mathrm{2},\:\mathrm{3}} =−\frac{\mathrm{2}+\sqrt{−\mathrm{18}+\mathrm{2}\sqrt{\mathrm{681}}}}{\mathrm{8}}\pm\frac{\mathrm{2}\sqrt{\mathrm{6}}+\sqrt{\mathrm{18}+\mathrm{2}\sqrt{\mathrm{681}}}}{\mathrm{8}}\mathrm{i} \\ $$$${y}_{\mathrm{2},\:\mathrm{3}} =−\frac{\mathrm{2}−\sqrt{−\mathrm{18}+\mathrm{2}\sqrt{\mathrm{681}}}}{\mathrm{8}}\pm\frac{\mathrm{2}\sqrt{\mathrm{6}}−\sqrt{\mathrm{18}+\mathrm{2}\sqrt{\mathrm{681}}}}{\mathrm{8}}\mathrm{i} \\ $$$$\mathrm{and}\:\mathrm{of}\:\mathrm{course}\:\mathrm{we}\:\mathrm{can}\:\mathrm{exchange}\:{x}\:\mathrm{with}\:{y}\:\mathrm{due} \\ $$$$\mathrm{to}\:\mathrm{symmetry} \\ $$
Answered by bemath last updated on 07/Sep/20
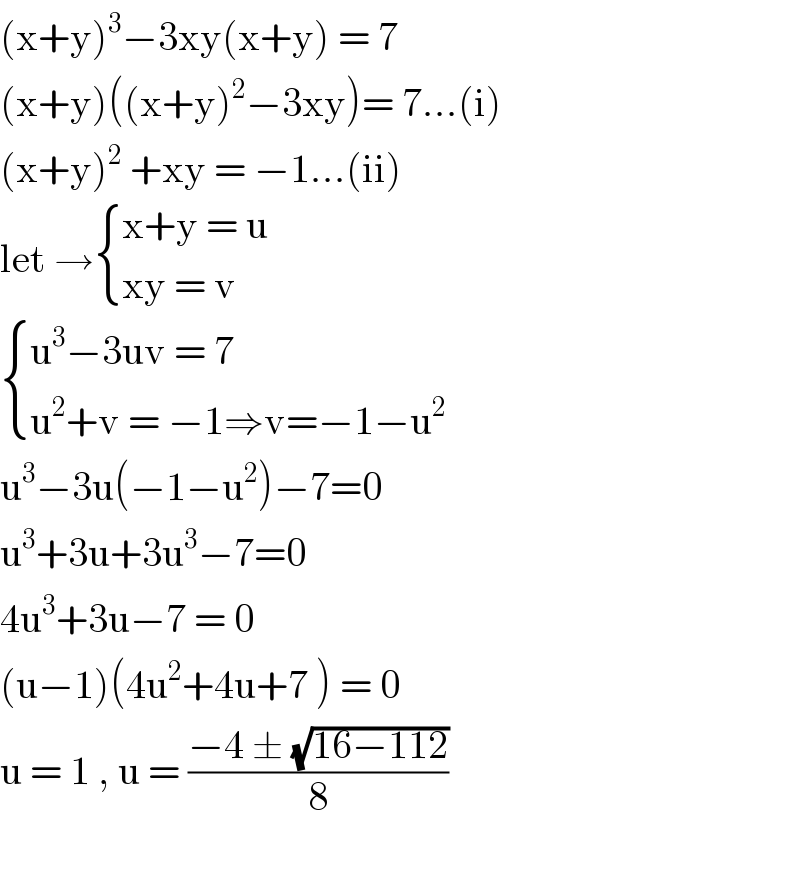
(x+y)^3 −3xy(x+y) = 7 (x+y)((x+y)^2 −3xy)= 7...(i) (x+y)^2 +xy = −1...(ii) let → { ((x+y = u)),((xy = v)) :} { ((u^3 −3uv = 7)),((u^2 +v = −1⇒v=−1−u^2 )) :} u^3 −3u(−1−u^2 )−7=0 u^3 +3u+3u^3 −7=0 4u^3 +3u−7 = 0 (u−1)(4u^2 +4u+7 ) = 0 u = 1 , u = ((−4 ± (√(16−112)))/8)
$$\left(\mathrm{x}+\mathrm{y}\right)^{\mathrm{3}} −\mathrm{3xy}\left(\mathrm{x}+\mathrm{y}\right)\:=\:\mathrm{7} \\ $$$$\left(\mathrm{x}+\mathrm{y}\right)\left(\left(\mathrm{x}+\mathrm{y}\right)^{\mathrm{2}} −\mathrm{3xy}\right)=\:\mathrm{7}…\left(\mathrm{i}\right) \\ $$$$\left(\mathrm{x}+\mathrm{y}\right)^{\mathrm{2}} \:+\mathrm{xy}\:=\:−\mathrm{1}…\left(\mathrm{ii}\right) \\ $$$$\mathrm{let}\:\rightarrow\begin{cases}{\mathrm{x}+\mathrm{y}\:=\:\mathrm{u}}\\{\mathrm{xy}\:=\:\mathrm{v}}\end{cases} \\ $$$$\begin{cases}{\mathrm{u}^{\mathrm{3}} −\mathrm{3uv}\:=\:\mathrm{7}}\\{\mathrm{u}^{\mathrm{2}} +\mathrm{v}\:=\:−\mathrm{1}\Rightarrow\mathrm{v}=−\mathrm{1}−\mathrm{u}^{\mathrm{2}} }\end{cases} \\ $$$$\mathrm{u}^{\mathrm{3}} −\mathrm{3u}\left(−\mathrm{1}−\mathrm{u}^{\mathrm{2}} \right)−\mathrm{7}=\mathrm{0} \\ $$$$\mathrm{u}^{\mathrm{3}} +\mathrm{3u}+\mathrm{3u}^{\mathrm{3}} −\mathrm{7}=\mathrm{0} \\ $$$$\mathrm{4u}^{\mathrm{3}} +\mathrm{3u}−\mathrm{7}\:=\:\mathrm{0} \\ $$$$\left(\mathrm{u}−\mathrm{1}\right)\left(\mathrm{4u}^{\mathrm{2}} +\mathrm{4u}+\mathrm{7}\:\right)\:=\:\mathrm{0} \\ $$$$\mathrm{u}\:=\:\mathrm{1}\:,\:\mathrm{u}\:=\:\frac{−\mathrm{4}\:\pm\:\sqrt{\mathrm{16}−\mathrm{112}}}{\mathrm{8}} \\ $$$$ \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *