Question Number 168335 by vbr last updated on 08/Apr/22
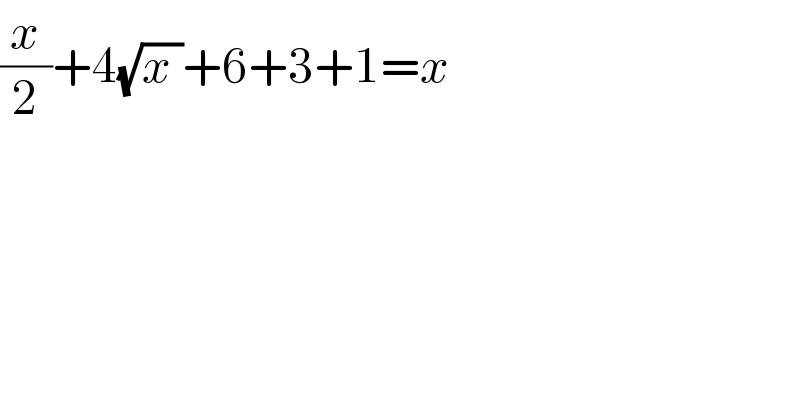
$$\frac{{x}}{\mathrm{2}}+\mathrm{4}\sqrt{{x}\:}+\mathrm{6}+\mathrm{3}+\mathrm{1}={x} \\ $$
Answered by Rasheed.Sindhi last updated on 08/Apr/22
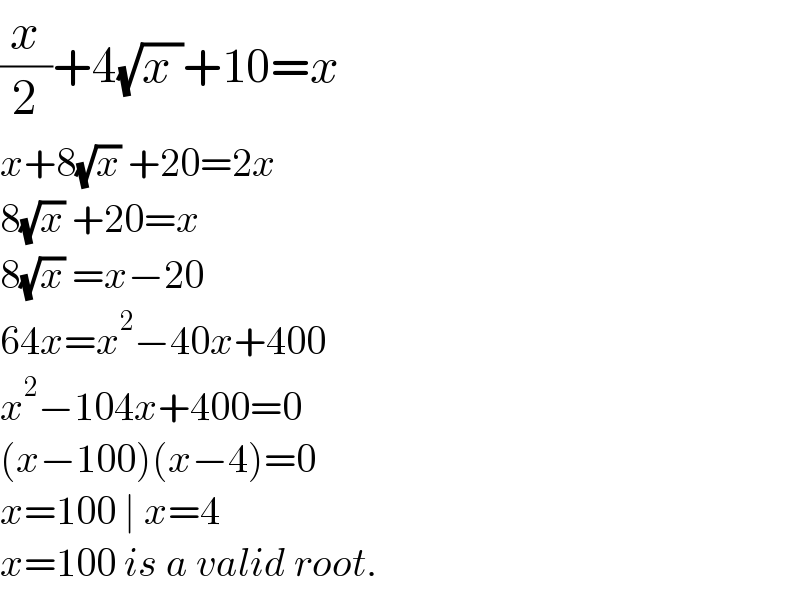
$$\frac{{x}}{\mathrm{2}}+\mathrm{4}\sqrt{{x}\:}+\mathrm{10}={x} \\ $$$${x}+\mathrm{8}\sqrt{{x}}\:+\mathrm{20}=\mathrm{2}{x} \\ $$$$\mathrm{8}\sqrt{{x}}\:+\mathrm{20}={x} \\ $$$$\mathrm{8}\sqrt{{x}}\:={x}−\mathrm{20} \\ $$$$\mathrm{64}{x}={x}^{\mathrm{2}} −\mathrm{40}{x}+\mathrm{400} \\ $$$${x}^{\mathrm{2}} −\mathrm{104}{x}+\mathrm{400}=\mathrm{0} \\ $$$$\left({x}−\mathrm{100}\right)\left({x}−\mathrm{4}\right)=\mathrm{0} \\ $$$${x}=\mathrm{100}\:\mid\:{x}=\mathrm{4} \\ $$$${x}=\mathrm{100}\:{is}\:{a}\:{valid}\:{root}. \\ $$
Answered by mr W last updated on 08/Apr/22
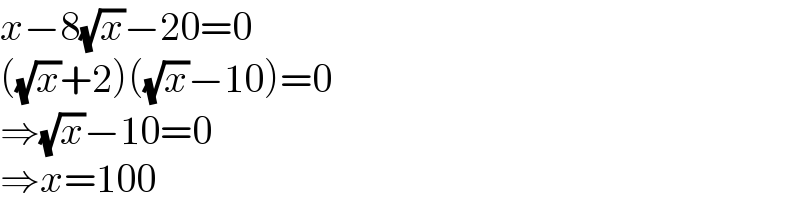
$${x}−\mathrm{8}\sqrt{{x}}−\mathrm{20}=\mathrm{0} \\ $$$$\left(\sqrt{{x}}+\mathrm{2}\right)\left(\sqrt{{x}}−\mathrm{10}\right)=\mathrm{0} \\ $$$$\Rightarrow\sqrt{{x}}−\mathrm{10}=\mathrm{0} \\ $$$$\Rightarrow{x}=\mathrm{100} \\ $$
