Question Number 162174 by mnjuly1970 last updated on 27/Dec/21

$$ \\ $$$$\:\:\:\:{x}^{\:\mathrm{2}} −\:\mathrm{4}{x}\:−\mathrm{1}=\mathrm{0}\:\: \\ $$$$\:\:\:\:\:\alpha\:,\:\beta\:\:{are}\:{roots}\: \\ $$$$\:\:\:\:\:\alpha^{\:\mathrm{3}} \:+\:\mathrm{17}\beta\:+\mathrm{5}\:=? \\ $$$$\:\:−−−{solution}−−− \\ $$$$\:\:\:\alpha\:\:\:{is}\:{root}\:\:\:\Rightarrow\:\alpha^{\:\mathrm{2}} −\mathrm{4}\alpha\:−\mathrm{1}=\mathrm{0} \\ $$$$\:\:\:\:\:\Rightarrow\:\alpha^{\:\mathrm{2}} =\:\mathrm{4}\alpha\:+\mathrm{1}\:\:\checkmark \\ $$$$\:\:\:\:\:\:\alpha^{\:\mathrm{3}} +\:\mathrm{17}\beta\:+\mathrm{5}\:=\:\alpha\:.\:\alpha^{\:\mathrm{2}} +\mathrm{17}\beta\:+\mathrm{5} \\ $$$$\:\:=\:\alpha\:\left(\:\mathrm{4}\alpha\:+\mathrm{1}\:\right)+\:\mathrm{17}\beta\:+\mathrm{5} \\ $$$$\:\:=\:\mathrm{4}\alpha^{\:\mathrm{2}} +\:\alpha\:+\:\mathrm{17}\beta\:+\mathrm{5} \\ $$$$\:\:=\:\mathrm{4}\:\left(\mathrm{4}\alpha\:+\mathrm{1}\:\right)+\alpha\:+\mathrm{17}\beta\:+\mathrm{5}=\mathrm{17}\left(\alpha+\beta\right)+\mathrm{9} \\ $$$$\:\:=\:\mathrm{17S}\:+\mathrm{9}=\:\mathrm{17}\:\left(\mathrm{4}\:\right)+\mathrm{9}=\mathrm{77} \\ $$$$ \\ $$
Commented by cortano last updated on 27/Dec/21
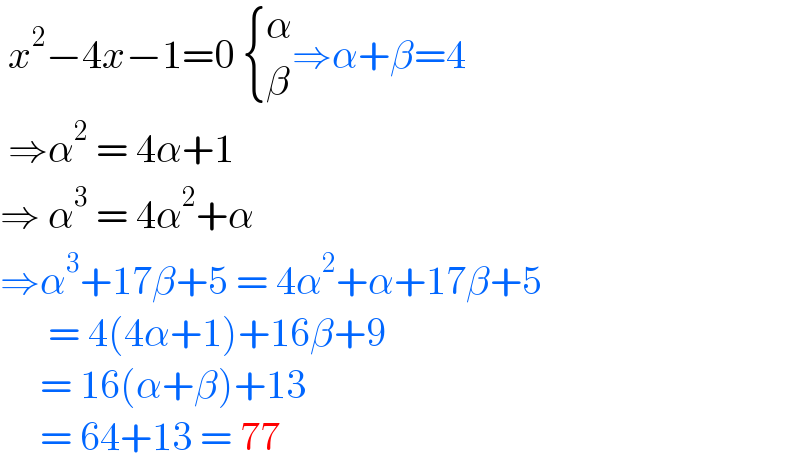
$$\:{x}^{\mathrm{2}} −\mathrm{4}{x}−\mathrm{1}=\mathrm{0}\:\begin{cases}{\alpha}\\{\beta}\end{cases}\Rightarrow\alpha+\beta=\mathrm{4} \\ $$$$\:\Rightarrow\alpha^{\mathrm{2}} \:=\:\mathrm{4}\alpha+\mathrm{1} \\ $$$$\Rightarrow\:\alpha^{\mathrm{3}} \:=\:\mathrm{4}\alpha^{\mathrm{2}} +\alpha \\ $$$$\Rightarrow\alpha^{\mathrm{3}} +\mathrm{17}\beta+\mathrm{5}\:=\:\mathrm{4}\alpha^{\mathrm{2}} +\alpha+\mathrm{17}\beta+\mathrm{5} \\ $$$$\:\:\:\:\:\:=\:\mathrm{4}\left(\mathrm{4}\alpha+\mathrm{1}\right)+\mathrm{16}\beta+\mathrm{9} \\ $$$$\:\:\:\:\:=\:\mathrm{16}\left(\alpha+\beta\right)+\mathrm{13} \\ $$$$\:\:\:\:\:=\:\mathrm{64}+\mathrm{13}\:=\:\mathrm{77}\: \\ $$
