Question Number 130337 by EDWIN88 last updated on 24/Jan/21

$$\:\left(\mathrm{x}^{\mathrm{2}} −\mathrm{4x}+\mathrm{3}\right)^{\mathrm{x}^{\mathrm{2}} −\mathrm{6x}+\mathrm{4}} \:\leqslant\:\mathrm{1}\: \\ $$
Answered by mathmax by abdo last updated on 24/Jan/21
![e⇒e^((x^2 −6x+4)ln(x^2 −4x+3)) ≤1 x^2 −4x+3=0→Δ^′ =4−3=1 ⇒x_1 =((2+1)/1)=3 and x_2 =((2−1)/1)=1 the equation is dfined on]−∞,1[∪]3,+∞[ e ⇒(x^2 −6x+4)ln(x^2 −4x+3)≤0 x^2 −6x+4=0→Δ^′ =9−4=5 ⇒x_1 =3+(√5) and x_2 =3−(√5) ln(x^2 −4x+3)>0 ⇒x^2 −4x+3>1 ⇒x^2 −4x+2>0 ⇒ x^2 −4x+4−2>0 ⇒(x−2)^2 −2>0 ⇒(x−2−(√2))(x−2+(√2))>0 ⇒ x∈]−∞,2−(√2)[∪]2+(√2),+∞[ ln(x^2 −4x+3)<0 ⇒x^2 −4x+3<1 ⇒x^2 −4x+2<0 ⇒ ]2−(√2),2+(√2)[ the problem lead to find sgn of (x^2 −6x+4)ln(x^2 −4x+3) ...be continued...](https://www.tinkutara.com/question/Q130341.png)
$$\mathrm{e}\Rightarrow\mathrm{e}^{\left(\mathrm{x}^{\mathrm{2}} −\mathrm{6x}+\mathrm{4}\right)\mathrm{ln}\left(\mathrm{x}^{\mathrm{2}} −\mathrm{4x}+\mathrm{3}\right)} \leqslant\mathrm{1} \\ $$$$\mathrm{x}^{\mathrm{2}} −\mathrm{4x}+\mathrm{3}=\mathrm{0}\rightarrow\Delta^{'} =\mathrm{4}−\mathrm{3}=\mathrm{1}\:\Rightarrow\mathrm{x}_{\mathrm{1}} =\frac{\mathrm{2}+\mathrm{1}}{\mathrm{1}}=\mathrm{3}\:\mathrm{and}\:\mathrm{x}_{\mathrm{2}} =\frac{\mathrm{2}−\mathrm{1}}{\mathrm{1}}=\mathrm{1} \\ $$$$\left.\mathrm{the}\:\mathrm{equation}\:\mathrm{is}\:\mathrm{dfined}\:\mathrm{on}\right]−\infty,\mathrm{1}\left[\cup\right]\mathrm{3},+\infty\left[\right. \\ $$$$\mathrm{e}\:\Rightarrow\left(\mathrm{x}^{\mathrm{2}} −\mathrm{6x}+\mathrm{4}\right)\mathrm{ln}\left(\mathrm{x}^{\mathrm{2}} −\mathrm{4x}+\mathrm{3}\right)\leqslant\mathrm{0} \\ $$$$\mathrm{x}^{\mathrm{2}} −\mathrm{6x}+\mathrm{4}=\mathrm{0}\rightarrow\Delta^{'} =\mathrm{9}−\mathrm{4}=\mathrm{5}\:\Rightarrow\mathrm{x}_{\mathrm{1}} =\mathrm{3}+\sqrt{\mathrm{5}}\:\mathrm{and}\:\mathrm{x}_{\mathrm{2}} =\mathrm{3}−\sqrt{\mathrm{5}} \\ $$$$\mathrm{ln}\left(\mathrm{x}^{\mathrm{2}} −\mathrm{4x}+\mathrm{3}\right)>\mathrm{0}\:\Rightarrow\mathrm{x}^{\mathrm{2}} −\mathrm{4x}+\mathrm{3}>\mathrm{1}\:\Rightarrow\mathrm{x}^{\mathrm{2}} −\mathrm{4x}+\mathrm{2}>\mathrm{0}\:\Rightarrow \\ $$$$\mathrm{x}^{\mathrm{2}} −\mathrm{4x}+\mathrm{4}−\mathrm{2}>\mathrm{0}\:\Rightarrow\left(\mathrm{x}−\mathrm{2}\right)^{\mathrm{2}} −\mathrm{2}>\mathrm{0}\:\Rightarrow\left(\mathrm{x}−\mathrm{2}−\sqrt{\mathrm{2}}\right)\left(\mathrm{x}−\mathrm{2}+\sqrt{\mathrm{2}}\right)>\mathrm{0}\:\Rightarrow \\ $$$$\left.\mathrm{x}\in\right]−\infty,\mathrm{2}−\sqrt{\mathrm{2}}\left[\cup\right]\mathrm{2}+\sqrt{\mathrm{2}},+\infty\left[\right. \\ $$$$\mathrm{ln}\left(\mathrm{x}^{\mathrm{2}} −\mathrm{4x}+\mathrm{3}\right)<\mathrm{0}\:\Rightarrow\mathrm{x}^{\mathrm{2}} −\mathrm{4x}+\mathrm{3}<\mathrm{1}\:\Rightarrow\mathrm{x}^{\mathrm{2}} −\mathrm{4x}+\mathrm{2}<\mathrm{0}\:\Rightarrow \\ $$$$\left.\right]\mathrm{2}−\sqrt{\mathrm{2}},\mathrm{2}+\sqrt{\mathrm{2}}\left[\:\mathrm{the}\:\mathrm{problem}\:\mathrm{lead}\:\mathrm{to}\:\mathrm{find}\:\mathrm{sgn}\:\mathrm{of}\:\left(\mathrm{x}^{\mathrm{2}} −\mathrm{6x}+\mathrm{4}\right)\mathrm{ln}\left(\mathrm{x}^{\mathrm{2}} −\mathrm{4x}+\mathrm{3}\right)\right. \\ $$$$…\mathrm{be}\:\mathrm{continued}… \\ $$
Answered by MJS_new last updated on 24/Jan/21
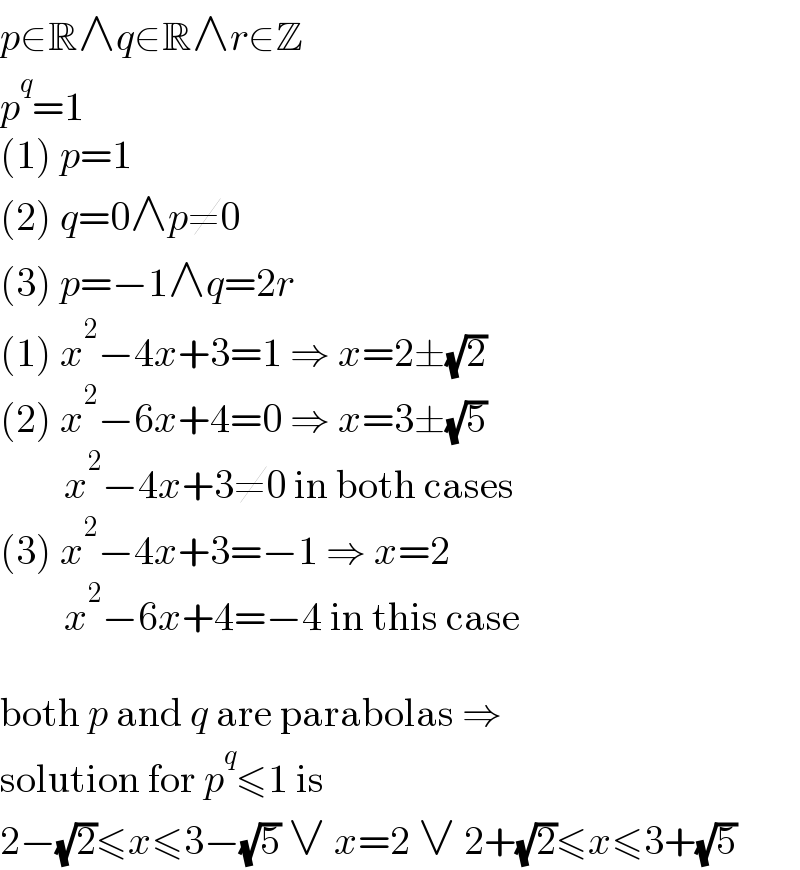
$${p}\in\mathbb{R}\wedge{q}\in\mathbb{R}\wedge{r}\in\mathbb{Z} \\ $$$${p}^{{q}} =\mathrm{1} \\ $$$$\left(\mathrm{1}\right)\:{p}=\mathrm{1} \\ $$$$\left(\mathrm{2}\right)\:{q}=\mathrm{0}\wedge{p}\neq\mathrm{0} \\ $$$$\left(\mathrm{3}\right)\:{p}=−\mathrm{1}\wedge{q}=\mathrm{2}{r} \\ $$$$\left(\mathrm{1}\right)\:{x}^{\mathrm{2}} −\mathrm{4}{x}+\mathrm{3}=\mathrm{1}\:\Rightarrow\:{x}=\mathrm{2}\pm\sqrt{\mathrm{2}} \\ $$$$\left(\mathrm{2}\right)\:{x}^{\mathrm{2}} −\mathrm{6}{x}+\mathrm{4}=\mathrm{0}\:\Rightarrow\:{x}=\mathrm{3}\pm\sqrt{\mathrm{5}} \\ $$$$\:\:\:\:\:\:\:\:{x}^{\mathrm{2}} −\mathrm{4}{x}+\mathrm{3}\neq\mathrm{0}\:\mathrm{in}\:\mathrm{both}\:\mathrm{cases} \\ $$$$\left(\mathrm{3}\right)\:{x}^{\mathrm{2}} −\mathrm{4}{x}+\mathrm{3}=−\mathrm{1}\:\Rightarrow\:{x}=\mathrm{2} \\ $$$$\:\:\:\:\:\:\:\:{x}^{\mathrm{2}} −\mathrm{6}{x}+\mathrm{4}=−\mathrm{4}\:\mathrm{in}\:\mathrm{this}\:\mathrm{case} \\ $$$$ \\ $$$$\mathrm{both}\:{p}\:\mathrm{and}\:{q}\:\mathrm{are}\:\mathrm{parabolas}\:\Rightarrow \\ $$$$\mathrm{solution}\:\mathrm{for}\:{p}^{{q}} \leqslant\mathrm{1}\:\mathrm{is} \\ $$$$\mathrm{2}−\sqrt{\mathrm{2}}\leqslant{x}\leqslant\mathrm{3}−\sqrt{\mathrm{5}}\:\vee\:{x}=\mathrm{2}\:\vee\:\mathrm{2}+\sqrt{\mathrm{2}}\leqslant{x}\leqslant\mathrm{3}+\sqrt{\mathrm{5}} \\ $$
