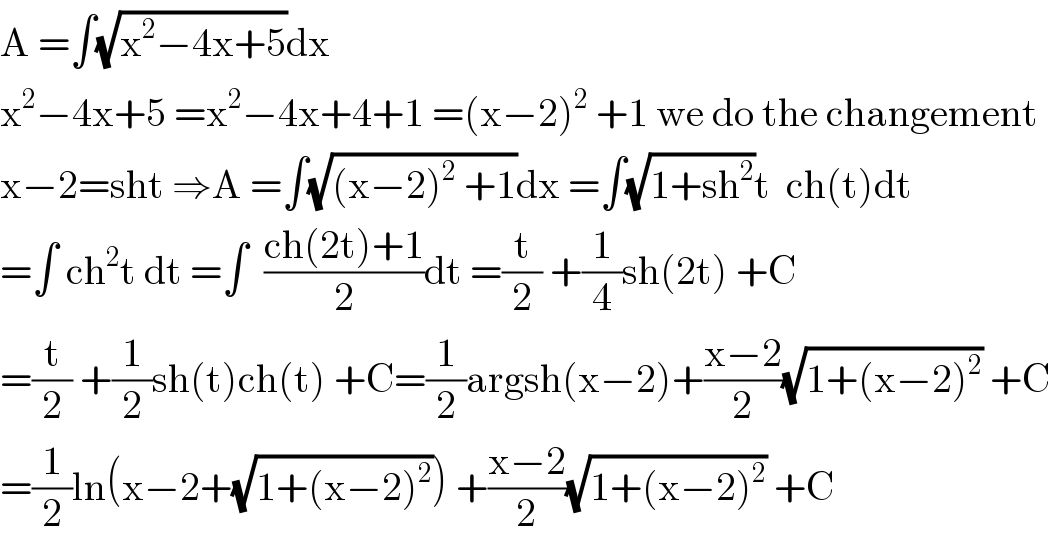x-2-4x-5-dx-

Question Number 123234 by benjo_mathlover last updated on 24/Nov/20

$$\:\:\int\:\sqrt{{x}^{\mathrm{2}} −\mathrm{4}{x}+\mathrm{5}}\:{dx}\: \\ $$

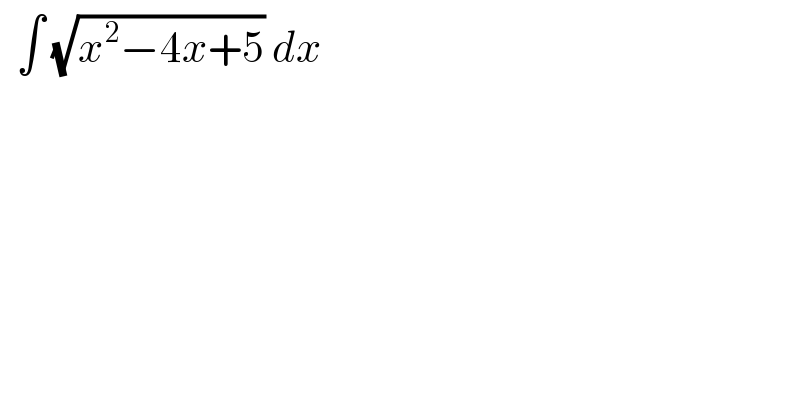
Commented by liberty last updated on 24/Nov/20

Answered by MJS_new last updated on 24/Nov/20

∫(√(x^2 −4x+5))dx= [t=x−2+(√(x^2 −4x+5)) → dx=((√(x^2 −4x+5))/(x−2+(√(x^2 −4x+5))))] [use x=((t^2 +4t−1)/(2t))∧t>0] =∫(((t^2 +1)^2 )/(4t^3 ))dt=∫((t/4)+(1/(2t))+(1/(4t^3 )))dt= =((t^4 −1)/(8t^2 ))+(1/2)ln t = =((x−2)/2)(√(x^2 −4x+5))+(1/2)ln (x−2+(√(x^2 −4x+5))) +C

$$\int\sqrt{{x}^{\mathrm{2}} −\mathrm{4}{x}+\mathrm{5}}{dx}= \\ $$$$\:\:\:\:\:\left[{t}={x}−\mathrm{2}+\sqrt{{x}^{\mathrm{2}} −\mathrm{4}{x}+\mathrm{5}}\:\rightarrow\:{dx}=\frac{\sqrt{{x}^{\mathrm{2}} −\mathrm{4}{x}+\mathrm{5}}}{{x}−\mathrm{2}+\sqrt{{x}^{\mathrm{2}} −\mathrm{4}{x}+\mathrm{5}}}\right] \\ $$$$\:\:\:\:\:\left[\mathrm{use}\:{x}=\frac{{t}^{\mathrm{2}} +\mathrm{4}{t}−\mathrm{1}}{\mathrm{2}{t}}\wedge{t}>\mathrm{0}\right] \\ $$$$=\int\frac{\left({t}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }{\mathrm{4}{t}^{\mathrm{3}} }{dt}=\int\left(\frac{{t}}{\mathrm{4}}+\frac{\mathrm{1}}{\mathrm{2}{t}}+\frac{\mathrm{1}}{\mathrm{4}{t}^{\mathrm{3}} }\right){dt}= \\ $$$$=\frac{{t}^{\mathrm{4}} −\mathrm{1}}{\mathrm{8}{t}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\:{t}\:= \\ $$$$=\frac{{x}−\mathrm{2}}{\mathrm{2}}\sqrt{{x}^{\mathrm{2}} −\mathrm{4}{x}+\mathrm{5}}+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\:\left({x}−\mathrm{2}+\sqrt{{x}^{\mathrm{2}} −\mathrm{4}{x}+\mathrm{5}}\right)\:+{C} \\ $$

Answered by Dwaipayan Shikari last updated on 24/Nov/20

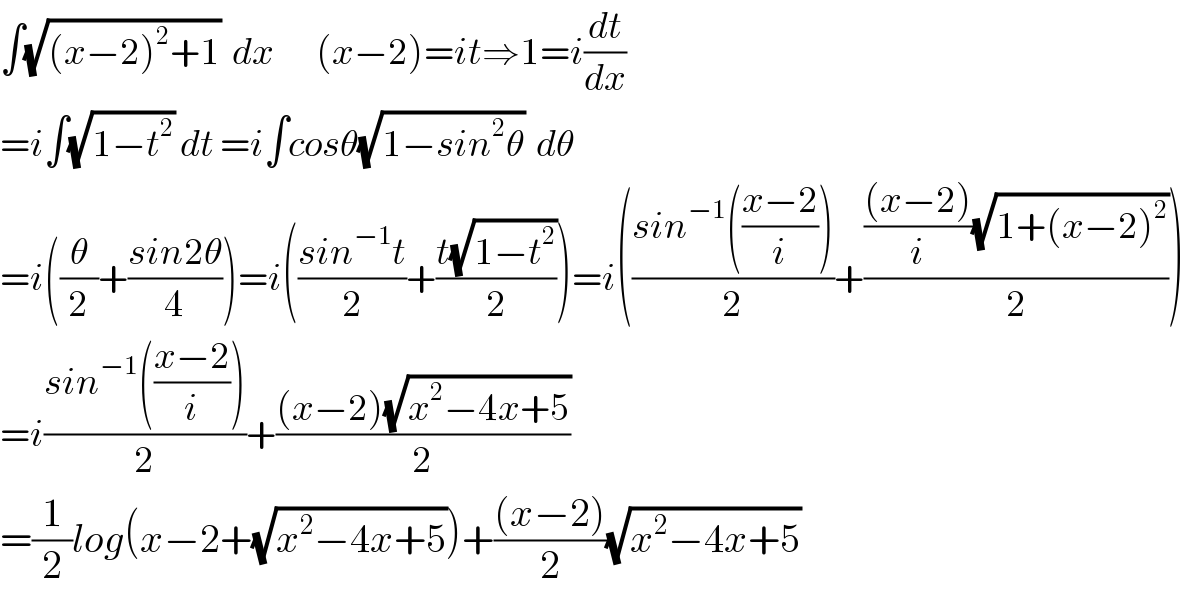
∫(√((x−2)^2 +1)) dx (x−2)=it⇒1=i(dt/dx) =i∫(√(1−t^2 )) dt =i∫cosθ(√(1−sin^2 θ)) dθ =i((θ/2)+((sin2θ)/4))=i(((sin^(−1) t)/2)+((t(√(1−t^2 )))/2))=i(((sin^(−1) (((x−2)/i)))/2)+(((((x−2))/i)(√(1+(x−2)^2 )))/2)) =i((sin^(−1) (((x−2)/i)))/2)+(((x−2)(√(x^2 −4x+5)))/2) =(1/2)log(x−2+(√(x^2 −4x+5)))+(((x−2))/2)(√(x^2 −4x+5))

$$\int\sqrt{\left({x}−\mathrm{2}\right)^{\mathrm{2}} +\mathrm{1}}\:\:{dx}\:\:\:\:\:\:\:\left({x}−\mathrm{2}\right)={it}\Rightarrow\mathrm{1}={i}\frac{{dt}}{{dx}}\: \\ $$$$={i}\int\sqrt{\mathrm{1}−{t}^{\mathrm{2}} }\:{dt}\:={i}\int{cos}\theta\sqrt{\mathrm{1}−{sin}^{\mathrm{2}} \theta}\:\:{d}\theta \\ $$$$={i}\left(\frac{\theta}{\mathrm{2}}+\frac{{sin}\mathrm{2}\theta}{\mathrm{4}}\right)={i}\left(\frac{{sin}^{−\mathrm{1}} {t}}{\mathrm{2}}+\frac{{t}\sqrt{\mathrm{1}−{t}^{\mathrm{2}} }}{\mathrm{2}}\right)={i}\left(\frac{{sin}^{−\mathrm{1}} \left(\frac{{x}−\mathrm{2}}{{i}}\right)}{\mathrm{2}}+\frac{\frac{\left({x}−\mathrm{2}\right)}{{i}}\sqrt{\mathrm{1}+\left({x}−\mathrm{2}\right)^{\mathrm{2}} }}{\mathrm{2}}\right) \\ $$$$={i}\frac{{sin}^{−\mathrm{1}} \left(\frac{{x}−\mathrm{2}}{{i}}\right)}{\mathrm{2}}+\frac{\left({x}−\mathrm{2}\right)\sqrt{{x}^{\mathrm{2}} −\mathrm{4}{x}+\mathrm{5}}}{\mathrm{2}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}{log}\left({x}−\mathrm{2}+\sqrt{{x}^{\mathrm{2}} −\mathrm{4}{x}+\mathrm{5}}\right)+\frac{\left({x}−\mathrm{2}\right)}{\mathrm{2}}\sqrt{{x}^{\mathrm{2}} −\mathrm{4}{x}+\mathrm{5}} \\ $$

Commented by Dwaipayan Shikari last updated on 24/Nov/20

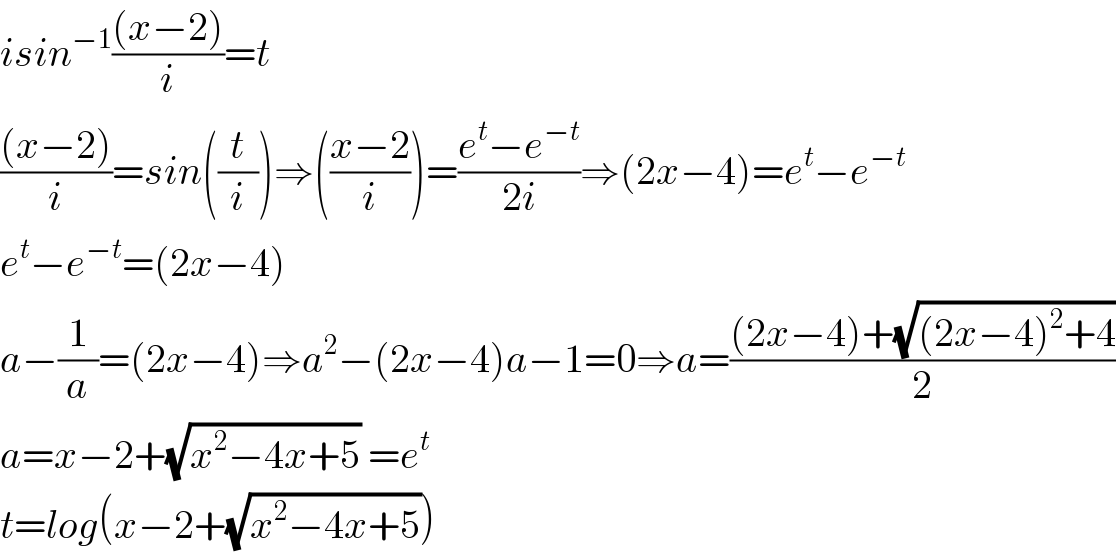
isin^(−1) (((x−2))/i)=t (((x−2))/i)=sin((t/i))⇒(((x−2)/i))=((e^t −e^(−t) )/(2i))⇒(2x−4)=e^t −e^(−t) e^t −e^(−t) =(2x−4) a−(1/a)=(2x−4)⇒a^2 −(2x−4)a−1=0⇒a=(((2x−4)+(√((2x−4)^2 +4)))/2) a=x−2+(√(x^2 −4x+5)) =e^t t=log(x−2+(√(x^2 −4x+5)))

$${isin}^{−\mathrm{1}} \frac{\left({x}−\mathrm{2}\right)}{{i}}={t} \\ $$$$\frac{\left({x}−\mathrm{2}\right)}{{i}}={sin}\left(\frac{{t}}{{i}}\right)\Rightarrow\left(\frac{{x}−\mathrm{2}}{{i}}\right)=\frac{{e}^{{t}} −{e}^{−{t}} }{\mathrm{2}{i}}\Rightarrow\left(\mathrm{2}{x}−\mathrm{4}\right)={e}^{{t}} −{e}^{−{t}} \\ $$$${e}^{{t}} −{e}^{−{t}} =\left(\mathrm{2}{x}−\mathrm{4}\right) \\ $$$${a}−\frac{\mathrm{1}}{{a}}=\left(\mathrm{2}{x}−\mathrm{4}\right)\Rightarrow{a}^{\mathrm{2}} −\left(\mathrm{2}{x}−\mathrm{4}\right){a}−\mathrm{1}=\mathrm{0}\Rightarrow{a}=\frac{\left(\mathrm{2}{x}−\mathrm{4}\right)+\sqrt{\left(\mathrm{2}{x}−\mathrm{4}\right)^{\mathrm{2}} +\mathrm{4}}}{\mathrm{2}} \\ $$$${a}={x}−\mathrm{2}+\sqrt{{x}^{\mathrm{2}} −\mathrm{4}{x}+\mathrm{5}}\:={e}^{{t}} \\ $$$${t}={log}\left({x}−\mathrm{2}+\sqrt{{x}^{\mathrm{2}} −\mathrm{4}{x}+\mathrm{5}}\right) \\ $$

Answered by mathmax by abdo last updated on 24/Nov/20

A =∫(√(x^2 −4x+5))dx x^2 −4x+5 =x^2 −4x+4+1 =(x−2)^2 +1 we do the changement x−2=sht ⇒A =∫(√((x−2)^2 +1))dx =∫(√(1+sh^2 ))t ch(t)dt =∫ ch^2 t dt =∫ ((ch(2t)+1)/2)dt =(t/2) +(1/4)sh(2t) +C =(t/2) +(1/2)sh(t)ch(t) +C=(1/2)argsh(x−2)+((x−2)/2)(√(1+(x−2)^2 )) +C =(1/2)ln(x−2+(√(1+(x−2)^2 ))) +((x−2)/2)(√(1+(x−2)^2 )) +C

$$\mathrm{A}\:=\int\sqrt{\mathrm{x}^{\mathrm{2}} −\mathrm{4x}+\mathrm{5}}\mathrm{dx} \\ $$$$\mathrm{x}^{\mathrm{2}} −\mathrm{4x}+\mathrm{5}\:=\mathrm{x}^{\mathrm{2}} −\mathrm{4x}+\mathrm{4}+\mathrm{1}\:=\left(\mathrm{x}−\mathrm{2}\right)^{\mathrm{2}} \:+\mathrm{1}\:\mathrm{we}\:\mathrm{do}\:\mathrm{the}\:\mathrm{changement} \\ $$$$\mathrm{x}−\mathrm{2}=\mathrm{sht}\:\Rightarrow\mathrm{A}\:=\int\sqrt{\left(\mathrm{x}−\mathrm{2}\right)^{\mathrm{2}} \:+\mathrm{1}}\mathrm{dx}\:=\int\sqrt{\mathrm{1}+\mathrm{sh}^{\mathrm{2}} }\mathrm{t}\:\:\mathrm{ch}\left(\mathrm{t}\right)\mathrm{dt} \\ $$$$=\int\:\mathrm{ch}^{\mathrm{2}} \mathrm{t}\:\mathrm{dt}\:=\int\:\:\frac{\mathrm{ch}\left(\mathrm{2t}\right)+\mathrm{1}}{\mathrm{2}}\mathrm{dt}\:=\frac{\mathrm{t}}{\mathrm{2}}\:+\frac{\mathrm{1}}{\mathrm{4}}\mathrm{sh}\left(\mathrm{2t}\right)\:+\mathrm{C} \\ $$$$=\frac{\mathrm{t}}{\mathrm{2}}\:+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sh}\left(\mathrm{t}\right)\mathrm{ch}\left(\mathrm{t}\right)\:+\mathrm{C}=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{argsh}\left(\mathrm{x}−\mathrm{2}\right)+\frac{\mathrm{x}−\mathrm{2}}{\mathrm{2}}\sqrt{\mathrm{1}+\left(\mathrm{x}−\mathrm{2}\right)^{\mathrm{2}} }\:+\mathrm{C} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\left(\mathrm{x}−\mathrm{2}+\sqrt{\mathrm{1}+\left(\mathrm{x}−\mathrm{2}\right)^{\mathrm{2}} }\right)\:+\frac{\mathrm{x}−\mathrm{2}}{\mathrm{2}}\sqrt{\mathrm{1}+\left(\mathrm{x}−\mathrm{2}\right)^{\mathrm{2}} }\:+\mathrm{C} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply