Question Number 185127 by Shrinava last updated on 17/Jan/23
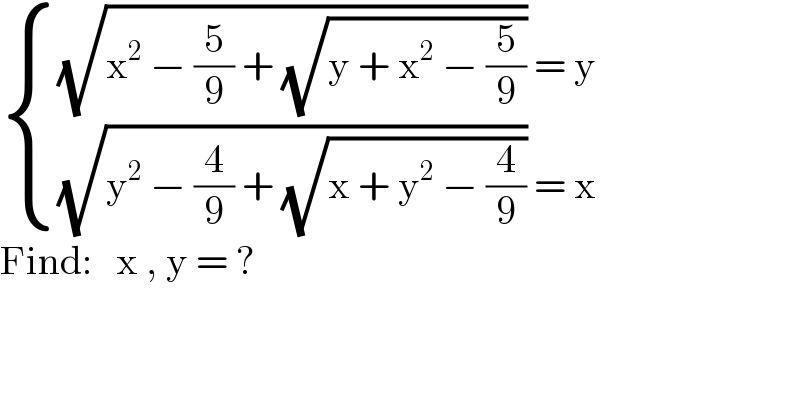
$$\begin{cases}{\sqrt{\mathrm{x}^{\mathrm{2}} \:−\:\frac{\mathrm{5}}{\mathrm{9}}\:+\:\sqrt{\mathrm{y}\:+\:\mathrm{x}^{\mathrm{2}} \:−\:\frac{\mathrm{5}}{\mathrm{9}}}}\:=\:\mathrm{y}}\\{\sqrt{\mathrm{y}^{\mathrm{2}} \:−\:\frac{\mathrm{4}}{\mathrm{9}}\:+\:\sqrt{\mathrm{x}\:+\:\mathrm{y}^{\mathrm{2}} \:−\:\frac{\mathrm{4}}{\mathrm{9}}}}\:=\:\mathrm{x}}\end{cases} \\ $$$$\mathrm{Find}:\:\:\:\mathrm{x}\:,\:\mathrm{y}\:=\:? \\ $$
Commented by Frix last updated on 17/Jan/23

$${x}=\frac{\mathrm{5}}{\mathrm{9}}\wedge{y}=\frac{\mathrm{4}}{\mathrm{9}} \\ $$
Commented by Shrinava last updated on 17/Jan/23

$$\mathrm{solution}\:\mathrm{please}\:\mathrm{dear}\:\mathrm{ser} \\ $$
Commented by Frix last updated on 17/Jan/23

$$\mathrm{The}\:\mathrm{easiest}\:\mathrm{way}\:\mathrm{is}\:\mathrm{to}\:\mathrm{set}\:{y}={px} \\ $$$$\mathrm{Squaring}\:\mathrm{and}\:\mathrm{transforming}\:\mathrm{both}\:\mathrm{equations} \\ $$$$\mathrm{two}\:\mathrm{times}\:\mathrm{and}\:\mathrm{then}\:\mathrm{subtracting}\:\mathrm{leads}\:\mathrm{to} \\ $$$$\mathrm{a}\:\mathrm{quadratic}\:\mathrm{equation}\:\mathrm{which}\:\mathrm{is}\:\mathrm{easy}\:\mathrm{to}\:\mathrm{solve} \\ $$$$\mathrm{for}\:{p}\:\mathrm{or}\:{x}. \\ $$$$\mathrm{Then}\:\mathrm{we}\:\mathrm{get}\:\mathrm{4}\:\mathrm{solutions}\:\mathrm{which}\:\mathrm{we}\:\mathrm{must} \\ $$$$\mathrm{check}\:\Rightarrow\:\mathrm{only}\:\mathrm{1}\:\mathrm{solution}\:\mathrm{is}\:\mathrm{valid}. \\ $$
