Question Number 161966 by amin96 last updated on 24/Dec/21
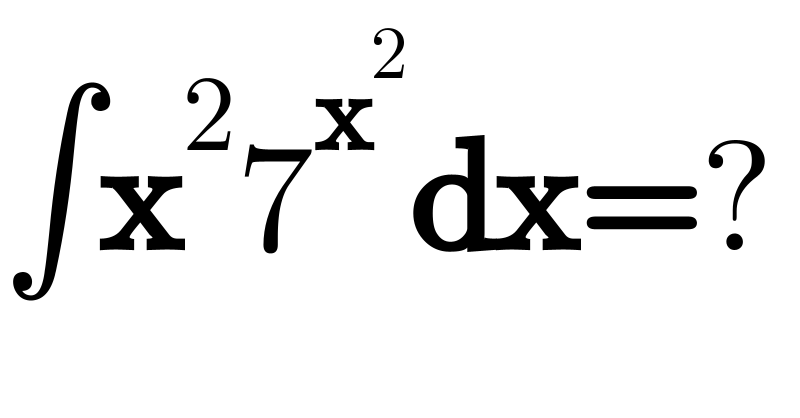
$$\int\boldsymbol{\mathrm{x}}^{\mathrm{2}} \mathrm{7}^{\boldsymbol{\mathrm{x}}^{\mathrm{2}} } \boldsymbol{\mathrm{dx}}=? \\ $$
Answered by Ar Brandon last updated on 25/Dec/21
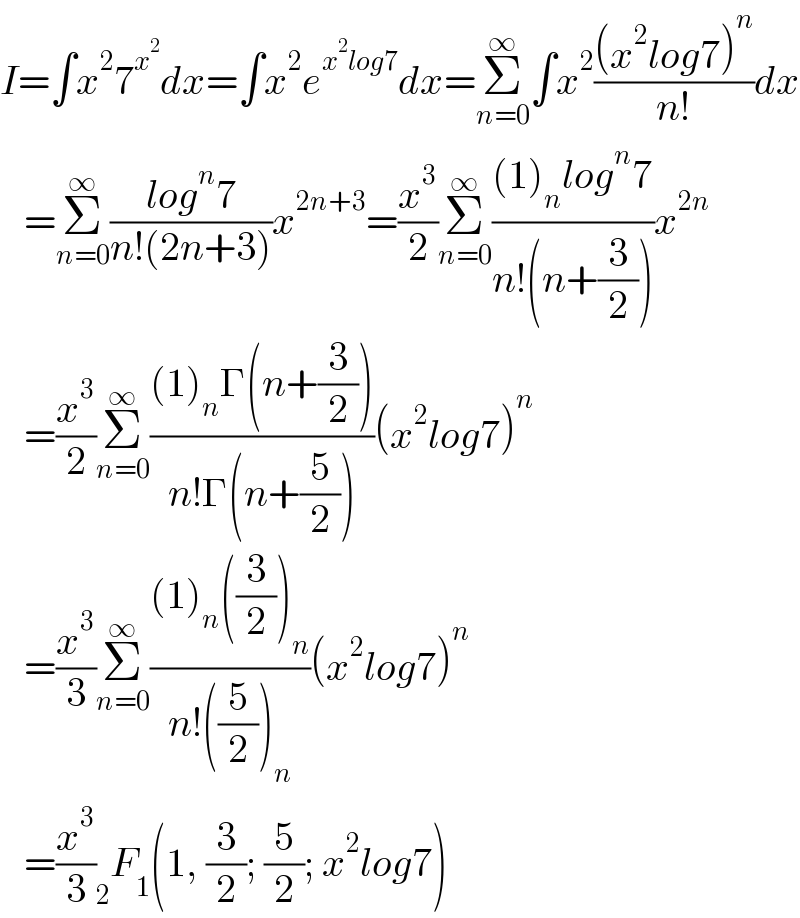
$${I}=\int{x}^{\mathrm{2}} \mathrm{7}^{{x}^{\mathrm{2}} } {dx}=\int{x}^{\mathrm{2}} {e}^{{x}^{\mathrm{2}} {log}\mathrm{7}} {dx}=\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\int{x}^{\mathrm{2}} \frac{\left({x}^{\mathrm{2}} {log}\mathrm{7}\right)^{{n}} }{{n}!}{dx} \\ $$$$\:\:\:=\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{{log}^{{n}} \mathrm{7}}{{n}!\left(\mathrm{2}{n}+\mathrm{3}\right)}{x}^{\mathrm{2}{n}+\mathrm{3}} =\frac{{x}^{\mathrm{3}} }{\mathrm{2}}\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(\mathrm{1}\right)_{{n}} {log}^{{n}} \mathrm{7}}{{n}!\left({n}+\frac{\mathrm{3}}{\mathrm{2}}\right)}{x}^{\mathrm{2}{n}} \\ $$$$\:\:\:=\frac{{x}^{\mathrm{3}} }{\mathrm{2}}\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(\mathrm{1}\right)_{{n}} \Gamma\left({n}+\frac{\mathrm{3}}{\mathrm{2}}\right)}{{n}!\Gamma\left({n}+\frac{\mathrm{5}}{\mathrm{2}}\right)}\left({x}^{\mathrm{2}} {log}\mathrm{7}\right)^{{n}} \\ $$$$\:\:\:=\frac{{x}^{\mathrm{3}} }{\mathrm{3}}\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(\mathrm{1}\right)_{{n}} \left(\frac{\mathrm{3}}{\mathrm{2}}\right)_{{n}} }{{n}!\left(\frac{\mathrm{5}}{\mathrm{2}}\right)_{{n}} }\left({x}^{\mathrm{2}} {log}\mathrm{7}\right)^{{n}} \\ $$$$\:\:\:=\frac{{x}^{\mathrm{3}} }{\mathrm{3}}\underset{\mathrm{2}} {\:}{F}_{\mathrm{1}} \left(\mathrm{1},\:\frac{\mathrm{3}}{\mathrm{2}};\:\frac{\mathrm{5}}{\mathrm{2}};\:{x}^{\mathrm{2}} {log}\mathrm{7}\right) \\ $$
Commented by amin96 last updated on 25/Dec/21

$${what}\:{is}\:{F}_{\mathrm{1}} ?? \\ $$
