Question Number 55195 by behi83417@gmail.com last updated on 19/Feb/19

$$\boldsymbol{\mathrm{x}}^{\mathrm{2}} +\boldsymbol{\mathrm{ax}}+\sqrt{\mathrm{2}}\boldsymbol{\mathrm{b}}=\mathrm{0},\boldsymbol{\mathrm{has}}\:\mathrm{2}\:\boldsymbol{\mathrm{roots}}:\boldsymbol{\mathrm{c}}\:\boldsymbol{\mathrm{and}}\:\boldsymbol{\mathrm{d}},\boldsymbol{\mathrm{also}} \\ $$$$\boldsymbol{\mathrm{x}}^{\mathrm{2}} +\boldsymbol{\mathrm{cx}}+\sqrt{\mathrm{2}}\boldsymbol{\mathrm{d}}=\mathrm{0},\boldsymbol{\mathrm{has}}\:\mathrm{2}\:\boldsymbol{\mathrm{roots}}:\boldsymbol{\mathrm{a}}\:\boldsymbol{\mathrm{and}}\:\boldsymbol{\mathrm{b}}.\boldsymbol{\mathrm{such}} \\ $$$$\boldsymbol{\mathrm{that}}:\boldsymbol{\mathrm{a}},\:\boldsymbol{\mathrm{b}},\:\boldsymbol{\mathrm{c}},\:\boldsymbol{\mathrm{d}},\boldsymbol{\mathrm{are}}\:\boldsymbol{\mathrm{defferent}}\:\boldsymbol{\mathrm{non}}\:\boldsymbol{\mathrm{zero}}\: \\ $$$$\boldsymbol{\mathrm{numbers}}. \\ $$$$\boldsymbol{\mathrm{find}}\:\boldsymbol{\mathrm{possible}}\:\boldsymbol{\mathrm{value}}\left(\boldsymbol{\mathrm{s}}\right)\:\boldsymbol{\mathrm{for}}:\boldsymbol{\mathrm{a}}^{\mathrm{2}} +\boldsymbol{\mathrm{b}}^{\mathrm{2}} +\boldsymbol{\mathrm{c}}^{\mathrm{2}} +\boldsymbol{\mathrm{d}}^{\mathrm{2}} . \\ $$
Answered by behi83417@gmail.com last updated on 19/Feb/19
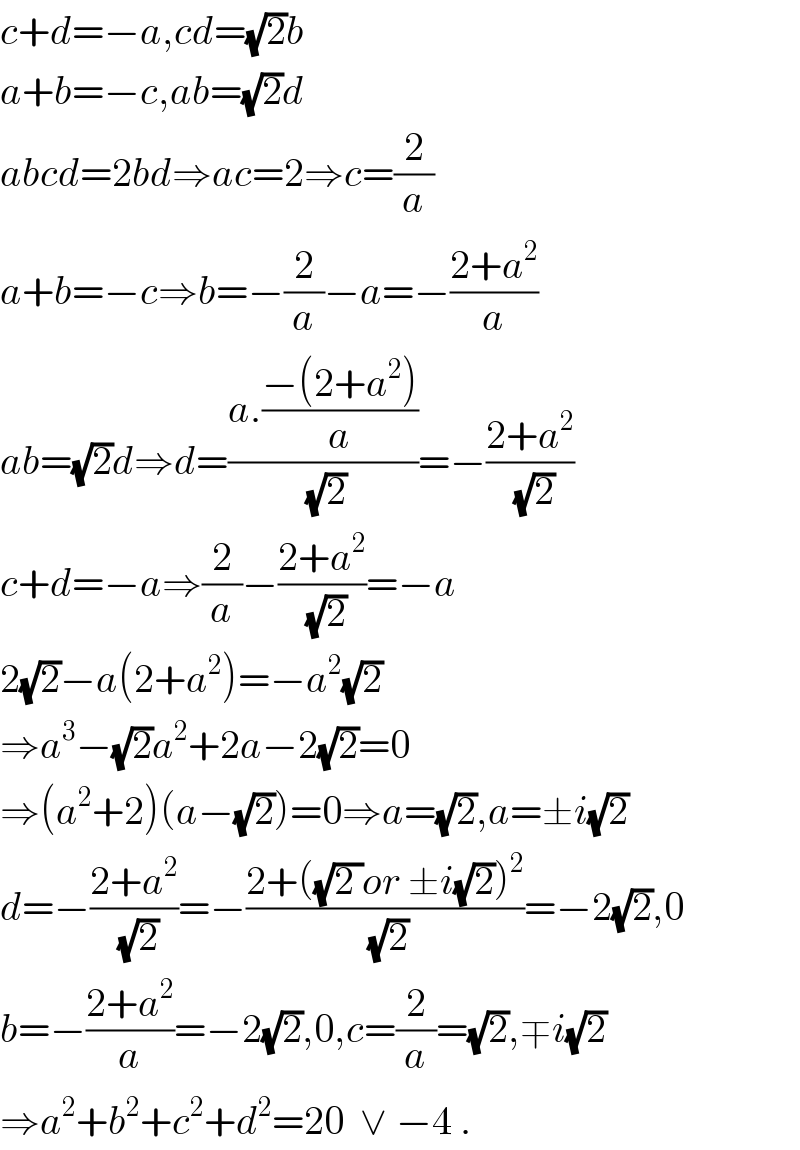
$${c}+{d}=−{a},{cd}=\sqrt{\mathrm{2}}{b} \\ $$$${a}+{b}=−{c},{ab}=\sqrt{\mathrm{2}}{d} \\ $$$${abcd}=\mathrm{2}{bd}\Rightarrow{ac}=\mathrm{2}\Rightarrow{c}=\frac{\mathrm{2}}{{a}} \\ $$$${a}+{b}=−{c}\Rightarrow{b}=−\frac{\mathrm{2}}{{a}}−{a}=−\frac{\mathrm{2}+{a}^{\mathrm{2}} }{{a}} \\ $$$${ab}=\sqrt{\mathrm{2}}{d}\Rightarrow{d}=\frac{{a}.\frac{−\left(\mathrm{2}+{a}^{\mathrm{2}} \right)}{{a}}}{\:\sqrt{\mathrm{2}}}=−\frac{\mathrm{2}+{a}^{\mathrm{2}} }{\:\sqrt{\mathrm{2}}} \\ $$$${c}+{d}=−{a}\Rightarrow\frac{\mathrm{2}}{{a}}−\frac{\mathrm{2}+{a}^{\mathrm{2}} }{\:\sqrt{\mathrm{2}}}=−{a} \\ $$$$\mathrm{2}\sqrt{\mathrm{2}}−{a}\left(\mathrm{2}+{a}^{\mathrm{2}} \right)=−{a}^{\mathrm{2}} \sqrt{\mathrm{2}} \\ $$$$\Rightarrow{a}^{\mathrm{3}} −\sqrt{\mathrm{2}}{a}^{\mathrm{2}} +\mathrm{2}{a}−\mathrm{2}\sqrt{\mathrm{2}}=\mathrm{0} \\ $$$$\Rightarrow\left({a}^{\mathrm{2}} +\mathrm{2}\right)\left({a}−\sqrt{\mathrm{2}}\right)=\mathrm{0}\Rightarrow{a}=\sqrt{\mathrm{2}},{a}=\pm{i}\sqrt{\mathrm{2}} \\ $$$${d}=−\frac{\mathrm{2}+{a}^{\mathrm{2}} }{\:\sqrt{\mathrm{2}}}=−\frac{\mathrm{2}+\left(\sqrt{\mathrm{2}\:}{or}\:\pm{i}\sqrt{\mathrm{2}}\right)^{\mathrm{2}} }{\:\sqrt{\mathrm{2}}}=−\mathrm{2}\sqrt{\mathrm{2}},\mathrm{0} \\ $$$${b}=−\frac{\mathrm{2}+{a}^{\mathrm{2}} }{{a}}=−\mathrm{2}\sqrt{\mathrm{2}},\mathrm{0},{c}=\frac{\mathrm{2}}{{a}}=\sqrt{\mathrm{2}},\mp{i}\sqrt{\mathrm{2}} \\ $$$$\Rightarrow{a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} +{d}^{\mathrm{2}} =\mathrm{20}\:\:\vee\:−\mathrm{4}\:. \\ $$
